小波认识的基础与分析

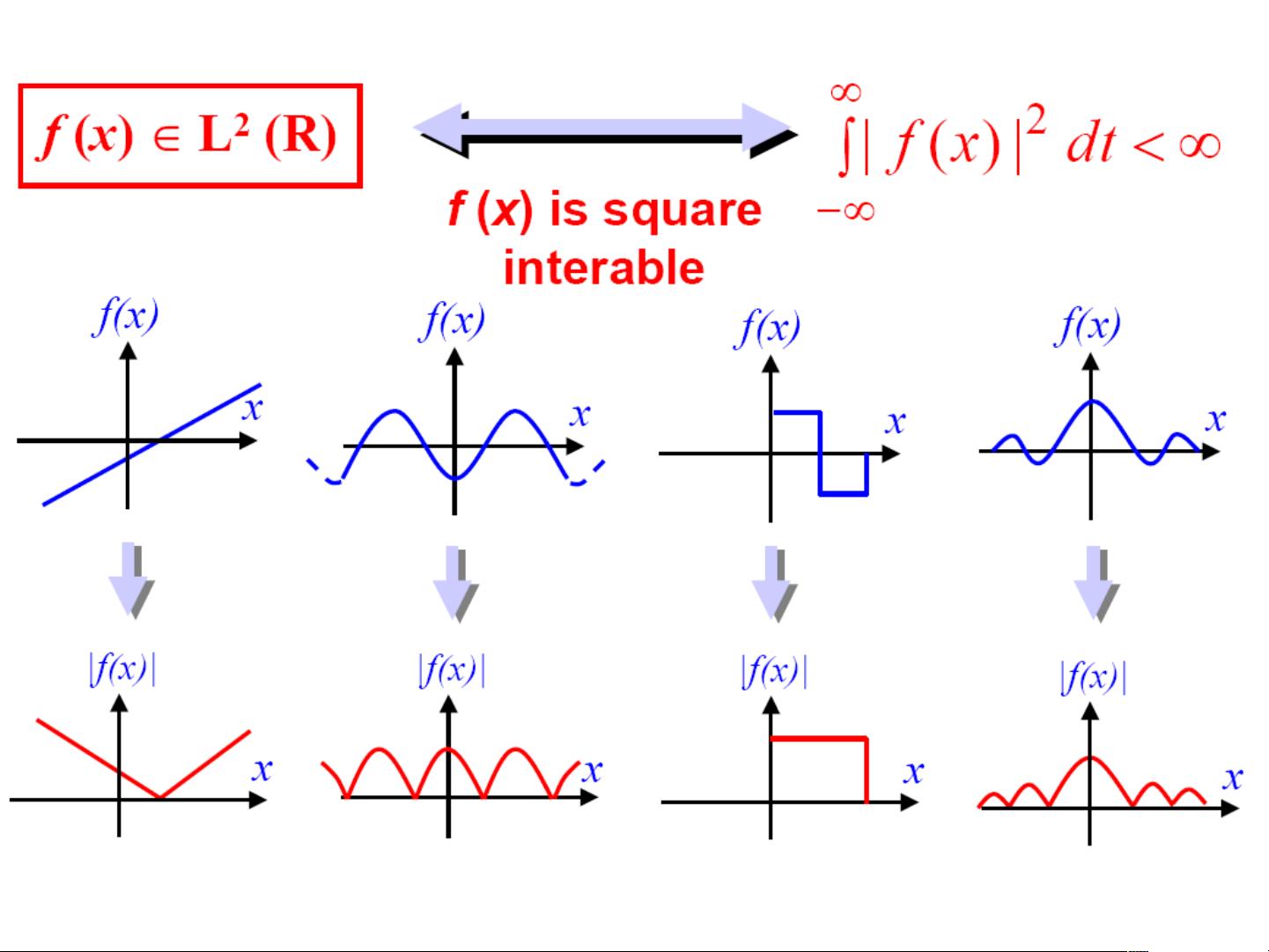
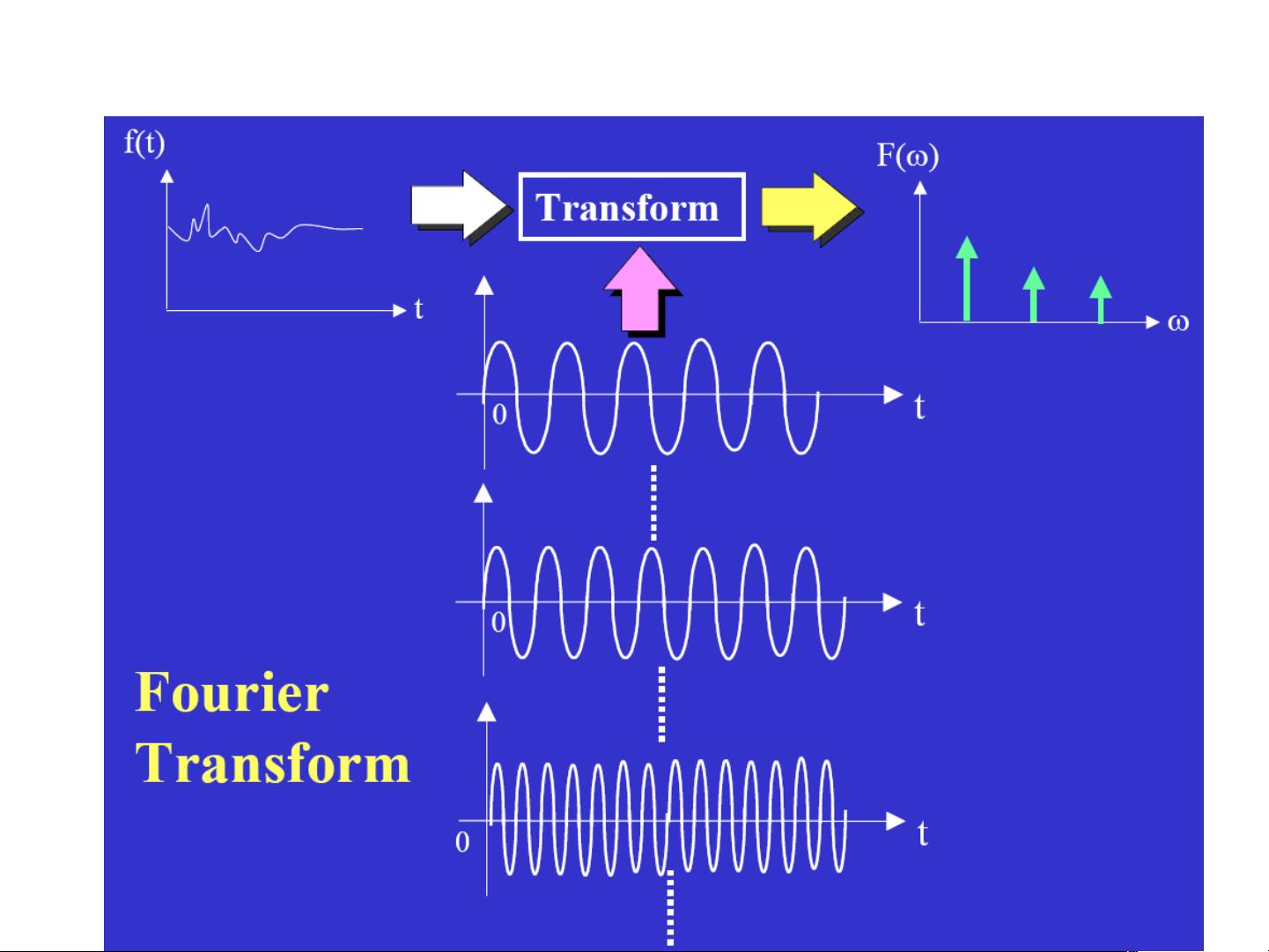
【小波分析基础】 小波分析是现代数学领域的一个重要分支，它结合了理论的深度与广泛应用，尤其在信号处理、图像分析、数据压缩、噪声去除等IT领域有着广泛的应用。小波分析的核心在于提供了一种同时在时间和频率上进行精细分析的方法，弥补了传统傅立叶变换只能在频域或时域分析信号的局限。 1. **信号的时频分析**： - 信号的时间特性与频率特性是描述信号本质的两个关键因素。它们之间的关系可以通过小波分析得到深入揭示。 - 传统的傅立叶变换虽然能给出信号的全局频谱信息，但无法体现信号在时间上的变化，即无法实现良好的时频局部化。 2. **窗口傅立叶变换（Gabor变换）**： - 它是傅立叶变换的一种变体，通过引入窗函数来限制分析的频率范围，从而获得信号在特定时间段内的频谱信息。 - 窗函数g(t)的宽度决定了分析的分辨率，窗口越窄，时间定位越精确，但频率分辨率降低。 3. 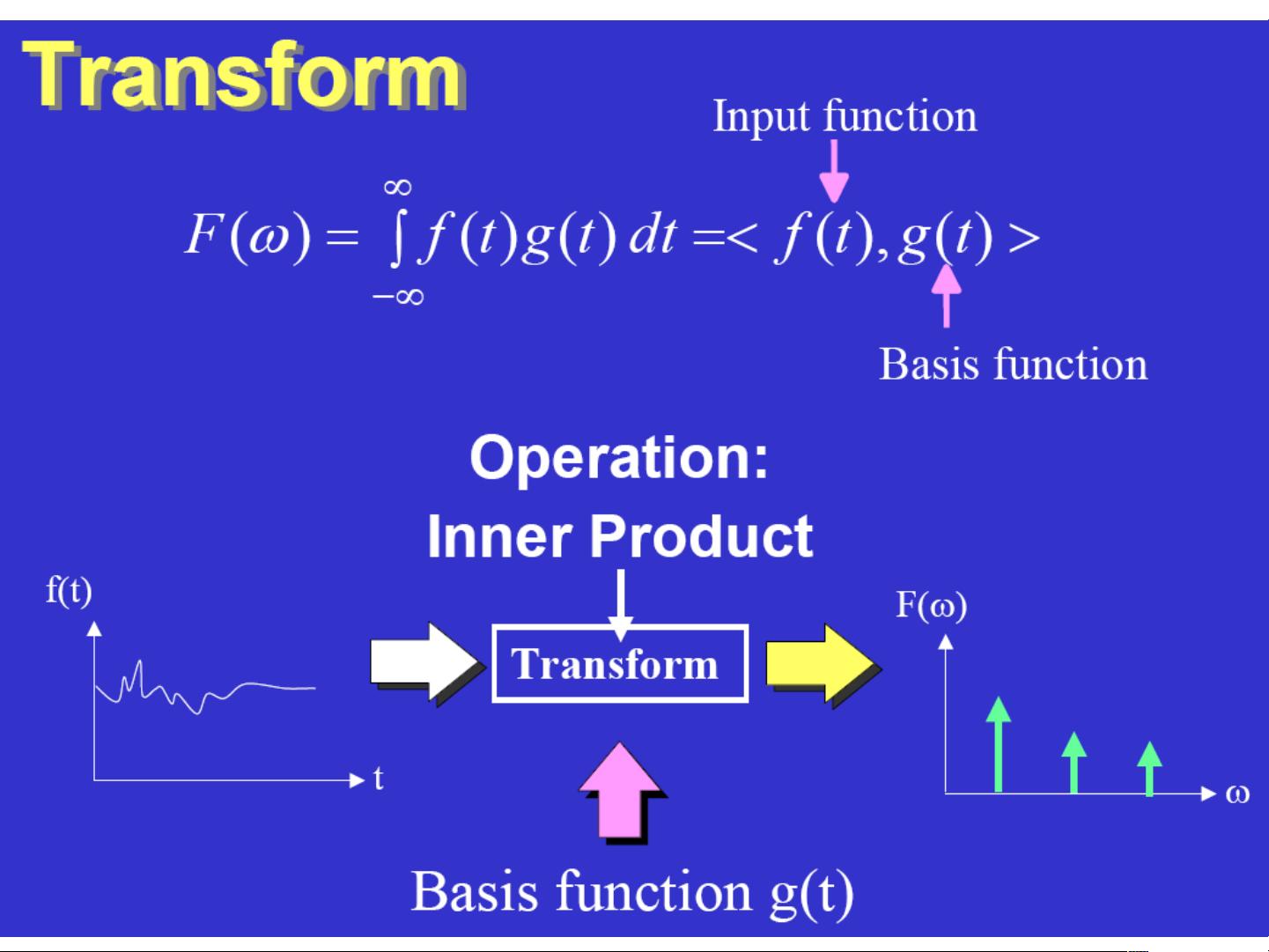**连续小波变换**： - 连续小波变换引入了小波函数ψ(t)，它是一种能在时间和频率上同时变化的基函数，可以更好地刻画信号的局部特征。 - 变换定义为f(t)与缩放和平移后的小波函数ψ(a, b)的卷积，其中a为尺度参数，b为时间平移参数。 - 母小波ψ(t)是所有小波的基础，通过调整a和b，可以生成不同尺度和位置的小波，用于分析信号的不同部分。 4. **离散化的小波变换**： - 为了实际计算，通常将尺度和时间参数离散化，形成离散小波变换，如Daubechies小波、Morlet小波等。 - 离散化过程中的小波函数选择需满足一定的条件，如容许条件，确保信号能被准确重构。 - 重构信号的小波函数应构成框架，满足框架条件，确保信号的唯一表示。 5. **标准正交小波基**： - 标准正交小波基的小波函数具有正交性，变换系数简洁且无冗余，便于信号性质的直观理解。 - 正交小波基与其对偶相同，简化了计算过程，且重构信号时只需通过小波系数的线性组合即可。 6. **多分辨分析（MRA）**： - MRA是构建正交小波基的重要工具，包括一维正交和双正交多分辨分析。 - Mallat算法是实现正交小波基的关键，通过迭代的滤波器组（低通滤波器和高通滤波器）构造尺度函数和小波函数。 - MRA的子空间序列满足单调性、逼近性、伸缩性、平移不变性和Riesz基存在性等条件，确保了小波分析的有效性和准确性。 小波分析不仅提供了对信号的时频局部化分析，而且在理论和技术上都具有很高的价值，是解决许多复杂IT问题的强大工具。通过小波变换，我们可以更深入地理解和处理各种信号，从而在通信、图像处理、音频分析等领域实现更精确的数据分析和信息提取。