郑大版的数值分析课件

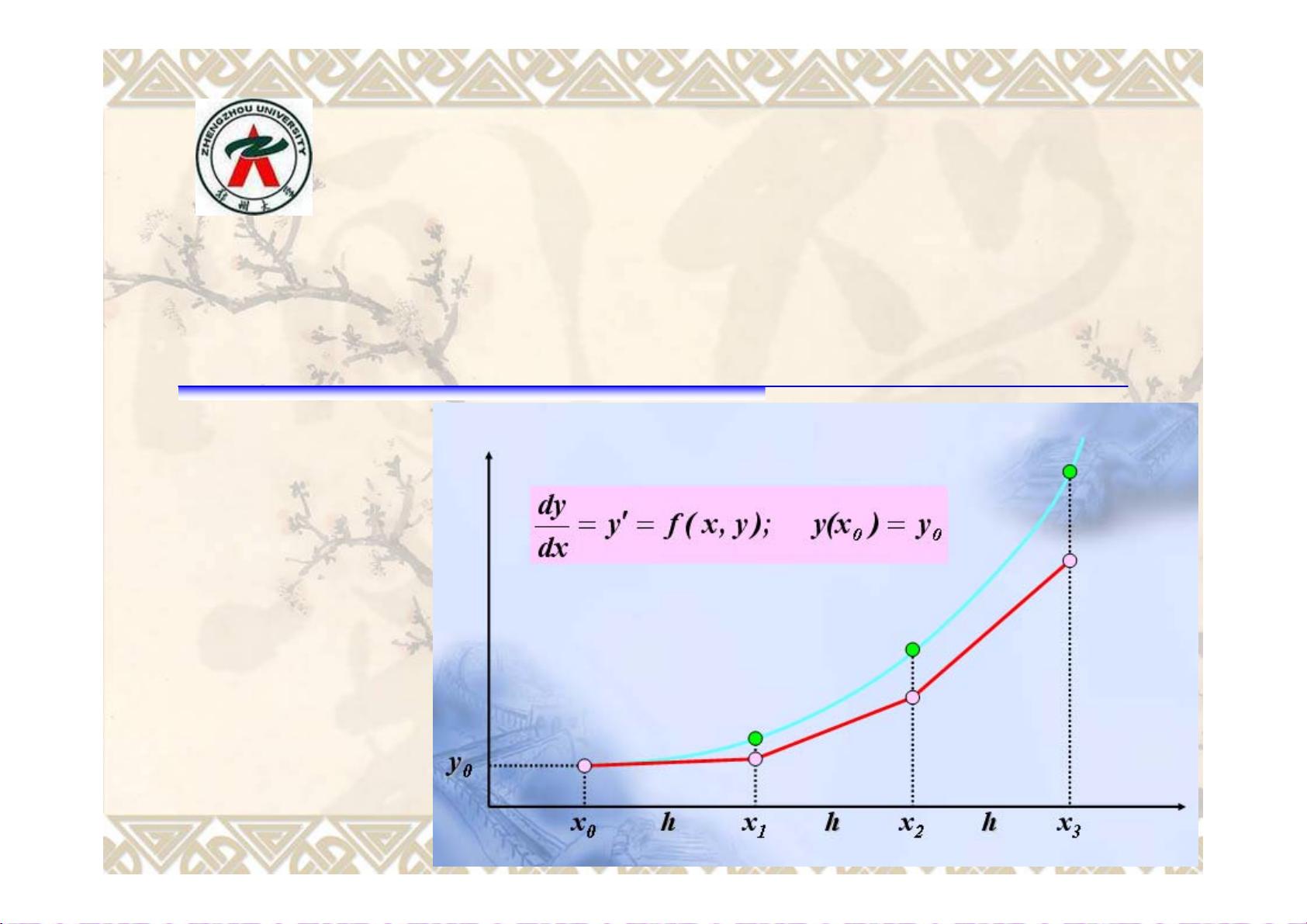
从给定的文件信息中，我们可以提取到关于数值分析中常微分方程数值解法的重要知识点，这些知识点主要集中在数值分析的第八章，由郑州大学于2009-2010学年第一学期教授给研究生。下面将详细阐述这些知识点。 ### 常微分方程数值解法概览 #### 引言 引言部分通过一个具体的实例——倒葫芦形状容器壁上的刻度问题，引入了常微分方程数值解法的概念。这个问题的核心在于解决非常规几何形状容器的容积刻度标注，特别是当容器的直径D随高度H变化而没有明确解析表达式时，如何通过数值方法找到体积V与高度x之间的函数关系。这涉及到微分方程的求解，尤其是当无法获得解析解时，采用数值方法来逼近解的重要性。 #### 欧拉(Euler)法 欧拉法是最基础的常微分方程数值解法之一，它通过泰勒级数展开的第一阶近似来逼近微分方程的解。该方法简单直观，但在实际应用中精度有限，尤其是在解的曲线变化较为剧烈的情况下。欧拉法的计算步骤包括设定一个足够小的时间步长，并基于当前时刻的解来预测下一个时刻的解。 #### 改进欧拉(Euler)方法 改进欧拉法，也被称为显式梯形法则，是对基本欧拉法的一种改进。它通过在欧拉法的基础上考虑当前和下一个时间步长的平均斜率，从而提高了解的精度。这种方法结合了前一步和预估的下一步的导数值，使得解的逼近更加准确。 #### 荣格-库塔(Runge-Kutta)方法 荣格-库塔方法是一种更高级的数值积分技术，尤其适用于解决复杂的常微分方程。第四阶荣格-库塔法是最常用的版本，它通过计算四个不同的斜率并取它们的加权平均来估计下一个时间步的解，从而大大提高了解的精度和稳定性。 #### 单步法的稳定性 单步法是指只依赖于前一步结果来计算下一步解的方法，如欧拉法、改进欧拉法和荣格-库塔法。这些方法的稳定性是关键，因为不稳定的算法可能导致解的振荡或发散。稳定性的分析通常涉及到特征根的判断，确保算法在长时间运行下仍能保持解的准确性。 #### 线性多步法 线性多步法是一类更复杂的数值解法，它不仅依赖于前一步的结果，还可能依赖于几步之前的解。这类方法能够提供更高的精度和更好的稳定性，但也可能带来更大的计算复杂度。常见的线性多步法包括亚当斯法和巴特森法。 ### 微分方程的基本概念 微分方程是一类涉及未知函数及其导数的方程，根据自变量的数量可分为常微分方程和偏微分方程。常微分方程处理的是单个自变量的情况，而偏微分方程处理的是多个自变量。微分方程根据未知函数的阶数又可以分为一阶、二阶等高阶微分方程，以及根据函数项的次数分为线性和非线性微分方程。 ### 解决微分方程的定解条件 为了解决微分方程，除了方程本身外，还需要给出适当的定解条件，这包括初始值条件和边界值条件。初始值条件通常用于常微分方程，规定了解在某个特定点的值；而边界值条件则用于偏微分方程，规定了解在区域边界上的行为。这些条件对于唯一确定微分方程的解至关重要。 通过上述知识点的梳理，我们可以看到常微分方程数值解法在解决实际问题中的重要性和复杂性，以及各种数值方法的特点和适用范围。这为后续深入学习和研究提供了坚实的基础。