计算机辅助几何基础-了解回旋曲线

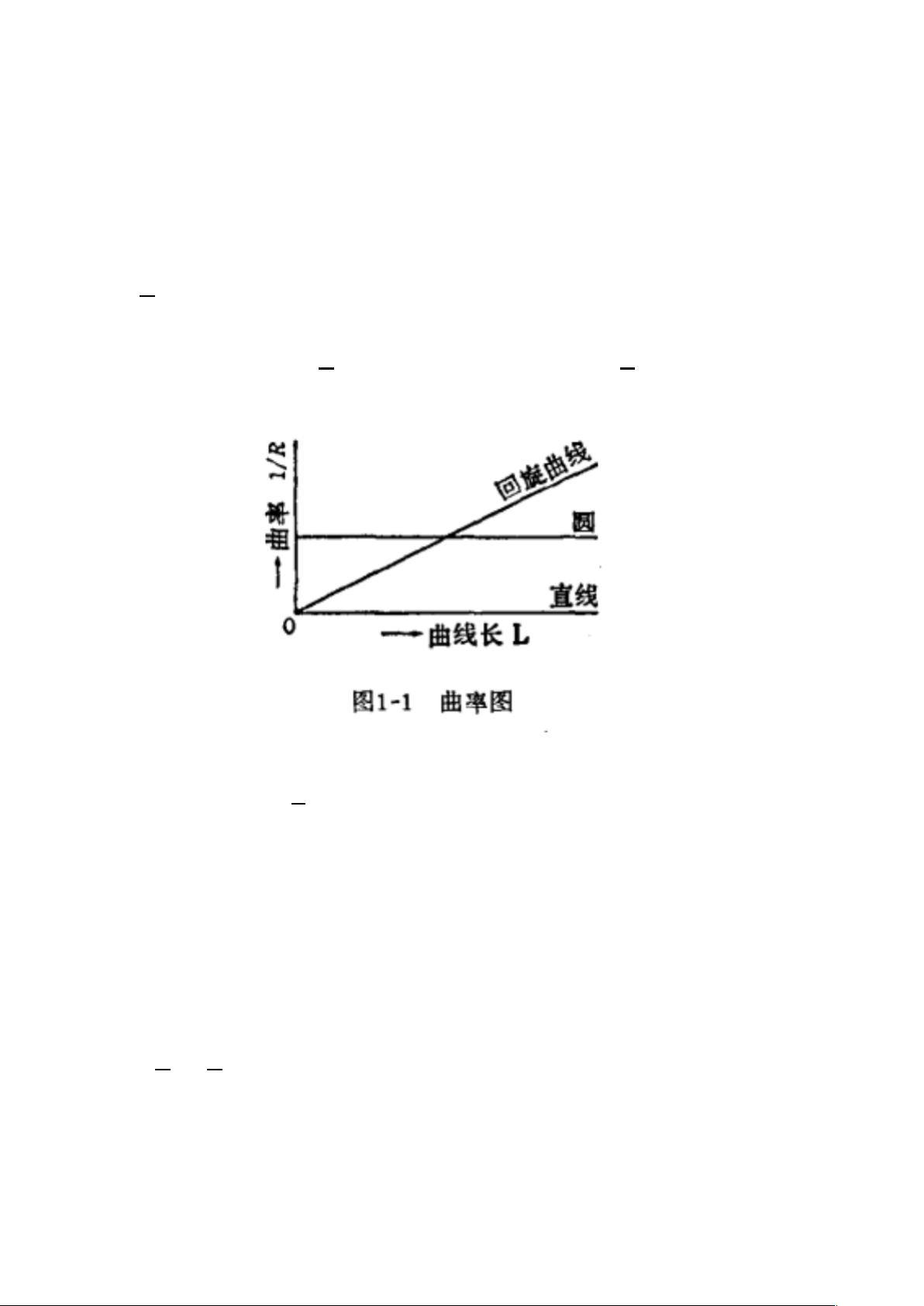
计算机辅助几何设计（CAGD，Computer-Aided Geometric Design）是现代工程和设计领域中的关键技术，它涉及如何使用计算工具来创建、分析和修改复杂的几何形状。在CAGD中，回旋曲线（Clothoid Curve）是一种重要的数学曲线，它在多种应用中起到关键作用，比如道路设计、动画制作、机械工程以及计算机图形学。 回旋曲线，又称为欧拉螺线或羊角螺线，是一种特殊的螺旋线。其特征在于曲线上任意一点的曲率与其到曲线起点的距离成正比，也就是说，曲率随着曲线长度线性变化。这种特性使得回旋曲线在需要平滑过渡的场合特别有用，因为它能够连续地调整弯曲程度，从而避免急剧的角变化。 公式1R = C × L 描述了这一关系，其中R代表曲线在某点的半径，L表示从曲线起点到该点的弧长，而C是一个常数。对于直线，其曲率是0（1R = 0），而对于圆，曲率是常数，即1R = C。通过改写这个公式，我们可以得到R × L = A^2，其中A是回旋曲线的一个重要参数，它衡量了曲线的大小。 如果我们将A设定为1，那么我们得到了单位回旋曲线，即R × L = 1。这意味着，对于所有具有相同参数A的回旋曲线，只要将单位曲线的几何特性乘以A，就可以得到相应尺度的回旋曲线。因此，所有的回旋曲线在几何上都是相似的，只是尺寸不同而已。 回旋曲线的性质如下： 1. 回旋曲线属于螺旋线的一类，但通常在实际应用中仅使用其靠近原点的部分，因为这里曲率变化更为平缓，适合实现平滑过渡。 2. 回旋曲线具有相似性。虽然它们都具有相同的形状，但通过改变参数A，可以生成无数不同大小的回旋曲线。 3. 参数A决定了曲线的曲率变化速率和曲线拐弯的急缓程度。A值越大，曲率变化越慢，曲线的拐弯就越平缓；反之，A值越小，曲率变化越快，曲线的拐弯就越急促。 在道路设计中，回旋曲线经常用于设计弯道，以确保车辆能安全且舒适地转弯。在其他领域，如动画和游戏设计中，回旋曲线可以用来模拟物体平滑的旋转运动。在机械工程中，它可以帮助设计出更加流畅的机械部件边缘，减少应力集中和磨损。 回旋曲线是计算机辅助几何设计中一个强大的工具，它的独特性质使其在各种工程和艺术设计中都有广泛的应用。理解和掌握回旋曲线的数学原理和特性，对于在这些领域进行高效工作至关重要。