曲线曲面基本理论.doc

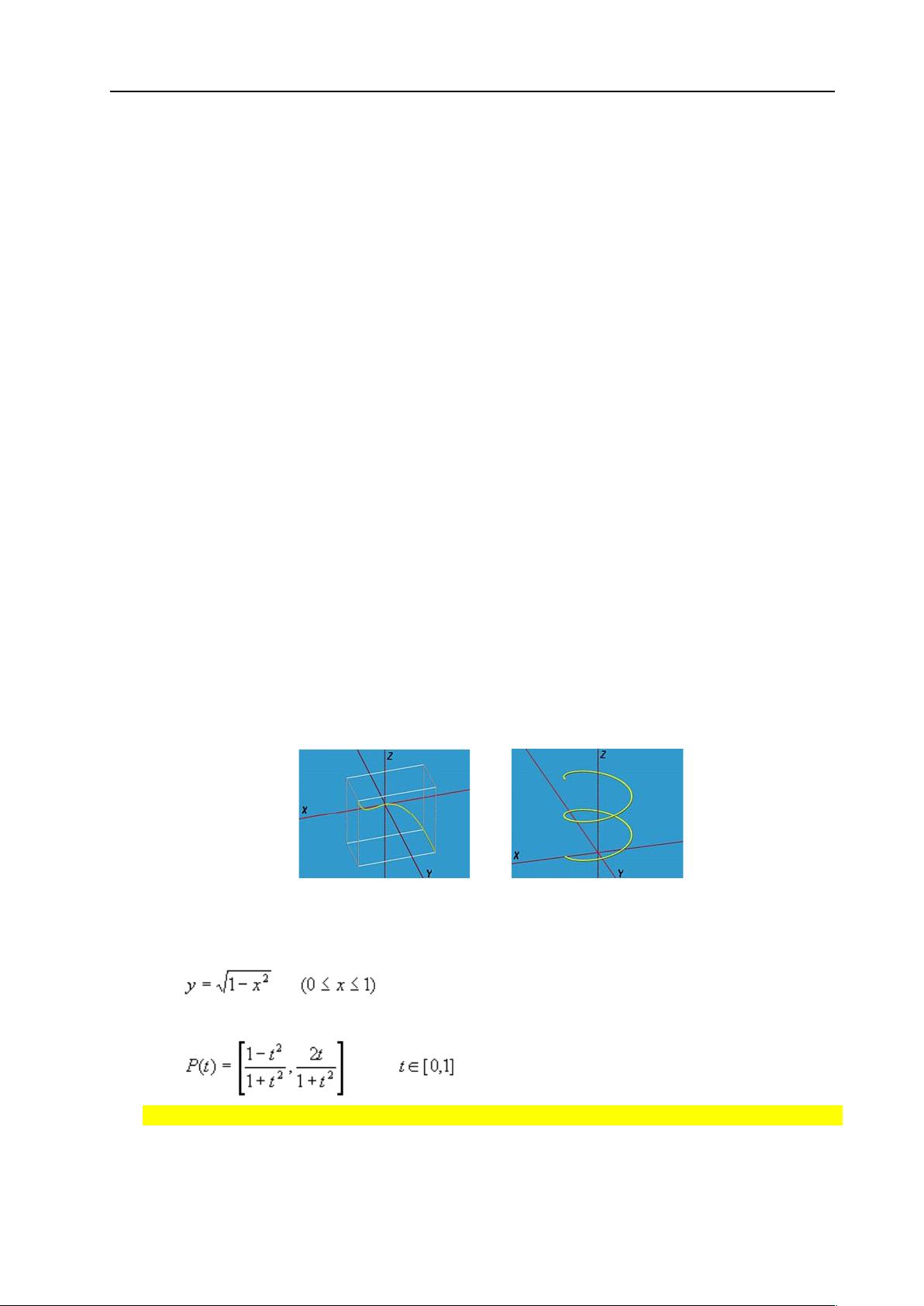
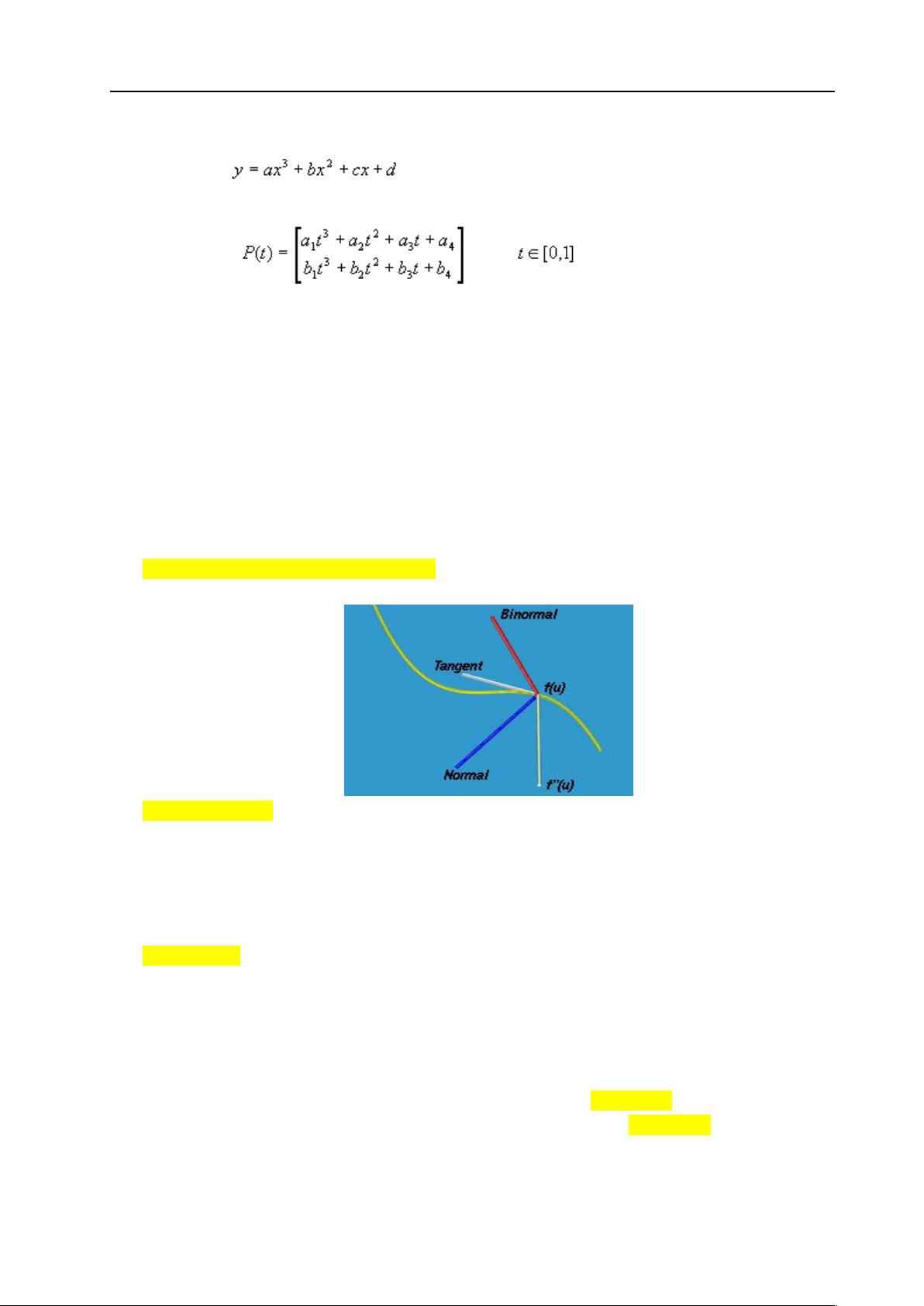
"曲线曲面基本理论" 曲面造型（Surface Modeling）是计算机辅助几何设计（Computer Aided Geometric Design，CAGD）和计算机图形学的一项重要内容，主要研究在计算机图象系统的环境下对曲面的表示、设计、显示和分析。曲面造型的发展历程可以追溯到二十世纪六十年代，Coons、Bezier 等大师奠定了其理论基础。经过三十多年的发展，曲面造型现在已形成了以有理 B 样条曲面（Rational B-spline Surface）参数化特征设计和隐式代数曲面（Implicit Algebraic Surface）表示这两类方法为主体，以插值（Interpolation）、逼近（Approximation）这二种手段为骨架的几何理论体系。 曲面造型的目的就在于解决复杂外形产品的表面问题，如飞机、汽车、轮船等。1963 年美国波音（Boeing）飞机公司的佛格森（Ferguson）最早引入参数三次曲线（三次 Hermite 插值曲线），将曲线曲面表示成参数矢量函数形式，构成了组合曲线和由四角点的位置矢量、两个方向的切矢定义的佛格森双三次曲面片，从此曲线曲面的参数化形式成为形状数学描述的标准形式。 1964 年，美国麻省理工学院（MIT）的孔斯（Coons）用四条边界曲线围成的封闭曲线来定义一张曲面，Ferguson 曲线曲面只是 Coons 曲线曲面的特例。而孔斯曲面的特点是插值，即构造出来的曲面满足给定的边界条件，例如经过给定边界，具有给定跨界导矢等等。但这种方法存在形状控制与连接问题。 1964 年，舍恩伯格（Schoenberg）提出了参数样条曲线、曲面的形式。1971 年，法国雷诺（Renault）汽车公司的贝塞尔（Bezier）发表了一种用控制多边形定义曲线和曲面的方法。这种方法不仅简单易用，而且漂亮地解决了整体形状控制问题，把曲线曲面的设计向前推进了一大步，为曲面造型的进一步发展奠定了坚实的基础。 但是，当构造复杂曲面时，Bezier 方法仍存在连接问题和局部修改问题。同期，法国雪铁龙（Citroen）汽车公司的德卡斯特里奥（de Castelijau）也独立地研究出与Bezier 类似的方法。1972 年，德布尔（de Boor）给出了 B 样条的标准计算方法。1974 年，美国通用汽车公司的戈登（Gorden）和里森费尔德（Riesenfeld）将 B 样条理论用于形状描述，提出了 B 样条曲线和曲面。这种方法继承了 Bezier 方法的一切优点，克服了 Bezier 方法存在的缺点，较成功地解决了局部控制问题，又轻而易举地在参数连续性基础上解决了连接问题，从而使自由型曲线曲面形状的描述问题得到较好解决。 但是，B 样条方法显示出明显不足，不能精确表示圆锥截线及初等解析曲面，这就造成了产品几何定义的不唯一，使曲线曲面没有统一的数学描述形式，容易造成生产管理混乱。1975 年，美国锡拉丘兹（Syracuse）大学的佛斯普里尔（Versprill）提出了有理 B 样条方法。80 年代后期皮格尔（Piegl）和蒂勒（Tiller）将有理 B 样条发展成非均匀有理 B 样条方法（即 NURBS），并已成为当前自由曲线和曲面描述的最广为流行的技术。 NURBS 方法的突出优点是：可以精确地表示二次规则曲线曲面，从而能用统一的数学形式表示规则曲面与自由曲面，而其它非有理方法无法做到这一点；具有可影响曲线曲面形状的权因子，使形状更宜于控制和实现；NURBS 方法是非有理 B 样条方法在四维空间的直接推广，多数非有理 B 样条曲线曲面的性质及其相应算法也适用于 NURBS 曲线曲面，便于继承和发展。由于 NURBS 方法的这些突出优点，国际标准化组织（ISO）于 1991 年颁布了关于工业产品数据交换的 STEP 国际标准，将 NURBS 方法作为定义工业产品几何形状的唯一数学描述方法，从而使 NURBS 方法成为曲面造型技术发展趋势中最重要的基础。 曲线、曲面的表示有三种形式：显式、隐式和参数表示。显式表示的曲线、曲面可以用 z ＝ f（x，y）表示，其中 z 是曲面高度，x、y 是水平坐标。隐式表示的曲线、曲面可以用 F（x，y，z）＝ 0 表示，其中 F 是一个函数，x、y、z 是曲面上的点。参数表示的曲线、曲面可以用矢量函数表示，例如 r（u）＝（x（u），y（u），z（u）），其中 u 是参数，x、y、z 是水平坐标。