算法设计期末考试题六_十章

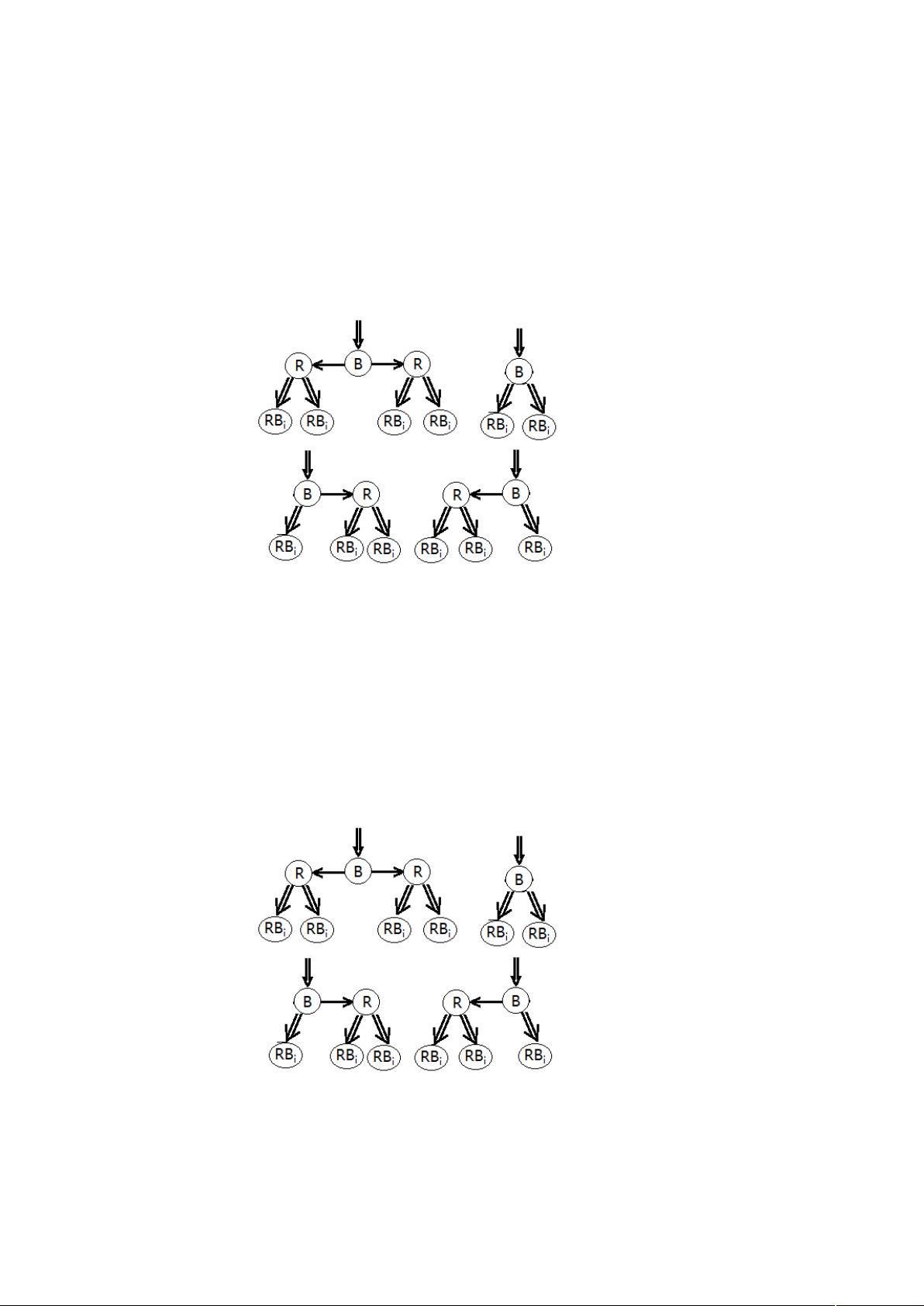
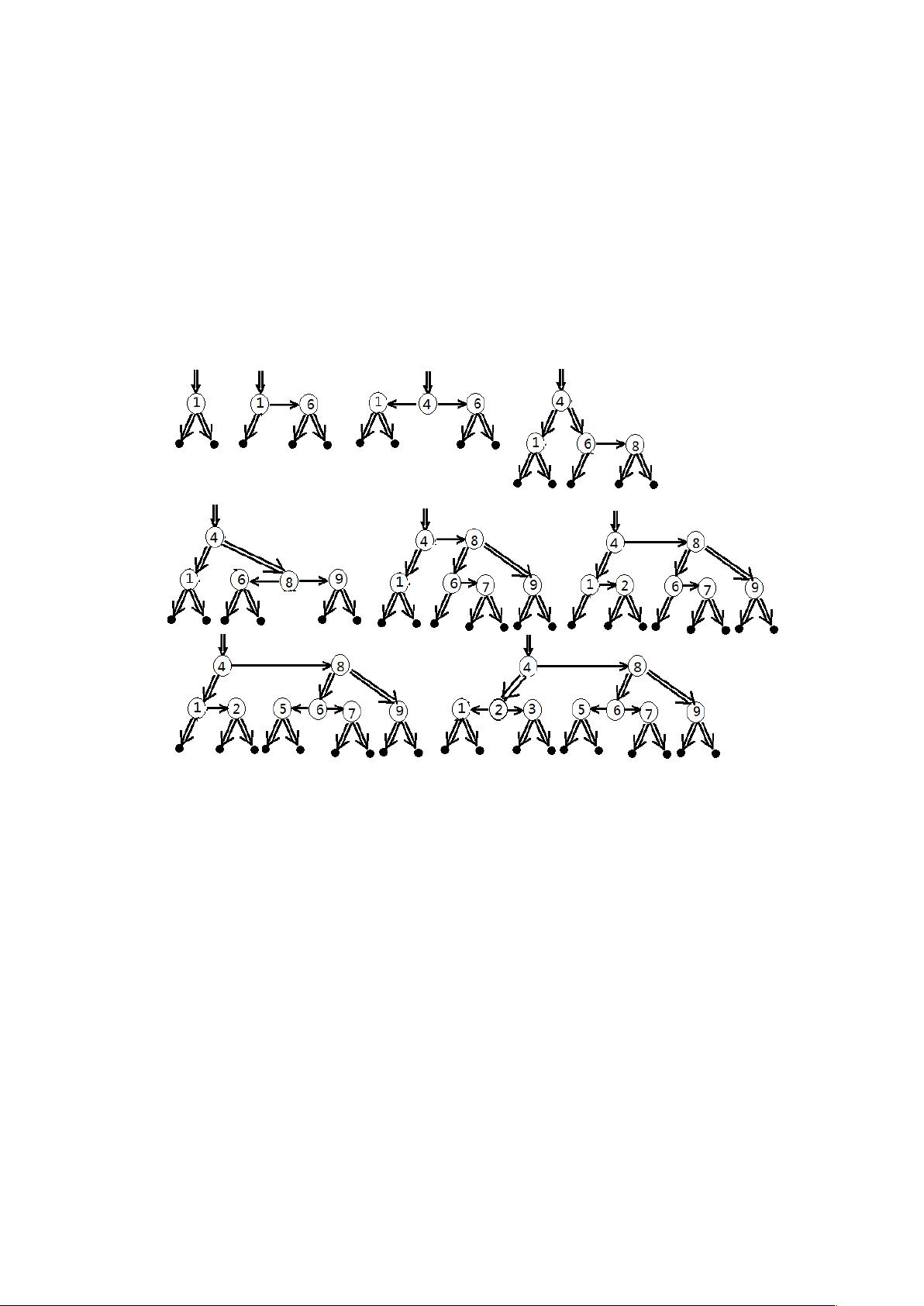
### 红黑树的关键属性与证明 #### 内部黑节点数的下限 **题目解析：** 给定的题目中要求证明一个黑色高度为\(h\)的红黑树，其内部黑节点数至少为\(2^{h}-1\)。 **证明：** 1. **基本情况**：当\(h=0\)时，红黑树只含有一个外部节点，此时的红黑树被称为\(RB_0\)，内部没有黑色节点，满足条件。 2. **归纳假设**：假设当红黑树的高度为\(i\)时，命题成立，即内部黑节点数\(N_i \geq 2^i-1\)。 3. **归纳步骤**：当红黑树的高度为\(i+1\)时，根节点的左右子树的高度分别为\(i\)或小于\(i\)。在最不利情况下，这两个子树都是高度为\(i\)的红黑树，根据归纳假设，每棵树至少有\(2^i-1\)个内部黑节点。因此，整棵树至少有\(2 \times (2^i-1)+1 = 2^{i+1}-1\)个内部黑节点，从而完成了证明。 #### 内部节点数的上限 **题目解析：** 需要证明黑色高度为\(h\)的红黑树，其内部节点数至多为\(4^{h}-1\)。 **证明：** 1. **基本情况**：当\(h=0\)时，红黑树为\(RB_0\)，即只有一个外部节点，内部没有节点，满足条件。 2. **归纳假设**：假设当红黑树的高度为\(i\)时，命题成立，即内部节点数\(M_i \leq 4^i-1\)。 3. **归纳步骤**：当红黑树的高度为\(i+1\)时，在最坏的情况下，根节点的左右子树都是高度为\(i+1\)的红黑树，但因为红黑树的性质限制了红色节点的存在方式，实际上这种情况不会发生。最坏的情况是左右子树均为高度\(i\)的最大节点数红黑树。根据归纳假设，每棵树最多有\(4^i-1\)个内部节点，加上根节点自身，整棵树最多有\(2 \times (4^i-1) + 1 = 4^{i+1}-1\)个内部节点，完成证明。 #### 黑色节点深度的限制 **题目解析：** 要证明任意黑色节点的深度最多是其黑色深度的2倍。 **证明：** 在红黑树中，任何路径上都不会出现连续的红色节点。设黑色节点的深度为\(h\)，即从根到该节点的路径长度。设路径上的红色节点数为\(x\)，黑色节点数为\(y\)，则有\(x \leq y\)。因此，路径长度\(h = x + y \leq 2y\)，表明任何黑色节点的深度不超过其黑色深度的两倍。 ### 数组动态扩容策略对比 在数组需要扩大时，有两种策略：将当前数组大小乘以4或乘以2。在时间和空间效率方面： - **乘以2的策略**：每次扩容，总耗时为\(T = t*(n+n/2+n/4+…+n/2^{k-1}) \leq 2nt\)。 - **乘以4的策略**：每次扩容，总耗时为\(T = t*(n+n/4+n/16+…+n/4^{k-1}) \leq 4nt/3\)。 **空间消耗**：乘以2策略分配两倍空间，而乘以4策略分配四倍空间。 ### 最长非降子序列问题 对于给定序列，要找到其中的最长非降子序列。解决这个问题的算法通常使用动态规划： - 定义数组`maxLength[n]`和`preEle[n]`，其中`maxLength[i]`存储到第\(i\)个元素为止的最长非降子序列的长度，`preEle[i]`存储该子序列中第\(i\)个元素前一个元素的索引。 - 初始时，`maxLength[1] = 1`，`preEle`数组全为0。 - 对于每个元素，通过比较其与前面所有元素的大小，更新`maxLength[i]`和`preEle[i]`。 - 时间复杂度为\(O(n^2)\)，其中\(n\)为序列长度。 ### 二叉树的种类 对于具有\(n\)个节点的二叉树，计算可能的不同结构数量是一个经典的组合数学问题，具体公式涉及卡特兰数(Catalan Number)，其表达式为： \[C_n = \frac{1}{n+1} {2n \choose n}\] ### 矩阵链乘法的优化 对于矩阵链乘法\(A_1 \times A_2 \times \ldots \times A_n\)，要找到最优的乘法顺序以最小化操作次数，可以使用动态规划解决。关键在于构建一个二维数组，记录不同矩阵段之间相乘的最小成本，并利用该数组来确定最佳乘法顺序。这种方法同样具有\(O(n^3)\)的时间复杂度，但在实际应用中能显著减少不必要的矩阵乘法操作，从而提高效率。