没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

1
姜萍那道题的几何证明
kipo 2024
年
7
月
30
日
各位看官好,在下
kipo
。
姜萍做的那道题我也做了,用的是比较直观的几何解法。
这就是姜萍做的那道题(网传阿里要求的,后来辟谣了)
姜萍的解法用到了
Γ
函数。
Γ
函数就是伽马函数,
Γ
音
Gama
,大写希腊字母,大家比较熟
悉的是它的小写形式
γ
,经常用来表示一种射线(这是照顾下我朋友圈里的朋友,各个年近
半百,多年不学数学了)。这函数在同济第七版高数第
268
页,与积分相关,再具体一点就
是余元公式,大家记不起来的可以翻翻课本。我上学时学的经济类的数学,同济版的是毕业
后自学的。
那
Γ
函数太抽象,然后还要求导,我看了直接蒙圈。关键是即使用这种方法把题证明了,
我们似乎感受不到背后发生了什么。尤其像我这种脑子比较笨的,如果数学表达不能联系到
一些物理量或者几何图形,感觉就是似懂非懂,其实就是完全没懂,但是如果能映射到物理
或者几何,最好再拍成动画片,那就非常适合我了。
闲言少叙,我来讲讲我的解题历程。原题需要做一些基本的变换。
1.
题出的有误,
ω
定义域的限定的不全,
ω
不能等于
-2πk
,这是显而易见的。
2.
左式:把分母中
π
提到括号外面变成
π
2
括号里面就变成了
(k+ω/2π)
。
(csc
是余割函数,与正弦互为倒数,
sinα·cscα=1
,照顾下我朋友圈里的老人,见谅
)
3.
因为左式是从
k=- ∞
一直加和到
k=+∞,
如果
ω/2π
的整数部分是
N
,小数部分是
x
,
然后我们把括号里
ω/2π
换成
x
的话,求和时
k
的上下界需要加
N
,以保持与原式等价,但是
±∞+N=±∞,
没变化,所以
ω/2π
可以直接替换成其小数部分
x
。
我们令
x=ω/2π
的小数部分,这样一来表达式变简单了很多,这主要的是为了我本次打
字排版方便。这种事在下也是第一次干。
x
∈
(-1,1)
但是
x≠0.
4.
这样一来,原式左边(我们把它设为
S
)就变成了下面的
S1 + S2,
由于对应函数的
对称性,我们只研究
x
∈
(0,1)
便可。
S=S1+S2
S1= ( )/π
2
S2= ( )/π
2
显而易见:
S2 =( )/π
2
这一下子让我想到了巴塞尔问题,也就是所有自然数平方后取倒数加和,从分类上讲,
这个属于黎曼
ζ
函数
ζ(s)
。嗯,黎曼函数,研究过的都知道,这个非常的高大上。我忽然想起
电影《功夫》里的一句台词:
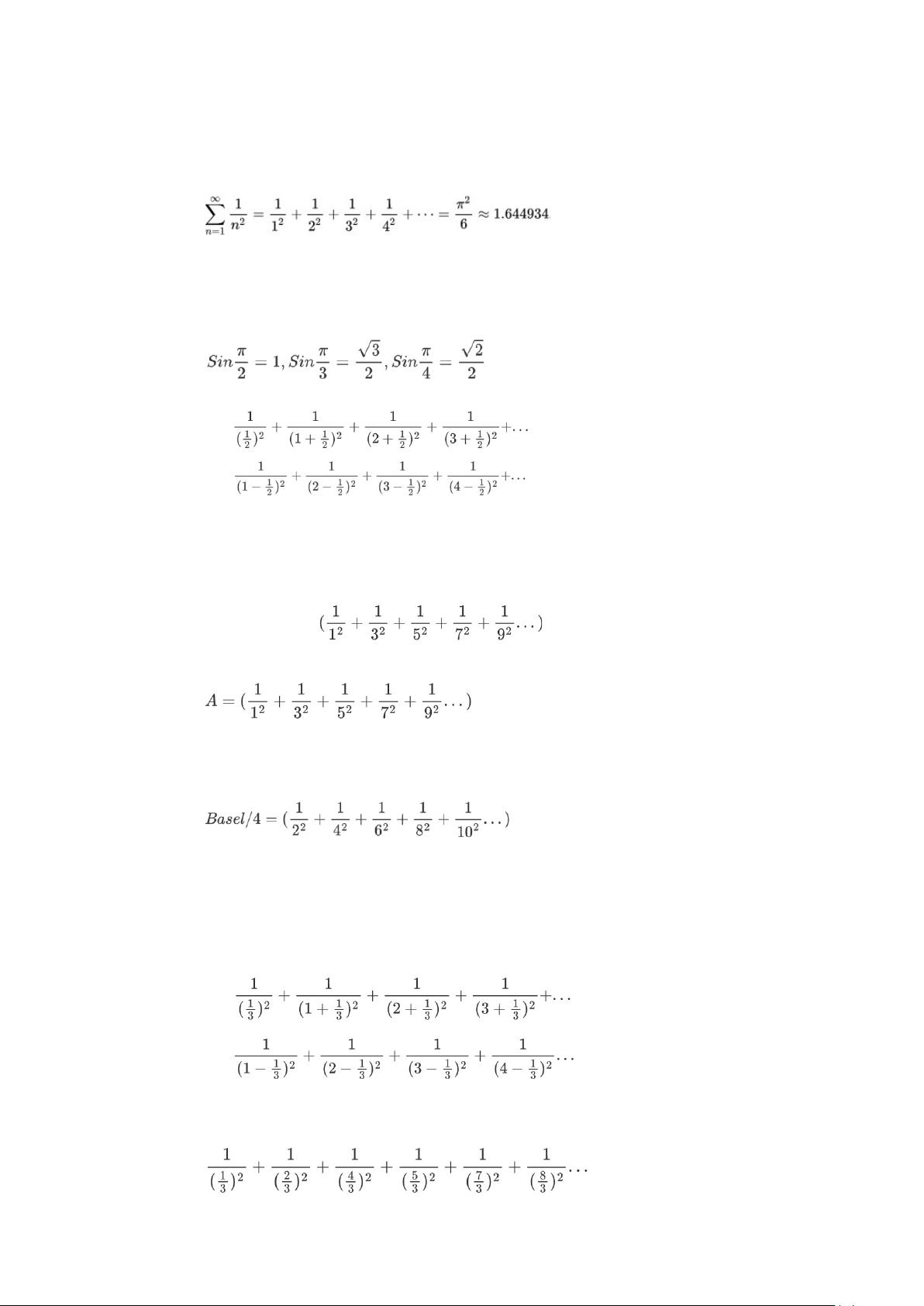
2
“
难道我研究过黎曼猜想,也要说给你听吗?
”
巴塞尔问题是大神欧拉解出来的,结果是
π
2
/6
(如下)。解法用到了正弦函数的级数表
达式。当然由于本人喜欢看动画片,所以我能记住的自然是
3Blue1Brown
的几何解法动画片。
我们用
Basel
(巴塞尔)表示这个和。那么能不能利用巴塞尔问题的结论,来求解
原题呢?我们先试几个特殊值:
x=1/2, 1/3, 1/4
时,
Sinπx
:
x=1/2
时,左边
S = S1+S2
S1=( )/π
2
S2=( )/π
2
分母平方之前
, S1
:
0.5,1.5,2.5,3.5.....
然后
S2
再来一遍:
0.5,1.5,2.5,3.5.....
如果把所有分母放大到原来的
4
倍(平方前放大到原来
2
倍),分母变大分时分式值变
小。
S
变为
S/4
。
分母
x2(
平方之前
)
变为:
S1
:
1,3,5,7,9,...
然后
S2
再来一遍,
2
倍。
所以
S =S1+S2=(4+4) /π
2
我们设
A
其实等于
π
2
/8
,这是一个现成的结论。当然也可以用巴塞尔数列和为
π
2
/6
来求。方法
还是放缩法,巴塞尔数列的每一项分母放大为原来的
4
倍(变为偶数平方倒数和),其值为
原值的
1/4
:
如此所有奇数倒数的平方和就等于
Basel
值的
3/4 (Basel
级数排除偶数项,剩余奇数项
)
。
因此
A=π
2
/6*(3/4)=π
2
/8.
于是
S=8A/π
2
=1.
而
x=1/2
时,
Sin
2
πx=1,csc
2
πx=1,
右边也等于
1
。所
以我们证明了
x=1/2
时,原式成立。
X=1/3
时,左边
S = S1+S2
S1=( )/π
2
S2=( )/π
2
S=S1+S2
:
3
把分母放大为原来的
9
倍:
然后上下加在一起
=Basel
数列里扣除了分母为
3 6 9...
各项,而这些项是
Basel
值的
1/9
(
Basel
级数各自然数平方之前先
X3
,平方后
Basel
值为原值
1/9
),则留下来的项是
Basel
的
8/9
。所以
π
2
S=π
2
(S1+S2) = (π
2
/6)*(8/9)*9=4π
2
/3.
所以
S=4/3.
因此
x=1/3
时
Sin
2
πx=Sin
2
(π/3)=3/4, csc
2
(π/3)=4/3.
原式成立。
同样的方法可证
x=1/4
时原式成立,我现在感觉很累,主要是
LaTex
不熟练,老出错,
所以
x=1/4
的证明我就省略了。(
x=1/4
时
S=2
)顺便说一句,我之前都从没听说过
LaTex
,
这次为了写这个题的解法,我现学的。所以有人这个用来质疑姜萍似乎不妥。
好了,我们可以观察到
1
)在两个定义域内,左式
S
是个连续变化的函数,且可导。
2
)在
(0,1)
区间内,我们找到了三个值让等式成立,
1/2
,
1/3
,
1/4
。(当然在
(-1,0)
这
个定义域,当
x
的值为
-1/2
,
-1/3
,
-1/4
时等式也成立)
这确实令人鼓舞,但是很遗憾,其他的值很难用类似的方法求出来,而且其他的值也无
法用这些已经求出的值进行线性表达,这确实让人很沮丧。当然以上至少可以证明原题应该
没有出错,而我们没有浪费力气。嗯,这句话显然不是一种数学证明。
所以,为了证明等式成立,我们得换一种方法。我用的是
3Blue1Brown
关于巴塞尔问题
一模一样的方法,也就是灯塔模型。其实我本来想用万有引力模型,因为在下喜欢物理,而
万有引力也和距离的平方成反比,但是万有引力是个矢量,加和时会引起麻烦,所以还是用
灯塔模型吧。所谓灯塔模型,就是一个人接收到灯塔的光的强度和这个人离灯塔的距离的平
方成反比,可以贴合原题。然后呢,故事背景是这样的:
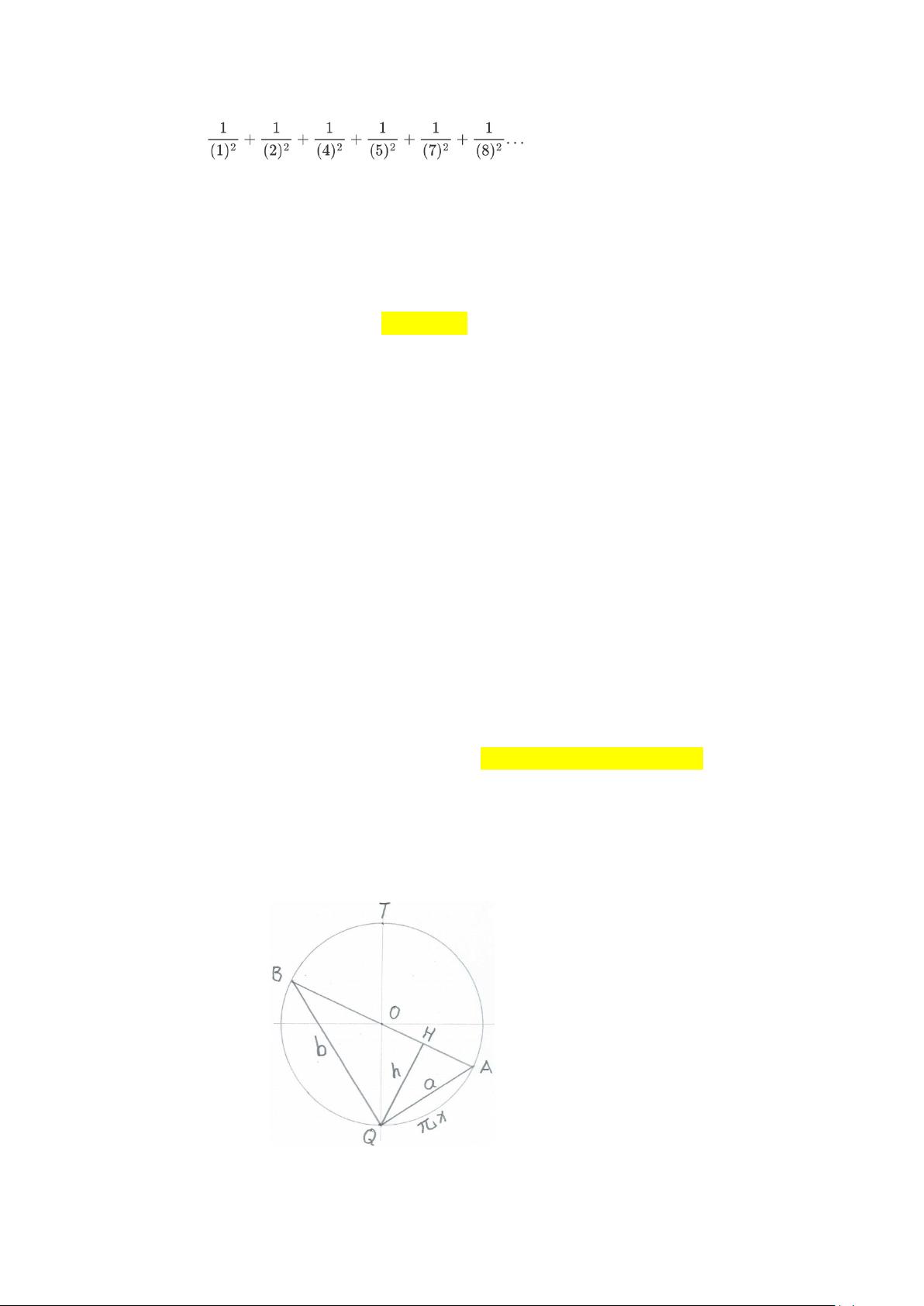
有一个圆形的湖面(也就是一个单位圆),周长为
2π
,半径
r=1
,直径
d=2
。圆上有两
点
A
、
B
(两个灯塔),注意,以后还会有更多灯塔,但是不管有多少灯塔,每个灯塔的亮
度都一样。两灯塔
AB
连线过圆心
O
,所以
AB
为直径
,
其长度为
d=2
。观察者
Q
在底部
6
点
钟位置(在下姓祁,就是那个
Q
,因为
k
已经用了,所以只能用
Q
),
QA=a
,
QB=b
,
H
位
于
AB
上,
QH
垂直于
AB
。
QH=h
(△
QAB
的高)。
T
在顶部(
Top
)
12
点位置,弧
QA
长为
πx
。
于是:
剩余10页未读,继续阅读
资源评论

kipo320
- 粉丝: 0
- 资源: 2
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 精选微信小程序源码:汤总便利小程序(门店店铺类)小程序(含源码+源码导入视频教程&文档教程,亲测可用)
- Excel弹窗“此工作簿包含到一个或多个可能不安全的外部源的链接” 场景范例
- C语言《基于ROS melodic,底盘控制器基于STM32的一个2D激光SLAM自主导小车》+项目源码+文档说明
- winform上位机图像采集控件.zip
- 工具变量全国供应链创新试点城市DID数据集(2007-2023年).xlsx
- SasAppsUserKeyBarUserTech_86_1.0.0.1.kop
- 项目售后服务及培训.docx
- 贪心算法介绍及入门案例
- 项目实施管理方案.docx
- 精选微信小程序源码:熊猫签证小程序(含源码+源码导入视频教程&文档教程,亲测可用)
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功