2013届高考选修4-4坐标系与参数方程第2讲参数方程.ppt

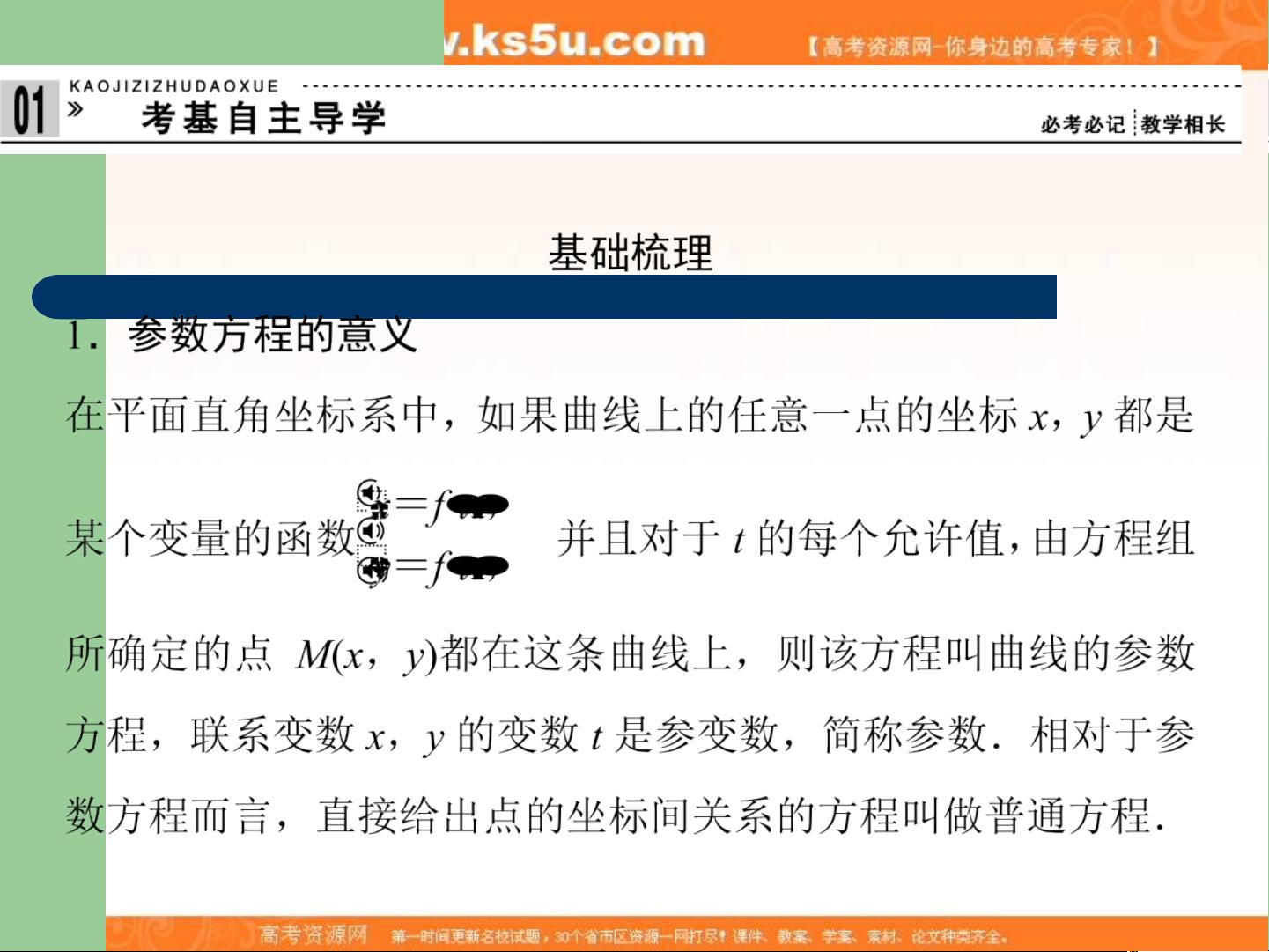
在高中数学的学习中，坐标系与参数方程是解析几何中的一个重要部分，特别是在解决曲线问题时，参数方程显得尤为实用。2013届高考选修4-4的这一讲主要聚焦于如何理解和运用参数方程来描述复杂的几何轨迹。下面我们将详细探讨参数方程的概念、特点以及在实际问题中的应用。 一、参数方程的定义 参数方程是一种用来表示平面上或空间中曲线的方法，它将曲线上的每一点与一组特定的变量（称为参数）关联起来。一般形式为： \[ x = f(t) \] \[ y = g(t) \] 其中，\( t \) 是参数，\( f(t) \) 和 \( g(t) \) 是关于 \( t \) 的函数，它们共同决定了点 \( (x, y) \) 在曲线上的位置。参数 \( t \) 的取值范围决定了曲线的完整形状。 二、参数方程的特点 1. 灵活性：参数方程可以描述任何形状的曲线，包括直线、圆、抛物线等，甚至是一些非代数曲线。 2. 可以反映运动轨迹：参数方程特别适合描述物体在时间和空间中的运动轨迹，因为 \( t \) 可以视为时间变量。 3. 参数化：通过参数方程，可以将多元方程组简化为一元方程，方便求解和分析。 三、参数方程的转换 1. 消元法：如果参数方程组是线性的，可以通过消元法将参数 \( t \) 消去，得到直角坐标系下的普通方程。 2. 参数积分：对于某些情况，可以通过对参数 \( t \) 进行积分，找出曲线的长度或者面积等几何性质。 四、参数方程的应用 1. 物理学：在物理学中，参数方程常用于描述物体的运动轨迹，如抛体运动、圆周运动等。 2. 工程学：在工程计算中，如计算机图形学，参数方程用于生成复杂的曲线和曲面，如贝塞尔曲线和NURBS（非均匀有理B样条）。 3. 统计学：在统计建模中，参数方程可以用来描述数据的分布和趋势。 五、实例分析 在高考中，可能会遇到利用参数方程求解曲线的切线、弧长、极坐标转换等问题。例如，已知一个参数方程 \( x = t^2 \)，\( y = t^3 \)，要求解在 \( t = 1 \) 处的切线斜率。此时，可以通过对 \( x \) 关于 \( t \) 求导得到切线斜率，即 \( \frac{dx}{dt} \) 在 \( t = 1 \) 时的值。 总结来说，参数方程是解析几何中一种强大的工具，它能帮助我们更直观地理解并处理复杂的几何问题。在高考复习中，熟练掌握参数方程的运用不仅有助于提高解题效率，也能提升对几何概念的深入理解。