reconstructed without a priori knowledge of the image content [15].
To achieve reconstruction may be computationally expensive
[28,29], whilst simpler techniques, such as an image interpolation,
are usually not adequate to support subsequent reliable image
processing. Hence, it is important to consider the development of
algorithms that can be applied directly on irregularly sampled
images as well as regular complete data. In this context, we present
details of the design of gradient operators that can naturally alter
their shape in accordance with the local data distribution, enabling
them to be applied directly both to irregularly distributed range data
without any pre-processing requirements and to regularly distrib-
uted intensity data. Where multi-scale or scale adaptive edge
extraction is to be implemented, the design procedure facilitates
multiple operators to be developed over a range of scales.
Finite element methods have been introduced into a number of
areas of image processing, for example medical image processing
[8,22,26], analysis of human joints [7], model ling geomaterials [31],
and surface restoration [10]. Less research has been undertaken using
finite element methods for the development of low level neighbour-
hood operators. However, recent work in this area includes the
systematic development of families of low-level image processing
operators, using finite element based image derivative approximati on
such as those in [11,24].In[25], we presented a brief overview of multi-
scale gradient operators for direct use on range images designed within
the finite element framework. In this paper, we extend the work in [25]
by showing the details of the gradient operator design and imple-
mentation, providing detailed evaluation of the approaches, and
demonstrating how the flexibility of this approach enables us to apply
the multi-scale technique to either range or intensity images without
any modification to the operator design or any costly image pre-
processing. Section 2 provides a detailed overview of the multi-scale
algorithm, with Section 3 providing details of how features are
determined in range images using gradient operators. Section 4
provides evaluation results, demonstrating the accuracy of our
approach on both range and in tensity image data. A summary and
details of the future work are provided in Section 5.
2. Irregular directional derivative operators
The directional derivative of the image is one of the fundamental
building blocks in image processing. Image processing operators
are often based on first derivative approximations, for which it is
necessary that the image obtained from the acquisition device is
modelled by a function, say u(x, y), that is constrained to belong to
Hilbert space H
1
ð
O
Þ over the image domain
O
; i.e. the integral
R
O
ð9u9
2
þu
2
Þd
l
is finite, where u is the vector ð@u=@x, @u=@yÞ
T
and
l
is
Lebesgue measure on
O
. In this section, we describe how the shape
adaptive directional derivative operator design procedure is based
on an approximation, Uðx, yÞ, of the image function uðx, yÞ.
2.1. Image data representation
To design operators that can be applied to both regularly
distributed intensity image data and irregularly distributed range
image data, we initially consider the more complex image repre-
sentation. Therefore, we represent the image as a grid of irregularly
distributed samples of a continuous function U(x, y) on a domain
O
.
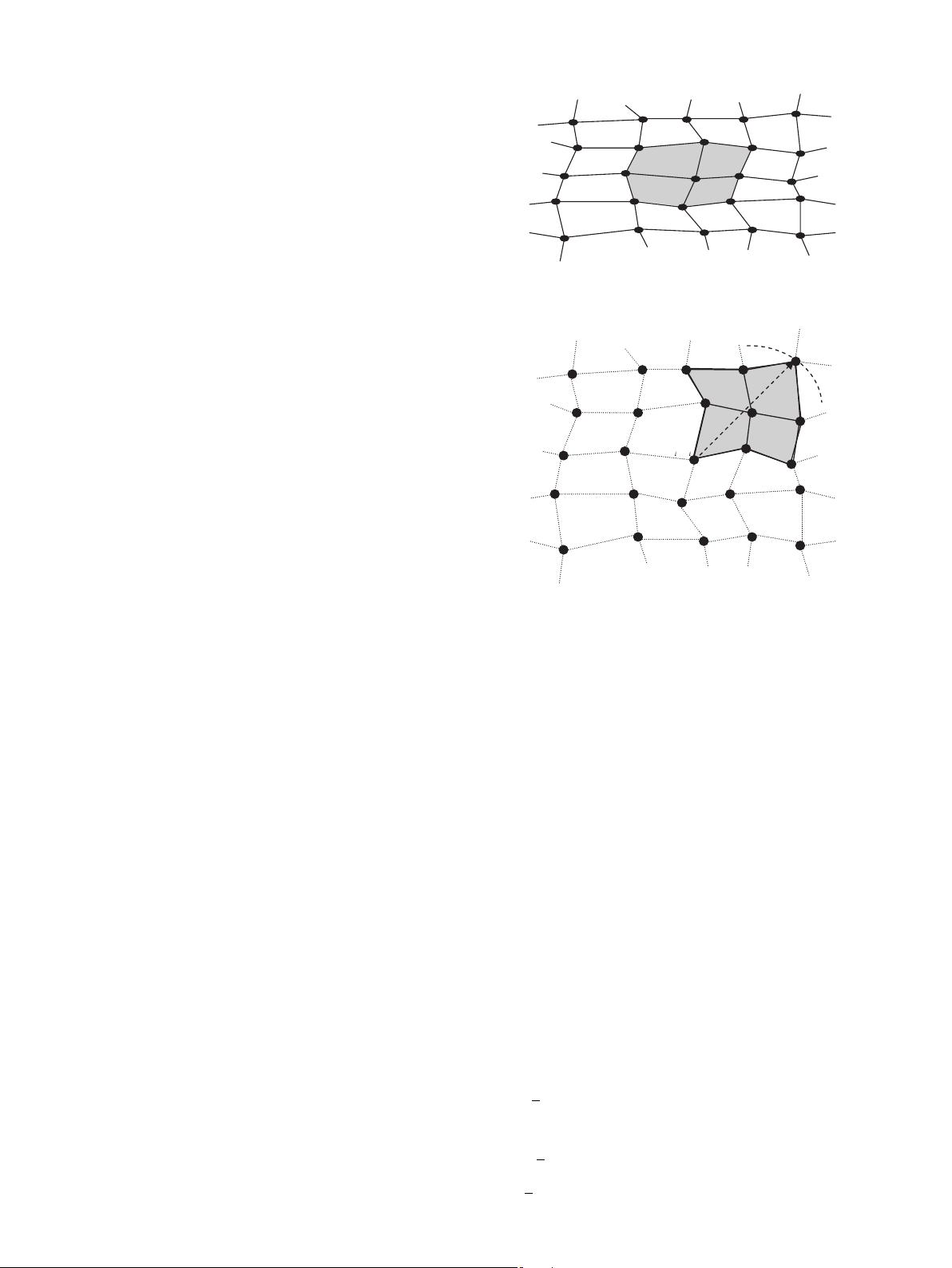
A quadrilateral mesh is then applied to the irregular image
representation and the nodes are pixel values, as illustrated in
Fig. 1. Each node (x
i
, y
i
) in the quadrilateral mesh has an associated
piecewise bilinear basis function
f
i
(x, y) which has the properties
f
i
ðx
j
, y
j
Þ¼
1ifi ¼ j
0ifia j
:
(
ð1Þ
Thus,
f
i
(x, y) is a ‘‘tent-shaped’’ function with support restricted to a
small neighbourhood centred on node (x
i
, y
i
) consisting of only those
elements that have node (x
i
, y
i
) as a vertex (shown as the shaded region
in Fig. 1). We then approximat ely represent the image by a function
Uðx, yÞ¼
X
N
j ¼ 1
U
j
f
j
ðx, yÞð2Þ
in which the parameters fU
1
, ..., U
N
gare the image pixel values at the N
irregularly located nodal points in the mesh. Therefore, an approximate
image representation takes the form of a simple function on each
element and has the sampled range value U
j
at node (x
i
, y
i
).
2.2. Shape adaptive operator design
We describe the finite element framework adopted for the
development of the multi-scale directional derivative operators
using the 5 5 irregular operator illustrated in Fig. 2 as an example.
Similar to [11,24,25], we develop image processing operators that
correspond to weak forms in the finite element method [5].
Operators used for smoothing may be based simply on a weak
form, for which it is assumed that the image function u(x, y) belongs
to Hilbert space H
0
ð
O
Þ; i.e. the integral
R
O
u
2
d
l
is finite. Image
processing operators based on first derivative approximations
require the image function uðx, yÞ to belong to Hilbert space
H
1
ð
O
Þ. Corresponding to a directional derivative
@u=@b
b u ð3Þ
we may use a test function vA H
1
ð
O
Þ to define the weak form
EðuÞ¼
Z
O
b uvd
l
ð4Þ
where
b ¼ðcos
y
, sin
y
Þ is the unit direction vector.
),(
ii
yx
Fig. 1. Sample of the irregularly distributed image, showing a neighbourhood
around the node with co-ordinates ðx
i
, y
i
Þ.
1
ρ
i
w
),( yx
Fig. 2. Local 5 5 operator neighbourhood around the node with co-ordinates
ðx
i
, y
i
Þ, showing quadrant 1 (shaded) with radius w
1
i
r
.
S.A. Coleman et al. / Pattern Recognition 44 (2011) 821–838822



 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功