金融投资组合优化中基于一致模糊环境的多期选择模型研究及其应用资源-CSDN文库

版权申诉

148 浏览量 2025-01-06 20:48:38 上传评论收藏 1.47MB PDF 举报

资源推荐

资源详情

资源评论

Applied Soft Computing 114 (2022) 108104

Contents lists available at ScienceDirect

Applied Soft Computing

journal homepage: www.elsevier.com/locate/asoc

Multi-period portfolio selection under the coherent fuzzy

environment with dynamic risk-tolerance and expected-return levels

Xiaomin Gong

a,b

, Liangyu Min

c,d,

∗

, Changrui Yu

Institute of Fintech, Shanghai University of Finance and Economics, Shanghai 200433, China

School of Finance, Shanghai University of Finance and Economics, Shanghai 200433, China

Faculty of Business Information, Shanghai Business School, 201400, China

School of Information Management and Engineering, Shanghai University of Finance and Economics, Shanghai 200433, China

a r t i c l e i n f o

Article history:

Received 13 January 2021

Received in revised form 12 September 2021

Accepted 20 October 2021

Available online 25 November 2021

Keywords:

Multi-period portfolio selection

Coherent fuzzy numbers

Heterogeneity

Dynamic risk-tolerance/expected-return

level

a b s t r a c t

We discuss the portfolio selection problems in which the uncertainty of future returns and the

heterogeneity of investor attitudes towards the stock market (optimistic–pessimistic–neutral) are

captured by coherent fuzzy numbers. Two coherent fuzzy multi-period portfolio selection models

are developed from the perspectives of wealth maximization and risk minimization. Given that the

constraint levels regarding risk and return of the current period tend to be influenced by the outcome

of the previous period, the dynamic risk-tolerance and expected-return levels are integrated into

the portfolio modeling. Practical constraints and transaction costs are also taken into account, which

enables the models more effective and lifelike in simulating the real-world trading of the stock market.

The empirical studies based on two large data sets are presented to illustrate the applicability of

the proposed models. To survey the models’ performance, several portfolio evaluation criteria are

used to conduct out-of-sample analysis. The results show outstanding performance of the presented

models with dynamic strategies over conventional ways (static risk-tolerance and expected-return

levels) on most of the indicators. This research offers references for investors with different attitudes to

make long-term investment decisions, and is an effective supplement to behavioral portfolio selection

research based on bounded rationality under uncertainty.

1. Introduction

Constructing the optimal portfolios by the selection of proper

financial assets is among the most vital and concerned decision-

making problems in the realm of financial management and

financial engineering, and it is also a basic mission for individual

and institutional investors. The pioneering work of Markowitz [1],

generally known as the mean–variance model, offers a brand

new perspective for the research of portfolio selection and lays

the foundation of modern portfolio theory. Mean–variance model

describes portfolio selection as a bi-objective optimization prob-

lem, with the aim of delivering an appropriate trade-off be-

tween portfolio return and risk [2–4]. In the model, portfolio

return is defined as the weighted linear combination of returns

of constituent assets, and portfolio risk is quantified by portfolio

variance, namely the function of correlations in assets compo-

nents [5]. Based on Markowitz’s framework, the literature has

seen a proliferation of several extended portfolio selection models

∗

Corresponding author.

E-mail addresses: gongxiaomin961@163.com (X. Gong),

minux@163.sufe.edu.cn (L. Min), yu.changrui@mail.shufe.edu.cn (C. Yu).

that are more aligned with the real-world portfolio management

requirements by considering the complex realistic constraints

and criteria [6–12].

Significantly, the traditional portfolio optimization models fo-

cus solely on a single period, that is, only the one-shot decision

is provided from the beginning to the end of the investment

period. However, such strategies cannot satisfy practical con-

cerns well since the real stock market is diverse and imperfect,

and investors will adjust their portfolio structure flexibly in re-

sponse to the dynamic and changeful market environment. It

is necessary to cast off the traditional modeling path and shift

the focus of the portfolio selection studies to multiple periods

to provide the best investment decisions for different periods.

Solving the multi-period portfolio problems also has a signifi-

cant history of research [13]. In particular, based on the mean–

variance framework, Çelikyurt and Özekici [14] presented some

mathematical optimization models under stochastic markets for

multi-period investment decisions. Fu et al. [15] explored the

mean–variance portfolio selection problem under continuous-

time conditions considering the constraint of higher borrow-

ing rates. Rocha and Kuhn [16] proposed a multistage model

in the mean–variance framework for portfolio management of

https://doi.org/10.1016/j.asoc.2021.108104

X. Gong, L. Min and C. Yu Applied Soft Computing 114 (2022) 108104

the power market. Wu and Li [17] established a multi-period

portfolio selection model in the mean–variance framework with

regime-switching, which assumes that cash flows are random.

Fu et al. [18] studied the optimal asset allocation issue under

the continuous-time regime-switching market. Cui et al. [19]

developed the time-consistent and self-coordination strategies

to address the time inconsistency of the multi-period mean-

Conditional Value-at-Risk portfolio selection problem.

However, the above-cited works on multi-period asset alloca-

tion are based on the assumption that future return information

associated with various assets could be exactly reflected through

past performance (data) and characterized by random variables.

In fact, financial markets involve high uncertainty, and there are

various factors that deviate from probabilistic analysis, such as

social, economic, political, investor’s psychology, and data uncer-

tainty, which usually affect the market and cannot be resolved

with probability theory [20–22]. Concerned with this issue, an

increasing number of scholars turn their attention to the fuzzy set

theory [23], which is referred to as an appropriate and powerful

means for processing uncertainty and vagueness that are the

inherent nature of any financial market [24]. Research on single-

period/multi-period portfolio decision and optimization in the

context of fuzzy logic is enriching and extending gradually. For in-

stance, Mehlawat et al. [25] developed a multi-objective portfolio

selection model integrating higher moments and efficiency. The

asset data in their work are modeled with (λ, ρ) interval-valued

fuzzy numbers to reflect the nondeterminacy as well as fuzziness

of the real-life stock market. Mansour et al. [26] presented a

financial portfolio selection method considering return, risk, and

liquidity criteria, which determines the possibility distributions of

fuzzy return according to the information provided by the deci-

sion environment. Liu et al. [27] studied the issue of fuzzy multi-

period portfolio selection that involves various aspects, such as

return, transaction cost, risk, and skewness. Liu and Zhang [28]

examined what time-varying loss aversion does to fuzzy multi-

period portfolio decision. Borovička [29] proposed a complicated

and rational procedure for portfolio formulation by utilizing the

fuzzy multiobjective programming technique with a unique in-

teractive program. Taking stock returns as fuzzy variables, Guo

et al. [30] formulated the fuzzy multi-period portfolio selection

approach in the view of different investment horizons. Liagk-

ouras and Metaxiotis [31] examined the multi-period portfolio

optimization problem involving transaction costs, in which the

asset-related information in every investment period is expressed

as trapezoidal fuzzy variables.

In real financial markets, investors exhibit substantial hetero-

geneity [32]. The heterogeneity of investor attitudes (optimistic–

pessimistic–neutral) undoubtedly plays a significant role in the

price movement of individual stocks and is revealed through the

trading behavior [33]. Even faced with the same historical data

of a stock, investors may hold different attitudes (someone may

be optimistic about it, someone maybe not) [34]. Investors will

show different preferences under the influence of their attitudes,

which is in favor of understanding portfolio allocation decisions.

Gupta et al. [35] also mentioned that the stock market would not

be operational if every investor had a consistent attitude towards

every asset. Based on this fact, how to integrate investor attitudes

into the portfolio selection model reasonably and effectively is

a fascinating issue and has taken on new significance in the

context of a remarkable function on behavioral finance in recent

years. Laengle et al. [36] focused on the mean–variance portfo-

lio selection model with the ordered weighted average, which

takes into account varying levels of optimism and pessimism,

thus providing a novel perspective in analyzing the attitudes

of decision-makers in the process of portfolio selection. Li and

Yi [37] developed a new fuzzy number with an adaptive index,

known as the coherent fuzzy number, which can overestimate

the membership degrees for the favorable returns and meanwhile

underestimate those for the unfavorable returns for the optimistic

investors by appropriate transformation, and reverse the trans-

formation for the pessimistic. Therefore, coherent fuzzy numbers

not only retain the advantages of traditional fuzzy numbers in

expressing and dealing with uncertainty, but also provide greater

flexibility in modeling the heterogeneity of investor attitudes in

the investment process as closely as possible. Although coherent

fuzzy numbers have more flexibility and applicability compared

with traditional fuzzy numbers, the research on portfolio selec-

tion under a coherent fuzzy environment is still in the initial

exploration stage. The models constructed in the above work [37]

are also limited to a single period of asset allocation, which is

not applicable for long-term investment and decision-making. For

the above reasons, this paper will try to introduce coherent fuzzy

numbers into the modeling of multi-period portfolio selection to

describe the possibilistic distribution of asset returns and capture

the attitude characteristics of investors.

With regard to multi-period portfolio optimization, the exist-

ing studies usually treat the risk-tolerance/expected-return level

of the whole investment horizon as a constant, that is, the risk-

tolerance/expected-return threshold in each investment period

does not vary over time. For instance, Zhang and Zhang [38] dealt

with a multi-period mean absolute deviation portfolio selection

problem considering risk control and cardinality constraints in a

fuzzy environment, where the risk control level is an invariant

constant. Mehlawat [39] discussed fuzzy multi-period portfolio

problems that integrate multi-choice aspirations for wealth and

risk respectively, in which the minimum return threshold for

each trading period is also the same. Under the credibility theory

framework, Gupta et al. [35] proposed two multi-period portfolio

optimization models using coherent fuzzy numbers, in which

portfolio risks are quantified by mean absolute semi-deviation

and Conditional Value-at-Risk. These two models show great

advantages in multiple aspects, but the risk tolerance level over

the entire investment horizon remains fixed under the same risk

measure. Furthermore, Liu and Zhang [40] formulated a fuzzy

mean-semivariance portfolio selection model based on possibility

theory, which takes the terminal wealth and cumulative risk

as the main goal of decision-making. In their model, although

the risk-tolerance and expected-return levels of each period are

inconsistent, they are given directly and full of subjectivity. Of

note, the optimal solution of the discussed portfolio selection

problems relies closely on the selection of the upper limit of risk

and the lower limit of return [41]. Considering that in the real

world, the risk-tolerance and expected-return levels are suscep-

tible to the outcomes from the portfolio in the previous period,

it is necessary to design a reasonable updating process for these

values rather than setting them statically or subjectively. Specif-

ically, if the portfolio profit in period t is larger (smaller) than

the original expectation on return, the investor will feel that

the portfolio has performed well (poorly), and then his/her risk-

tolerance level is increased (decreased) in constructing portfolios

in the following period, that is, investor is more inclined to risk-

seeking (risk aversion). According to this train of thought, Wang

et al. [42] concentrated on the problems of multi-period portfolio

selection with dynamic risk and expected-return levels in the

mean–variance frame to discuss the actual behaviors of traders

and performance of portfolios.

To the best of our knowledge, apart from the above research,

portfolio selection with dynamic risk-tolerance/expected-return

level is still uncharted territory. To supply the vacancy in this

research, this paper attempts to establish two fuzzy optimization

models subject to some realistic constraints for multi-period

portfolio selection under the coherent fuzzy environment, in

X. Gong, L. Min and C. Yu Applied Soft Computing 114 (2022) 108104

Table 1

Comparison with existing literature on portfolio selection.

Attributes Guo et al.

(2016) [30]

Liagkouras

& Metaxiotis

(2018) [31]

Zhou et al.

(2018) [34]

Zhang &

Zhang (2014)

[38]

Mehlawat

(2016) [39]

Liu & Zhang

(2015) [40]

Li and Yi

(2019) [37]

Gupta et al.

(2020) [35]

Proposed

method

Objective

functions

Linear,

non-linear

Non-linear Linear,

non-linear

Non-linear Linear Linear,

non-linear

Linear,

non-linear

Non-linear Non-linear

Environment Fuzzy Fuzzy Fuzzy Fuzzy Fuzzy Fuzzy Coherent

fuzzy

Coherent

fuzzy

Coherent

fuzzy

Investment

period

Multiple Multiple Single Multiple Multiple Multiple Single Multiple Multiple

Risk measure Fuzzy

variance

Fuzzy variance LAD Absolute

deviation

Entropy Fuzzy

semivariance

Fuzzy

variance

MASD and

CVaR

Fuzzy

variance

Fuzzy

framework

Credibilistic Possibilistic Me measure Possibilistic Credibilistic Possibilistic Possibilistic Credibilistic Possibilistic

Behavioral

factors

× × Conservative

-aggressive

× × × Optimistic–

pessimistic

Optimistic–

pessimistic

Optimistic–

pessimistic

Expected-

return level

Static Invariant Static × Invariant Variant and

given directly

Static × Dynamic

update

Risk-tolerance

level

Static × Static Invariant × Variant and

given directly

Static Invariant Dynamic

update

Transaction

cost

  ×    ×  

Full utilization

of capita

   ×     

Cardinality

constraint

×  ×    ×  

No short

selling

constraint

  × ×     

Lower–upper

bounds

constraints

× ,

upper bound

×    ×  

Number of

data set tested

Three One One One One One Two Two Two

Acronyms-LAD: Lower absolute deviation; Var-OWA: Variance-ordered weighted average; MASD: Mean absolute semi-deviation; CVaR: Conditional Value-at-Risk.

which we expend the risk-tolerance and expected-return levels to

dynamic analysis. These two multi-period portfolio models take

wealth maximization and risk minimization as objective func-

tions, respectively. The uncertainty of the proposed models and

heterogeneity of investor attitudes (optimistic, pessimistic, and

neutral) are modeled by regarding the asset returns as indepen-

dent coherent fuzzy variables. The return and risk of the asset are

quantitatively determined with the aid of the possibilistic mean

and possibilistic variance of coherent fuzzy return, respectively.

The efficient investment strategies are derived via the genetic

algorithm introduced in [40]. Table 1 provides the characteristic

comparison of our research with the existing literature on port-

folio selection. The main contributions in this study include the

following five-folds.

(i) Based on the mean–variance framework and bounded ratio-

nality of investors, we propose two coherent fuzzy multi-period

portfolio selection models, in which uncertain asset information

and the optimistic–pessimistic–neutral attitudes of investors are

characterized by coherent fuzzy numbers. (ii) We consider the

dynamic risk-tolerance and expected-return levels in portfolio

construction by designing corresponding update paths, which

offer avenues in analyzing the impact of the previous investment

results on investors’ decision behavior in the next period. (iii)

Several real-world trading constraints and transaction costs are

included in the presented models. These constraints enable our

models to simulate the stock trading storyline more realistically

and to better satisfy the diversified requirements of investors.

(iv) The empirical study with the in-sample and out-of-sample

analysis is carried out to evaluate the performance of the re-

sulting portfolios. The results on two different data sets show

that the presented models outperform the conventional ways

(static risk-tolerance and expected-return levels) on most of the

evaluation indicators. (v) In contrast to most research on this field

that considers test data between 10 and 20 stocks [39,43–45],

the data sets tested in the current study are relatively larger,

reaching 74 and 101 risky assets, respectively, thereby improving

the authenticity of the examined models.

The remainder of the current paper is structured as follows.

We first review the coherent trapezoidal fuzzy numbers in Sec-

tion 2. In Section 3, two multi-period coherent fuzzy portfolio se-

lection models with dynamic risk-tolerance and expected-return

levels are developed. In Section 4, the numerical experiments are

presented to test the proposed models. A detailed discussion of

the achieved results is also made in this section. The final section

concludes the paper.

2. Preliminaries

The financial market is a time-varying and complex system.

Its significant feature is provided with tremendous uncertainty,

which brings difficulty in accurately estimating future returns

related to assets. Fuzzy logic is considered to be an effective

and appropriate way to express ambiguity and nondeterminacy.

The membership function is the cornerstone of fuzzy set theory,

through which asset returns can be transformed into fuzzy vari-

ables for research. The coherent fuzzy number is an extended

form of traditional fuzzy number. To better understand this paper,

this section introduces the coherent trapezoidal fuzzy number.

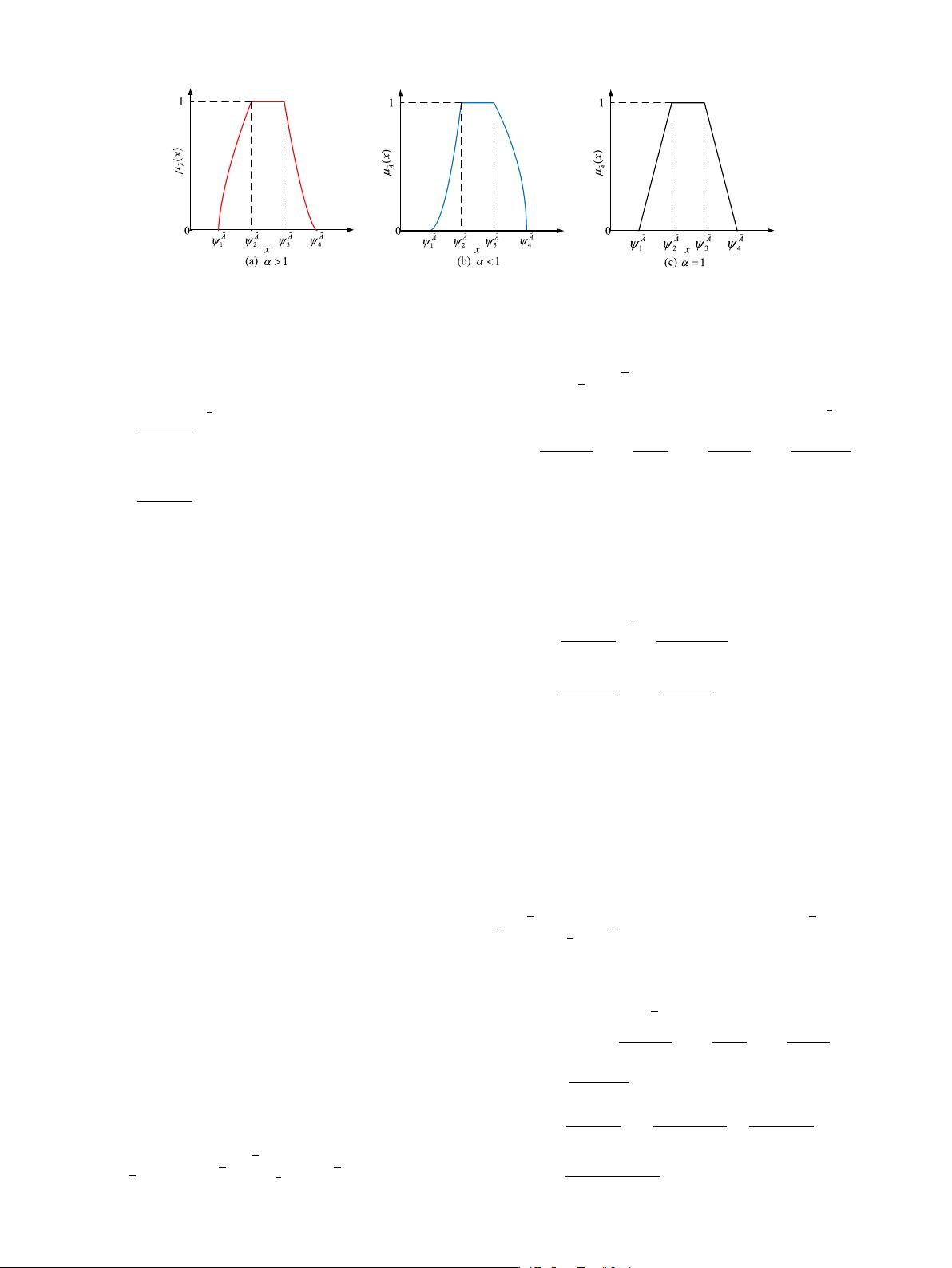
X. Gong, L. Min and C. Yu Applied Soft Computing 114 (2022) 108104

Fig. 1. Possibility distributions of

A = (ψ

, ψ

)

with α > 1, α < 1, and α = 1.

Definition 1 ([37]). A fuzzy set

A = (ψ

, ψ

)

is called

a coherent trapezoidal fuzzy number (CTrFN) with core interval

[ψ

, ψ

], left endpoint ψ

, and right endpoint ψ

. The member-

ship function of

A is denoted as µ

(x):

(x) =













x − ψ

− ψ



, ψ

< x ≤ ψ

;

1, ψ

< x ≤ ψ

;



− x

− ψ



, ψ

< x ≤ ψ

;

0, else.

(1)

where µ

(x) → [0, 1], and α is an adaptive index with α > 0.

A =

(ψ

, ψ

)

is degenerated into the coherent triangular

fuzzy number in the case of ψ

= ψ

Assuming that the future return of an asset for portfolio se-

lection is characterized by a CTrFN

A = (ψ

, ψ

)

, the

interval [ψ

, ψ

] is regarded as the most likely return on the

asset, and the intervals [ψ

, ψ

] and [ψ

, ψ

] represent the un-

favorable and favorable returns respectively. The adaptive index

α is an indicator for measuring investors’ expectations (attitudes).

According to variant values of α, we have the following three

cases: (1) When α > 1, the relatively higher membership degree

is allocated to the unfavorable returns located within [ψ

, ψ

while the relatively lower membership degree is obtained within

[ψ

, ψ

]. Therefore, α > 1 is used as a signal that reflects the

pessimistic attitude of investors (i.e., pessimistic scenario), and

a larger α value states the more pessimistic investor sentiment.

(2) When α < 1, the relatively higher membership degree is

allocated to the attractive returns located within [ψ

, ψ

], while

the returns within [ψ

, ψ

] have a smaller membership degree.

Therefore, α < 1 can be treated as a signal reflecting the op-

timistic attitude for investors (i.e., optimistic scenario), and a

smaller α value means investors are more optimistic. (3) When

α = 1, the CTrFN degenerates to the traditional trapezoidal fuzzy

number, and the linearity within [ψ

, ψ

] and [ψ

, ψ

] is a re-

flection of investor neutrality. The possibility distributions of the

CTrFN in the above three scenarios are represented graphically in

Fig. 1.

Based on Carlsson and Fullér [46], the possibilistic mean and

variance of the CTrFN can be defined as below.

Definition 2. Let

A = (ψ

, ψ

)

be a CTrFN with the

membership function µ

(x) (see Eq. (1)), the ξ − level set of

A can

be expressed as [

= [a(ξ ), a(ξ )], where a(ξ ) = ψ

+ (ψ

−

)ξ

and a(ξ ) = ψ

−(ψ

−ψ

)ξ

. Then, the possibilistic mean

A can be given by:

A) =





a(ξ) + a(ξ )



dξ





+ (ψ

− ψ

)ξ

+ ψ

− (ψ

− ψ

)ξ



dξ

2(α + 2)

α + 2

2α + 1

2(2α + 1)

(2)

Li and Yi [37] define the possibility density function of

A =

(ψ

, ψ

)

, which is stated as:

(x) = µ

(x)



′

(x)















x − ψ

− ψ



−1

k(ψ

− ψ

)

, ψ

< x < ψ

;



− x

− ψ



2α−1

− ψ

, ψ

< x < ψ

;

0, else;

(3)

where f

(x) satisfies: f

(x) ≥ 0 and



+∞

−∞

(x)dx = 1.

Based on f

(x), the possibilistic mean of

A can also be ex-

pressed as E(

A) =



+∞

−∞

(x)dx (see [37]), and the corresponding

result is the same as that of Eq. (2).

Definition 3. Let

A = (ψ

, ψ

)

be a CTrFN with the

membership function µ

(x), the ξ − level set of

A is [

[a(ξ), a(ξ )], where a(ξ ) = ψ

+ (ψ

− ψ

)ξ

and a(ξ ) = ψ

−

(ψ

− ψ

)ξ

. Then, we have the lower and upper possibilistic

semivariances of

A (Va

−

(

A) and Va

(

A)) with the following forms:

−

(

A) = 2





A) − a(ξ )



dξ

= 2





2(α + 2)

α + 2

2α + 1

2(2α + 1)



−



+ (ψ

− ψ

)ξ





dξ



− ψ



α(ψ

− ψ

)

2(α + 2)

(ψ

− ψ

)

2(2α + 1)



(ψ

− ψ

)

(α + 1)(α + 2)

(4)

剩余18页未读，继续阅读

评论收藏

内容反馈

版权申诉

pk_xz123456

粉丝: 2863
资源: 4045

金融投资组合优化中基于一致模糊环境的多期选择模型研究及其应用

论文研究-基于模糊回归分析的投资组合选择模型.pdf

基于模糊理论的组合投资模型及其应用研究1

基于优化算法的股票投资组合模型选择

模糊投资组合优化研究_陈国华1

基于累积前景理论的可变下标犹豫模糊语言多准则投资组合优化.pdf

投资组合优化模型研究1

组合投资模型及其算法研究1

论文研究-基于损失厌恶和模糊厌恶的分布鲁棒投资组合模型.pdf

几类投资组合优化模型及其算法.docx

基于鲁棒优化的若干投资组合模型研究_赵庆.caj

论文研究-带有模糊收益率的投资组合选择模型.pdf

投资组合优化模型研究_邓雪.caj

论文研究-考虑现实约束的模糊多准则投资组合优化模型.pdf

基于深度学习和进化计算的外汇预测与投资组合优化.pdf

投资组合与模糊规划模型

Python中的投资组合优化和量化战略资产配置

证券投资组合模型及其应用1

基于MATLAB的证券投资组合优化分析.pdf

均值方差投资组合模型案例（数据和MATLAB代码）.rar_matlab投资组合_mean_ori3j_投资组合_组合模型

风险投资多项目多阶段投资组合决策研究

基于高阶矩的投资组合优化研究_彭胜志.caj

基于Matlab图形用户界面的投资组合优化系统研究.pdf

最新资源