图割方法用于最大流的一片文章

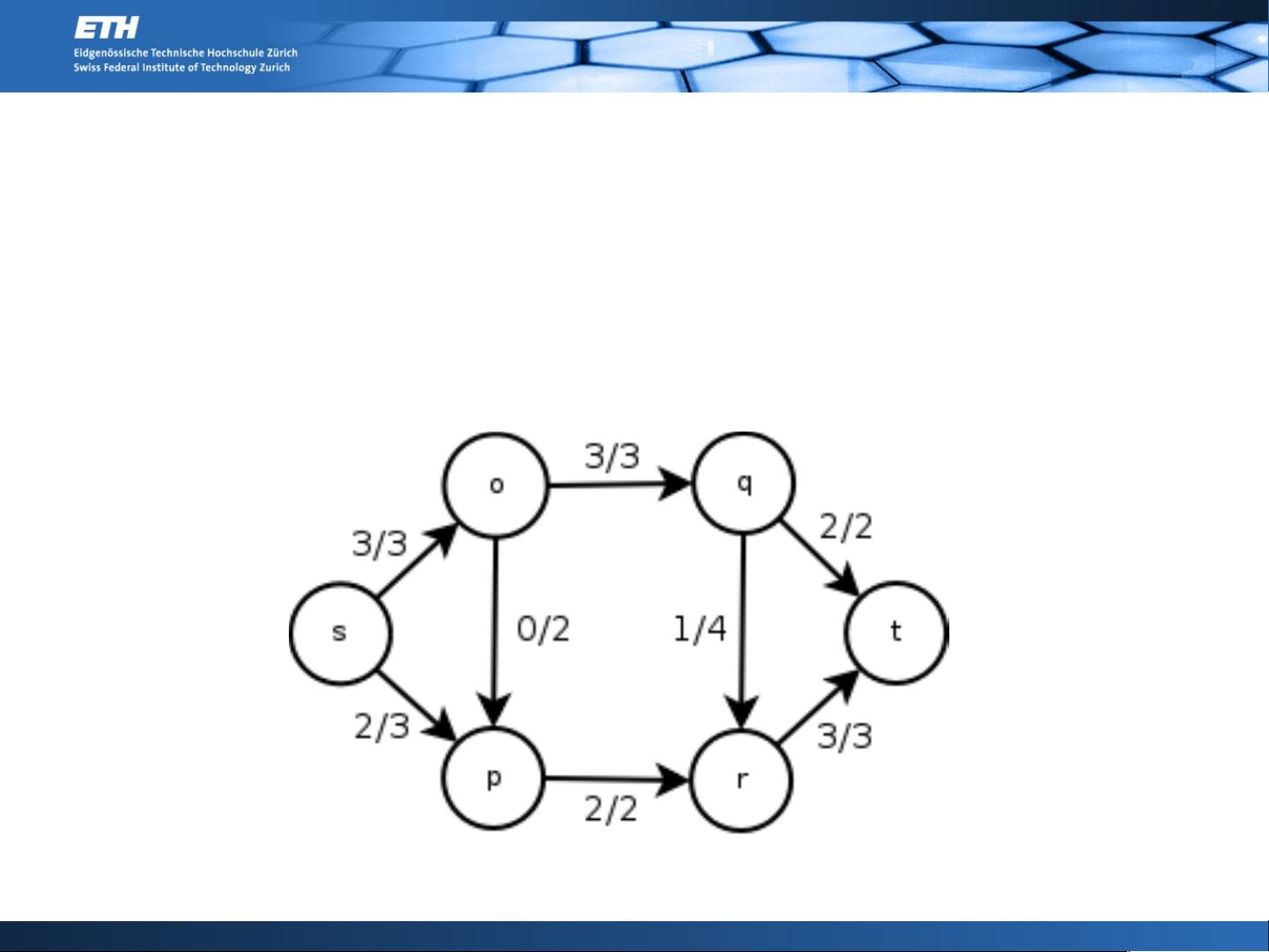
### 图割方法与最大流问题 #### 一、引言 在计算机科学和网络理论中，最大流问题(Maximum Flow Problem)是研究如何在给定的网络中寻找能够通过该网络的最大流量。这一问题有着广泛的应用场景，比如物流管理、通信网络设计、计算机视觉等。而解决最大流问题的核心算法之一就是图割方法(Mincut-Maxflow)，它不仅是一种实用的技术手段，同时也具有深刻的理论意义。 #### 二、基本概念 ##### 2.1 网络定义 一个网络可以被定义为一个四元组(G, s, t, c)，其中： - G = (V, E) 是一个有向图，包含一组顶点 V 和一组边 E。 - s 和 t 分别表示源点(source)和汇点(sink)，它们是 G 中两个不同的顶点。 - 容量函数 c: E → R 表示每条边的最大流量值。 例如，我们可以将一个网络想象成一个由单向水管组成的系统，其中每条水管都有一个特定的最大通过量。 ##### 2.2 净流出量 对于任何函数 f: E → R 和顶点 v ∈ V，净流出量 NetOut(f) 的定义如下： \[ NetOut(f) = \sum_{(v,x) \in E} f(v,x) - \sum_{(x,v) \in E} f(x,v) \] 即从 v 流出的总流量减去流入 v 的总流量。 ##### 2.3 网络流 在一个网络 (G, s, t, c) 中，任何满足以下条件的函数 f: E → R 称为网络流： - 对于每条边 e，有 \(0 \leq f(e) \leq c(e)\)。 - 对于除 s 和 t 之外的每个顶点 v，有 \(NetOut(v) = 0\)。 用更通俗的话来说，网络流就是一种容量利用率，使得除了源点 s 和汇点 t 之外的所有节点都不会有任何流量的泄漏。 #### 三、最大流问题 最大流问题是给定一个网络，找出从 s 到 t 可以通过的最大流量值以及对应的流量分配方案。换句话说，我们关心的是网络的最大传输能力及其具体的实现方式。 #### 四、s-t 割 s-t 割是指在给定的网络 (G, s, t, c) 中，所有包含 s 并且不包含 t 的顶点子集 S。s-t 割的容量 cap(S) 定义为所有从 S 中的某个节点流向 S 外部的边的容量之和。 #### 五、最大流最小割定理 最大流最小割定理指出，在任何一个网络中，最大流的值等于最小 s-t 割的容量。这个定理揭示了最大流问题的一个关键性质，也是图割方法的基础。 #### 六、残余网络 残余网络是与原网络关联的一个加权有向图，它具有相同的顶点集合，但是每条边的权重 w 表示在当前流的基础上，还可以增加的额外流量。换句话说，从 a 到 b 的一条边如果在残余网络中有权重 w，则意味着还可以从 a 向 b 增加 w 的流量。 #### 七、增广路径 增广路径是指残余网络中从 s 到 t 的一条路径，这条路径上的每条边都表明存在可以进一步增加的流量。找到这样的路径后，可以通过调整网络中的流量来得到一个新的网络流，从而逐步逼近或达到最大流。 ### 结论 图割方法是解决最大流问题的一种有效手段。通过理解基本的概念如网络、净流出量、网络流、s-t 割、最大流最小割定理以及残余网络和增广路径，我们可以更好地掌握这一领域的核心思想和技术细节。这些理论不仅有助于解决实际问题，还对深入理解计算机科学中的网络分析提供了重要的理论支持。