惯性矩计算方法及常用截面惯性矩计算公式.pdf

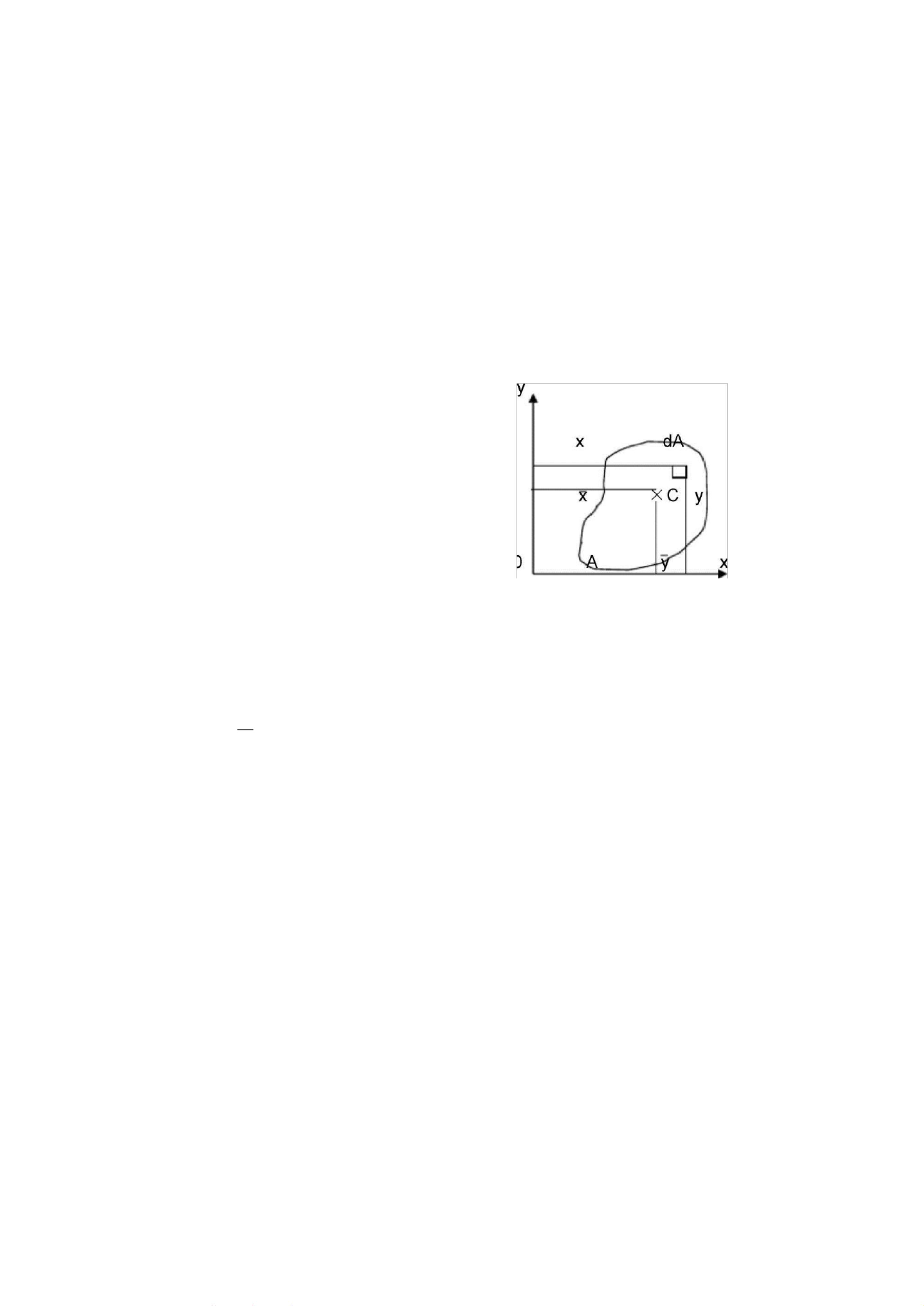
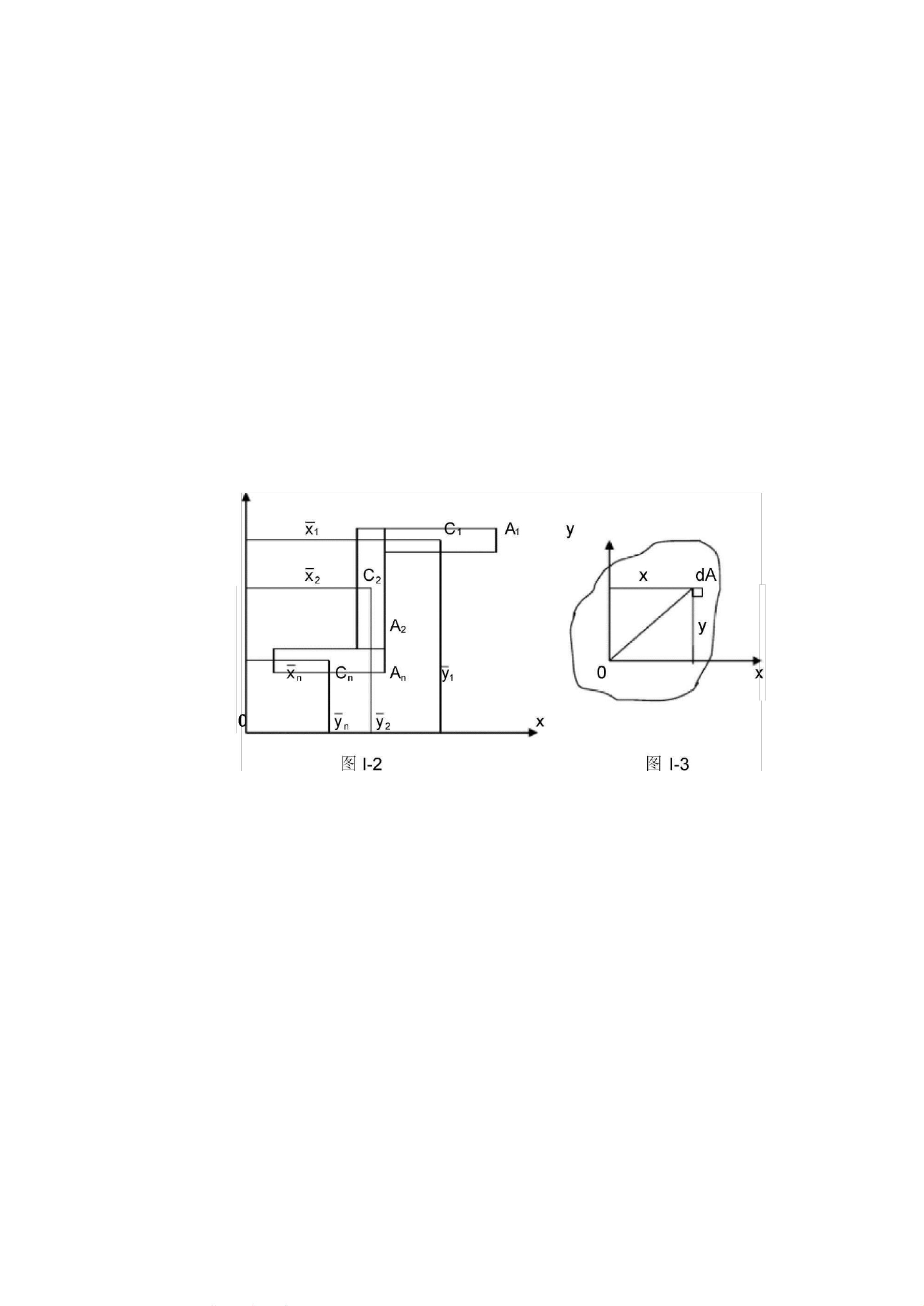
惯性矩是工程力学和结构分析中的一个重要概念，特别是在材料力学和机械设计中，用于描述物体抵抗扭动或弯曲的能力。本文将详细解释惯性矩的计算方法以及常见截面惯性矩的计算公式。 我们要理解的是截面静矩的概念。截面静矩，又称为面积矩，是衡量平面图形对某一轴线的分布情况的几何性质。它是通过将图形分割成无数小面积元素，然后计算每个元素到该轴线距离的平方乘以其面积的积分。对于任意有限平面图形，静矩的定义式为：dSy = x * dA 和 dSx = y * dA，其中dA是面积元素，x和y是元素中心点相对于轴线的距离。整个图形对y轴和z轴的静矩分别表示为Sy = ∫xdA和Sx = ∫ydA。 形心是图形面积的平均位置，它的坐标可以通过静矩来确定。若图形形心的坐标为(yC, zC)，则有0 = ∑Sx/A 和 0 = ∑Sy/A。如果y轴通过形心，则静矩Sy = 0；同样，如果x轴通过形心，则Sx = 0。如果x、y轴都是图形的对称轴，那么它们的交点就是图形的形心；如果y轴是图形的对称轴，形心必定位于此轴上。对于组合图形，静矩和形心可以通过各部分图形的静矩和形心坐标进行加权求和。 接下来，我们讨论惯性矩。惯性矩是衡量截面图形旋转惯性的量，分为极惯性矩和轴惯性矩。极惯性矩I_p是关于某一点O的，定义为图形面积A与所有面积元素到点O的平方距离的积分，即I_p = A * ∫(2dA)。而轴惯性矩是关于坐标轴的，例如，对于y轴的轴惯性矩I_y = ∫x^2dA，x轴的轴惯性矩I_x = ∫y^2dA。惯性矩的特性包括：它与定义点或轴有关，单位是m^4，数值始终为正，且图形对某点的极惯性矩等于对以该点为原点的任意一对坐标轴的轴惯性矩之和。 对于组合图形，其极惯性矩或轴惯性矩等于各部分图形的相应惯性矩的和。惯性积（惯性矩的乘积）也是分析截面性质的重要参数，用于描述截面对扭转和弯曲的抵抗能力。惯性半径则是基于惯性矩计算的，它描述了截面抗弯性能的一个关键指标。 在实际应用中，如建筑设计、桥梁结构、机械零件设计等，常常需要根据特定截面形状计算相应的惯性矩，以便进行强度分析和稳定性评估。常见的截面如矩形、圆形、工字梁截面等都有各自的惯性矩计算公式，这些公式通常涉及到几何参数，如宽度、高度、半径等，并通过积分或已知公式直接求解。 总结起来，惯性矩计算是分析截面力学性能的基础，涉及静矩、形心、极惯性矩、轴惯性矩等多个概念。理解和熟练掌握这些计算方法对于工程实践至关重要。