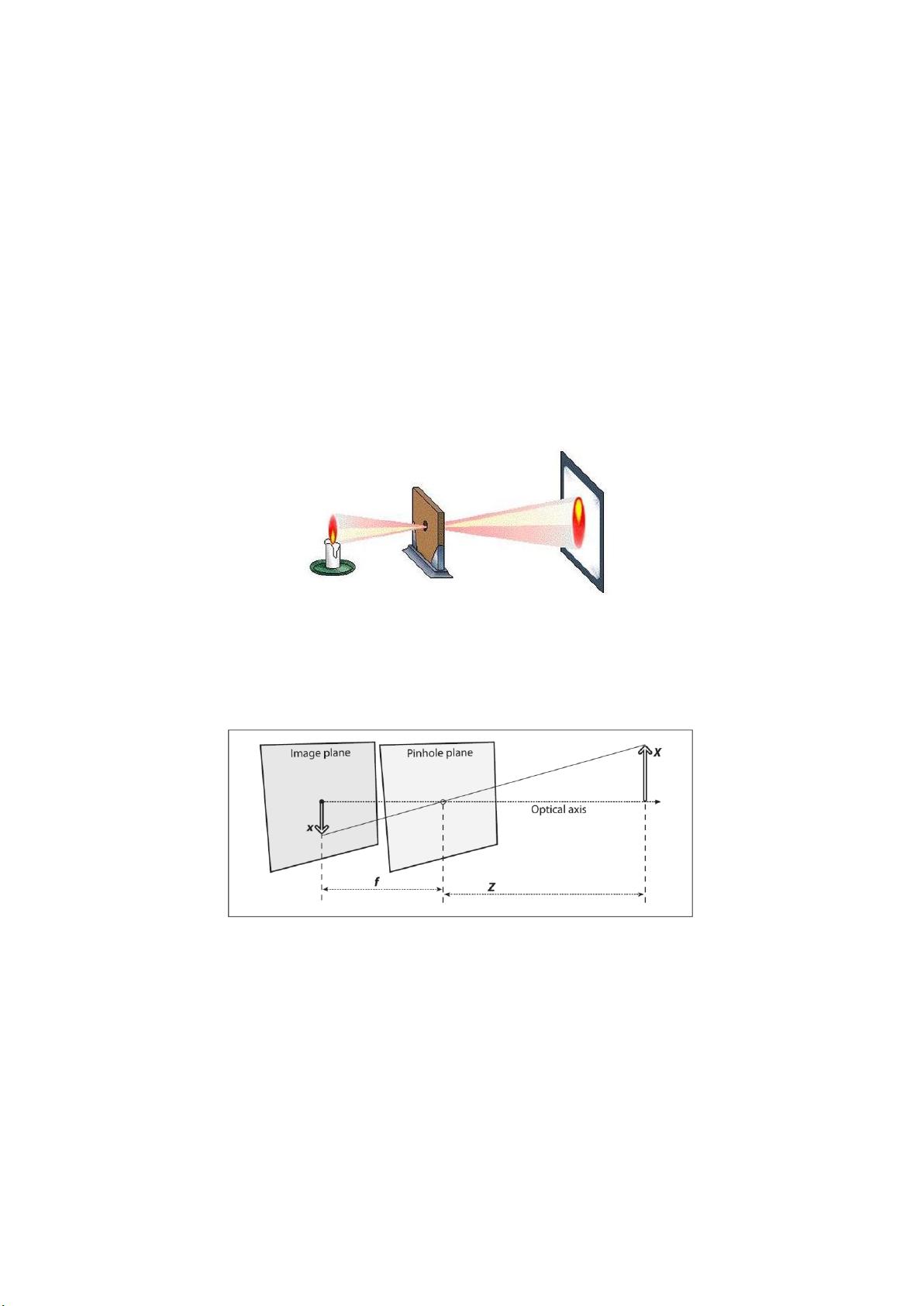
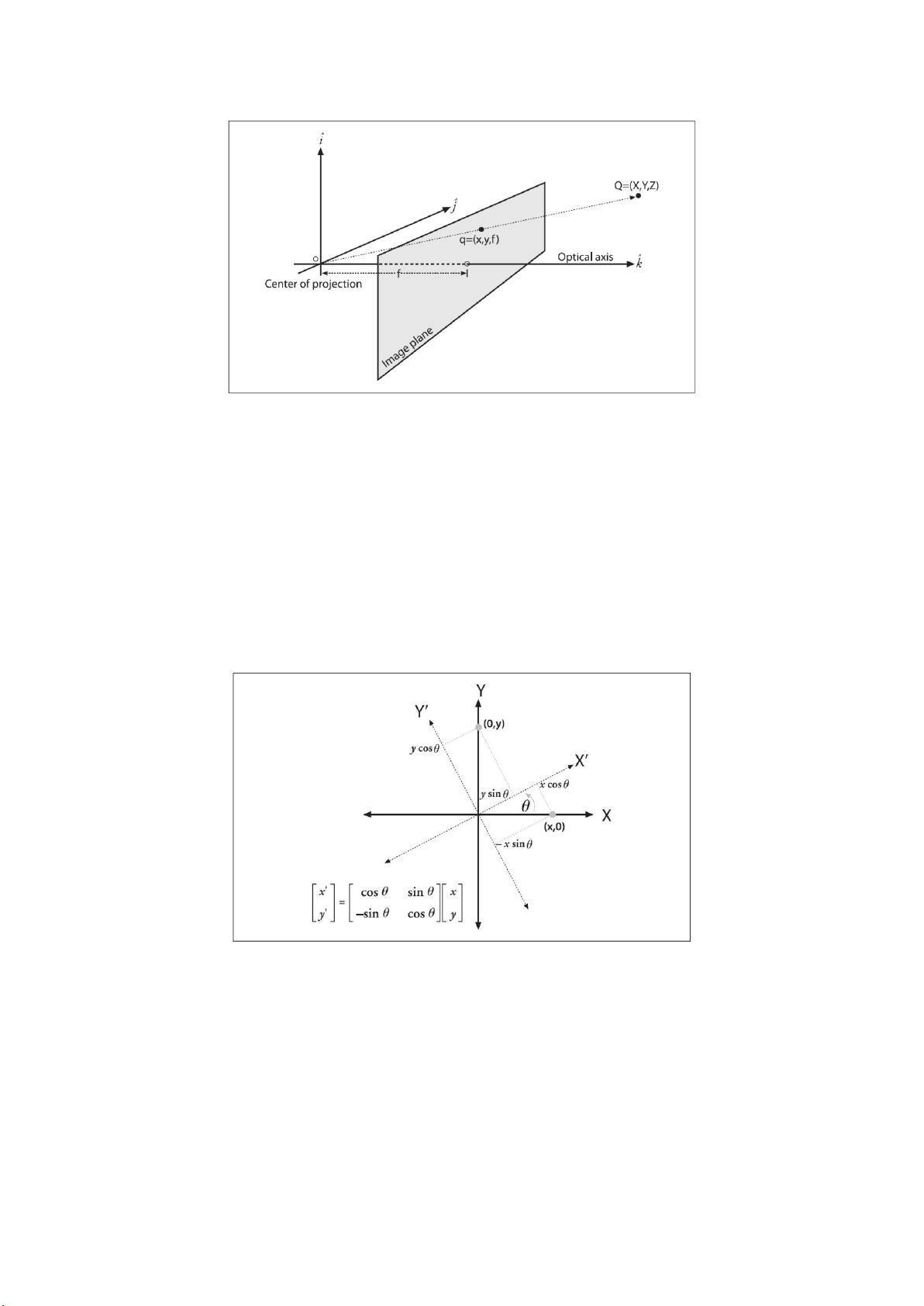
halcon相机标定

### Halcon相机标定知识点详解 #### 一、相机标定基本原理 ##### 1.1 相机成像模型 在计算机视觉领域，相机标定是一项基础且重要的技术，其目的是确定相机内部参数（如焦距、图像传感器尺寸等）和外部参数（如相机在世界坐标系中的位置和姿态）。基于不同的成像原理和技术，相机模型可以分为多种类型，其中最为常见的两种是基于针孔成像原理的模型和基于光线追踪法的模型。 - **针孔成像原理**：这是一种简单的物理模型，通过一个小孔来模拟光线如何从物体传递到成像面上。针孔模型能够很好地解释相机的基本工作原理，但由于它是一个理想化的模型，并未考虑实际相机的各种物理特性（如镜头尺寸、偏斜等），因此在精度上有一定的局限性。 - **歪斜光线追踪法与近轴光线追踪法**：这两种方法更适用于复杂场景下的成像模拟，尤其是在需要高精度成像的情况下。通过精确计算光线路径及其与物体表面的相互作用，可以更准确地模拟真实世界的成像效果。 ##### 1.2 坐标系间的转换 相机标定过程中涉及多个坐标系的转换，这些转换是实现准确标定的基础。 - **世界坐标系**：这是一个固定的三维坐标系，用于描述真实世界中物体的位置。 - **相机坐标系**：以相机镜头中心为原点建立的坐标系，通常以相机的光轴作为Z轴方向。 - **图像坐标系**：包括图像物理坐标系和图像像素坐标系，用于描述成像后图像上的像素位置。 **从世界坐标系到相机坐标系**的转换涉及到旋转和平移操作。旋转操作可以通过构建旋转矩阵来完成，而平移则通过平移向量来表示。旋转矩阵由三个基本旋转矩阵相乘得到，每个矩阵对应绕X、Y和Z轴的旋转。 - **旋转矩阵**：根据旋转角度，可以构建出围绕各个轴的旋转矩阵。例如，围绕X轴旋转的矩阵为\[R_x = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos(\alpha) & -\sin(\alpha) \\ 0 & \sin(\alpha) & \cos(\alpha) \end{bmatrix}\]。 - **平移矩阵**：表示为\[T = [t_x, t_y, t_z]\]，其中\(t_x, t_y, t_z\)是世界坐标系原点与相机坐标系原点之间的相对位置。 **从相机坐标系到图像坐标系**的转换涉及透视投影。透视投影通过公式\[X_d = f \cdot \frac{X_c}{Z_c}, Y_d = f \cdot \frac{Y_c}{Z_c}\]来完成，这里\(f\)表示焦距，\(X_c, Y_c, Z_c\)是相机坐标系中的点，而\(X_d, Y_d\)则是图像坐标系中的点。 **从图像物理坐标系到图像像素坐标系**的转换主要是为了方便后续处理。通常使用\(X_f = X_d/d_x + C_x, Y_f = Y_d/d_y + C_y\)来进行转换，其中\(d_x, d_y\)代表相邻像素点之间的物理距离，而\(C_x, C_y\)则是图像物理坐标系原点在图像像素坐标系中的坐标。 #### 二、相机畸变模型 相机畸变是指由于镜头本身的特性导致图像出现变形的现象。畸变主要包括两种类型：径向畸变和切向畸变。 - **径向畸变**：由透镜造成的畸变，主要表现为图像边缘部分的放大或缩小。这种畸变可以通过调整径向畸变系数来校正，常见的一阶或二阶径向畸变校正模型为：\[X_u = X_d + X_d(k_1r^2 + k_2r^4 + \cdots), Y_u = Y_d + Y_d(k_1r^2 + k_2r^4 + \cdots)\]，其中\(k_1, k_2, \cdots\)为径向畸变系数，\(r = \sqrt{X_d^2 + Y_d^2}\)。 - **切向畸变**：由成像仪与相机透镜之间的不平行性引起，表现为图像中物体的倾斜。切向畸变的校正模型为：\[X_u = X_d + P_1X_d(3X_d^2 + Y_d^2) + 2P_2X_dY_d + O[(X_d, Y_d)^4], Y_u = Y_d + P_2X_d(3X_d^2 + Y_d^2) + 2P_1X_dY_d + O[(X_d, Y_d)^4]\]，其中\(P_1, P_2\)为切向畸变系数。 通过以上分析可以看出，相机标定不仅需要理解相机的工作原理和不同坐标系之间的转换，还需要了解并解决由镜头引起的畸变问题。这对于确保图像处理结果的准确性至关重要。Halcon软件提供了一系列工具和函数来支持相机标定任务，使得用户能够高效地进行相机标定和畸变校正。