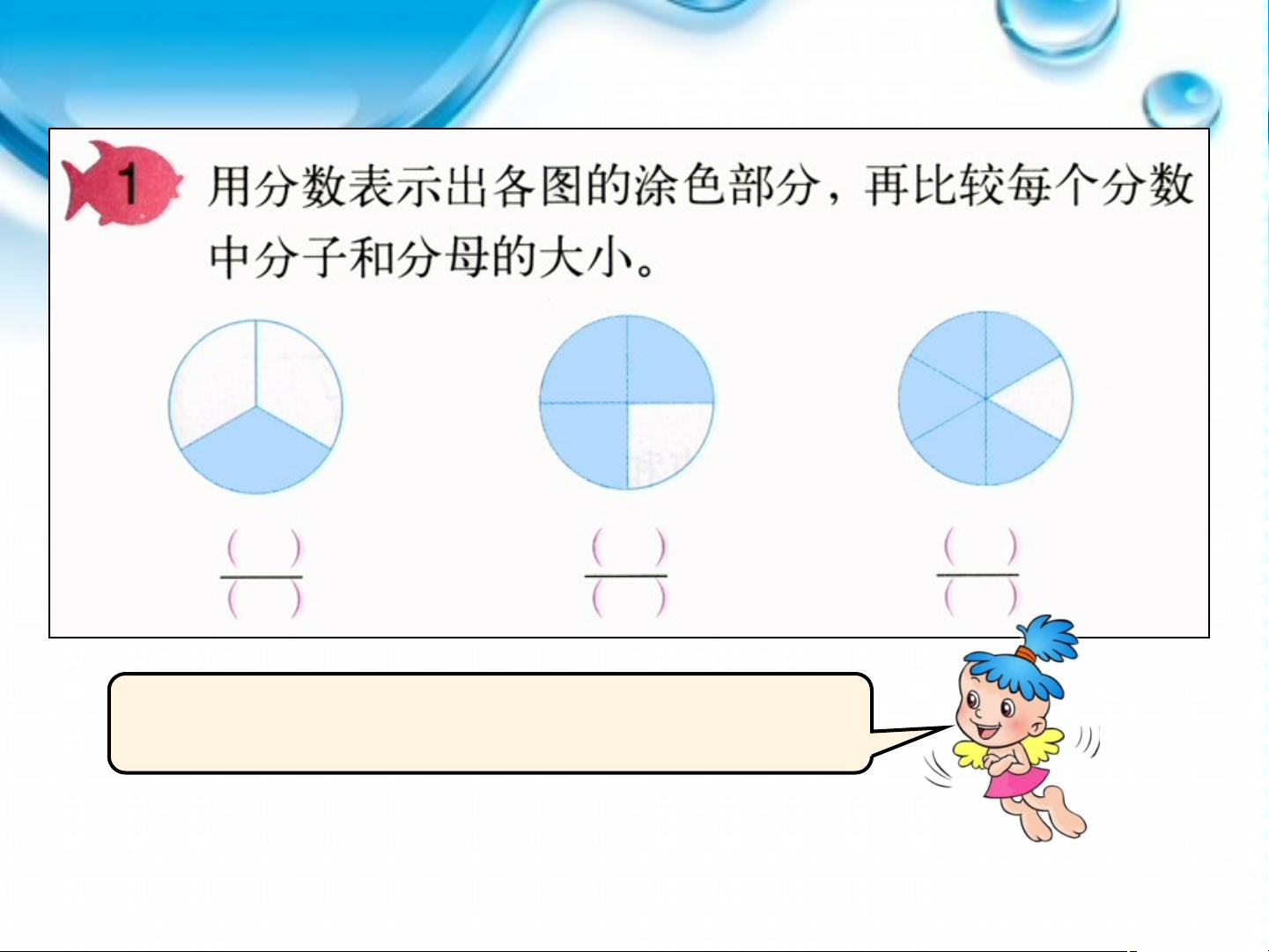
在数学的分数概念中,真分数和假分数是两种重要的分数类型。它们主要根据分子与分母的关系来定义。理解这两个概念对于学习更高级的代数和几何概念至关重要。
我们来定义真分数。一个分数如果其分子比分母小,那么这个分数被称为真分数。例如,题目中给出的2/3、5/6、7/34等都是真分数。真分数的数值总是小于1,因为分子代表的部分小于分母代表的整体。在数轴上,真分数位于0和1之间。
假分数则有所不同。假分数是指分子比分母大或者分子与分母相等的分数。比如,3/2、33/3、5/3等都是假分数。假分数可以表示为大于或等于1的数值。当假分数的分子等于分母时,它实际上是整数1。
题目中还有一些关于真分数和假分数的判断题。例如,"假分数都比1大"这个说法是错误的,因为当分子等于分母时,假分数等于1。而"分母比分子大的分数是真分数"这个陈述是正确的,符合真分数的定义。"假分数的分子不小于分母"也是正确的,这正是假分数的特征。
在实际应用中,我们经常需要将分数表示在数轴上。真分数位于数轴的0到1之间,假分数则位于1或1以上的区域。题目中的练习要求将分数在直线上表示出来,这对于理解分数的大小关系很有帮助。
此外,题目还涉及到找特定条件下的分数。例如,写出分母为8的所有真分数和假分数。分母为8的真分数有无限多个,它们是从1/8到7/8的连续分数。最大的真分数是7/8,最小的是1/8。而分子为8的假分数则是8/8,8/4,8/3,8/2等,一直到8/1(等于8)。
分数单位的概念也很重要,它是构成分数的基本部分。例如,分数单位是1/8的最大真分数是7/8,最小假分数是8/8。一个分数可以看作是若干个分数单位的组合,比如3/4可以表示为3个1/4的组合。
题目还提到了找分母是2、3、4、5的真分数的个数。分母为2的真分数有1个(1/2),分母为3的有2个(1/3,2/3),分母为4的有3个(1/4,2/4,3/4),分母为5的有4个(1/5,2/5,3/5,4/5)。可以看出,对于任意正整数n,分母为n的真分数个数是n-1个。这种关系也适用于分母为6和10的情况,分别是5个和9个真分数。
总结一下,真分数和假分数是分数系统中的基础概念,它们在数学运算和解题中扮演着关键角色。通过比较分子和分母,我们可以识别和操作这些分数,从而解决各种数学问题。理解真分数和假分数的性质及其相互转换,对于深入学习分数和代数具有重要意义。