没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

第十章上机实验
1
第十章 上机实验
数字信号处理是一门理论和实际密切结合的课程,为深入掌握课程内容,最好在学习理
论的同时,做习题和上机实验。上机实验不仅可以帮助读者深入的理解和消化基本理论,而
且能锻炼初学者的独立解决问题的能力。本章在第二版的基础上编写了六个实验,前五个实
验属基础理论实验,第六个属应用综合实验。
实验一 系统响应及系统稳定性。
实验二 时域采样与频域采样。
实验三 用 FFT 对信号作频谱分析。
实验四 IIR 数字滤波器设计及软件实现。
实验五 FIR 数字滤波器设计与软件实现
实验六 应用实验——数字信号处理在双音多频拨号系统中的应用
任课教师根据教学进度,安排学生上机进行实验。建议自学的读者在学习完第一章后作
实验一;在学习完第三、四章后作实验二和实验三;实验四 IIR 数字滤波器设计及软件实现
在。学习完第六章进行;实验五在学习完第七章后进行。实验六综合实验在学习完第七章或
者再后些进行;实验六为综合实验,在学习完本课程后再进行。
function tstem(xn,yn)
%时域序列绘图函数
% xn:信号数据序列,yn:绘图信号的纵坐标名称(字符串)
n=0:length(xn)-1;
stem(n,xn,'.');box on
xlabel('n');ylabel(yn);
axis([0,n(end),min(xn),1.2*max(xn)])
10.1 实验一: 系统响应及系统稳定性
1.实验目的
(1)掌握求系统响应的方法。
(2)掌握时域离散系统的时域特性。
(3)分析、观察及检验系统的稳定性。
2.实验原理与方法
在时域中,描写系统特性的方法是差分方程和单位脉冲响应,在频域可以用系统函数
描述系统特性。已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输
入信号的响应,本实验仅在时域求解。在计算机上适合用递推法求差分方程的解,最简单的
方法是采用 MATLAB 语言的工具箱函数 filter 函数。也可以用 MATLAB 语言的工具箱函数
conv 函数计算输入信号和系统的单位脉冲响应的线性卷积,求出系统的响应。
系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。重点分析实验系统
的稳定性,包括观察系统的暂态响应和稳定响应。
系统的稳定性是指对任意有界的输入信号,系统都能得到有界的系统响应。或者系统
的单位脉冲响应满足绝对可和的条件。系统的稳定性由其差分方程的系数决定。
实际中检查系统是否稳定,不可能检查系统对所有有界的输入信号,输出是否都是有

第十章上机实验
2
界输出,或者检查系统的单位脉冲响应满足绝对可和的条件。可行的方法是在系统的输入端
加入单位阶跃序列,如果系统的输出趋近一个常数(包括零),就可以断定系统是稳定的
[19]
。系统的稳态输出是指当
��n
时,系统的输出。如果系统稳定,信号加入系统后,系
统输出的开始一段称为暂态效应,随 n 的加大,幅度趋于稳定,达到稳态输出。
注意在以下实验中均假设系统的初始状态为零。
3.实验内容及步骤
(1)编制程序,包括产生输入信号、单位脉冲响应序列的子程序,用 filter 函数或 conv
函数求解系统输出响应的主程序。程序中要有绘制信号波形的功能。
(2)给定一个低通滤波器的差分方程为
)1(9.0)1(05.0)(05.0)( ����� nynxnxny
输入信号
)()(
81
nRnx �
)()(
2
nunx �
a) 分别求出系统对
)()(
81
nRnx �
和
)()(
2
nunx �
的响应序列,并画出其波形。
b) 求出系统的单位冲响应,画出其波形。
(3)给定系统的单位脉冲响应为
)()(
101
nRnh �
)3()2(5.2)1(5.2)()(
2
������� nnnnnh
����
用线性卷积法分别求系统 h
1
(n)和 h
2
(n)对
)()(
81
nRnx �
的输出响应,并画出波形。
(4)给定一谐振器的差分方程为
)2()()2(9801.0)1(8237.1)(
00
������� nxbnxbnynyny
令
49.100/1
0
�b
,谐振器的谐振频率为 0.4rad。
a) 用实验方法检查系统是否稳定。输入信号为
)(nu
时,画出系统输出波形。
b) 给定输入信号为
)4.0sin()014.0sin()( nnnx ��
求出系统的输出响应,并画出其波形。
4.思考题
(1) 如果输入信号为无限长序列,系统的单位脉冲响应是有限长序列,可否用线性卷积
法求系统的响应? 如何求?
(2)如果信号经过低通滤波器,把信号的高频分量滤掉,时域信号会有何变化,用前面
第一个实验结果进行分析说明。
5.实验报告要求
(1)简述在时域求系统响应的方法。
(2)简述通过实验判断系统稳定性的方法。分析上面第三个实验的稳定输出的波形。

第十章上机实验
3
(3)对各实验所得结果进行简单分析和解释。
(4)简要回答思考题。
(5)打印程序清单和要求的各信号波形。
10.1.2 实验程序清单
%实验 1:系统响应及系统稳定性
close all;clear all
%======内容 1:调用 filter 解差分方程,由系统对 u(n)的响应判断稳定性======
A=[1,-0.9];B=[0.05,0.05]; %系统差分方程系数向量 B 和 A
x1n=[1 1 1 1 1 1 1 1 zeros(1,50)]; %产生信号 x1(n)=R8(n)
x2n=ones(1,128); %产生信号 x2(n)=u(n)
hn=impz(B,A,58); %求系统单位脉冲响应 h(n)
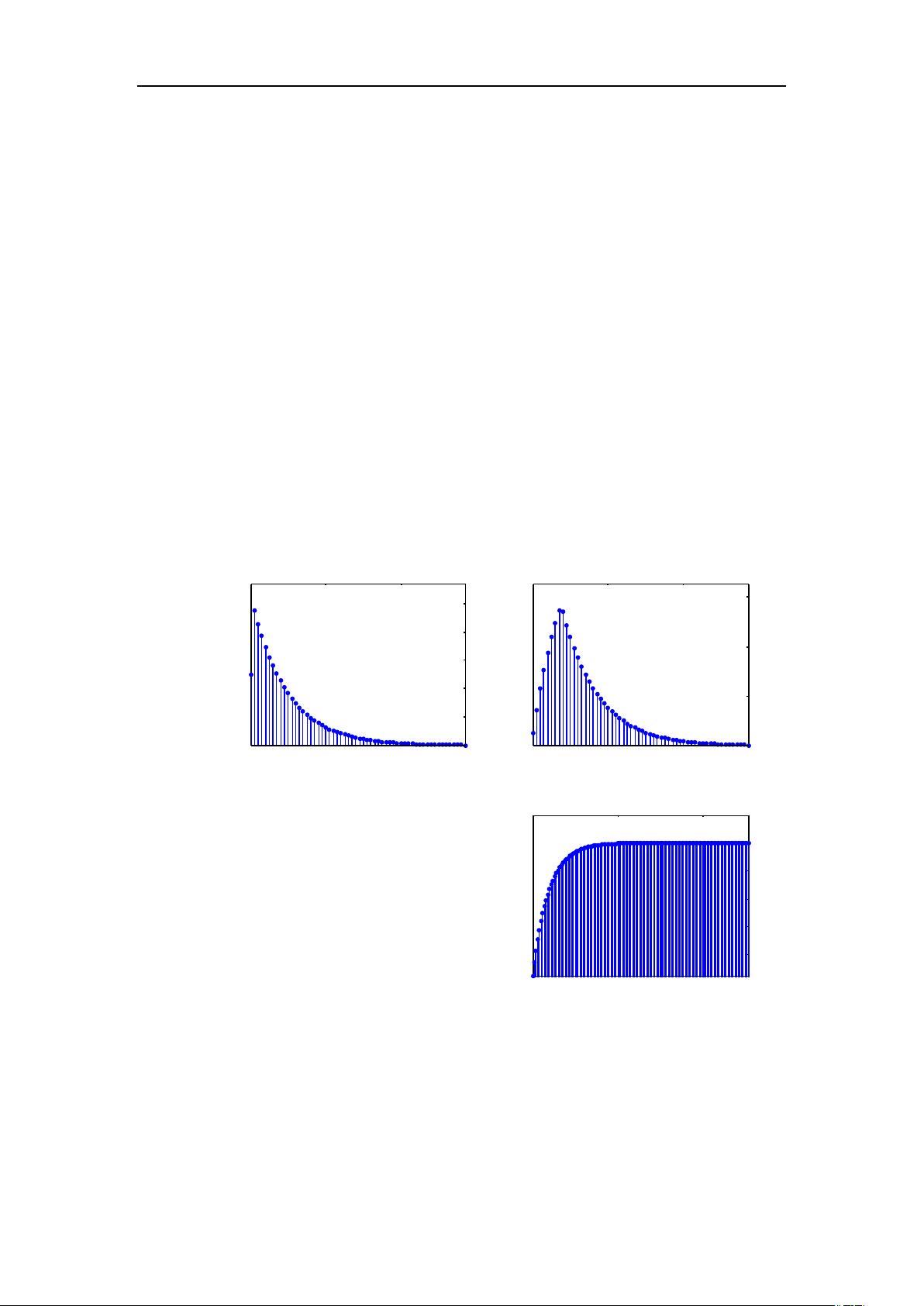
subplot(2,2,1);y='h(n)';tstem(hn,y); %调用函数 tstem 绘图
title('(a) 系统单位脉冲响应 h(n)');box on
y1n=filter(B,A,x1n); %求系统对 x1(n)的响应 y1(n)
subplot(2,2,2);y='y1(n)';tstem(y1n,y);
title('(b) 系统对 R8(n)的响应 y1(n)');box on
y2n=filter(B,A,x2n); %求系统对 x2(n)的响应 y2(n)
subplot(2,2,4);y='y2(n)';tstem(y2n,y);
title('(c) 系统对 u(n)的响应 y2(n)');box on
%===内容 2:调用 conv 函数计算卷积============================
x1n=[1 1 1 1 1 1 1 1 ]; %产生信号 x1(n)=R8(n)
h1n=[ones(1,10) zeros(1,10)];
h2n=[1 2.5 2.5 1 zeros(1,10)];
y21n=conv(h1n,x1n);
y22n=conv(h2n,x1n);
figure(2)
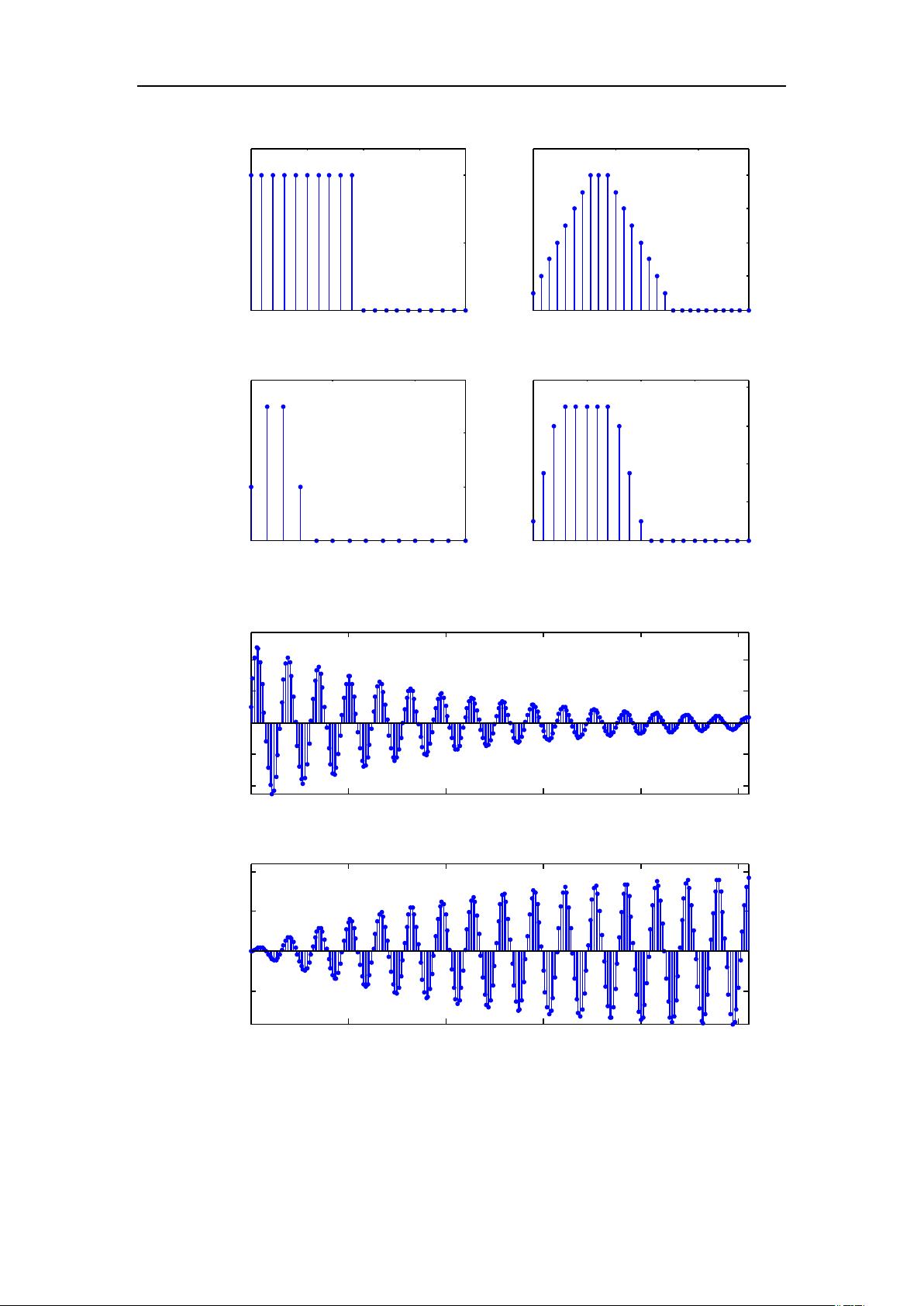
subplot(2,2,1);y='h1(n)';tstem(h1n,y); %调用函数 tstem 绘图
title('(d) 系统单位脉冲响应 h1(n)');box on
subplot(2,2,2);y='y21(n)';tstem(y21n,y);
title('(e) h1(n)与 R8(n)的卷积 y21(n)');box on
subplot(2,2,3);y='h2(n)';tstem(h2n,y); %调用函数 tstem 绘图
title('(f) 系统单位脉冲响应 h2(n)');box on
subplot(2,2,4);y='y22(n)';tstem(y22n,y);
title('(g) h2(n)与 R8(n)的卷积 y22(n)');box on
%=========内容 3:谐振器分析========================
un=ones(1,256); %产生信号 u(n)
n=0:255;
xsin=sin(0.014*n)+sin(0.4*n); %产生正弦信号
A=[1,-1.8237,0.9801];B=[1/100.49,0,-1/100.49]; %系统差分方程系数向量 B 和 A
y31n=filter(B,A,un); %谐振器对 u(n)的响应 y31(n)
y32n=filter(B,A,xsin); %谐振器对 u(n)的响应 y31(n)
figure(3)
subplot(2,1,1);y='y31(n)';tstem(y31n,y);
第十章上机实验
4
title('(h) 谐振器对 u(n)的响应 y31(n)');box on
subplot(2,1,2);y='y32(n)';tstem(y32n,y);
title('(i) 谐振器对正弦信号的响应 y32(n)');box on
10.1.3 实验程序运行结果及分析讨论
程序运行结果如图 10.1.1 所示。
实验内容(2)系统的单位冲响应、系统对
)()(
81
nRnx �
和
)()(
2
nunx �
的响应序列
分别如图(a)、(b)和(c)所示;
实验内容(3)系统 h
1
(n)和 h
2
(n)对
)()(
81
nRnx �
的输出响应分别如图(e)和(g)所示;
实验内容(4)系统对
)(nu
和
)4.0sin()014.0sin()( nnnx ��
的响应序列分别如图(h)和
(i)所示。由图(h)可见,系统对
)(nu
的响应逐渐衰减到零,所以系统稳定。由图(i)可见,系
统对
)4.0sin()014.0sin()( nnnx ��
的稳态响应近似为正弦序列
sin(0.4 )n
,这一结论验
证了该系统的谐振频率是 0.4 rad。
0 20 40
0.02
0.04
0.06
0.08
0.1
n
h(n)
(a) 系 统 单 位 脉 冲 响 应 h(n)
0 20 40
0.2
0.4
0.6
n
y1(n)
(b) 系 统 对 R8(n)的 响 应 y1(n)
0 50 100
0.2
0.4
0.6
0.8
1
n
y2(n)
(c) 系 统 对 u(n)的 响 应 y2(n)
第十章上机实验
5
图 10.1.1
10.1.4 简答思考题
(1) 如果输入信号为无限长序列,系统的单位脉冲响应是有限长序列,可否用线性卷积
0 5 10 15
0
0.5
1
n
h1(n)
(d) 系 统 单 位 脉 冲 响 应 h1(n)
0 10 20
0
2
4
6
8
n
y21(n)
(e) h1(n)与 R8(n)的 卷 积 y21(n)
0 5 10
0
1
2
3
n
h2(n)
(f) 系 统 单 位 脉 冲 响 应 h2(n)
0 5 10 15 20
0
2
4
6
8
n
y22(n)
(g) h2(n)与 R8(n)的 卷 积 y22(n)
0 50 100 150 200 250
-0.04
-0.02
0
0.02
0.04
n
y31(n)
(h) 谐 振 器 对 u(n)的 响 应 y31(n)
0 50 100 150 200 250
-0.5
0
0.5
1
n
y32(n)
(i) 谐 振 器 对 正 弦 信 号 的 响 应 y32(n)
剩余40页未读,继续阅读
资源评论

文档优选
- 粉丝: 95
- 资源: 1万+
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功