最全的运筹学复习题及答案.pdf

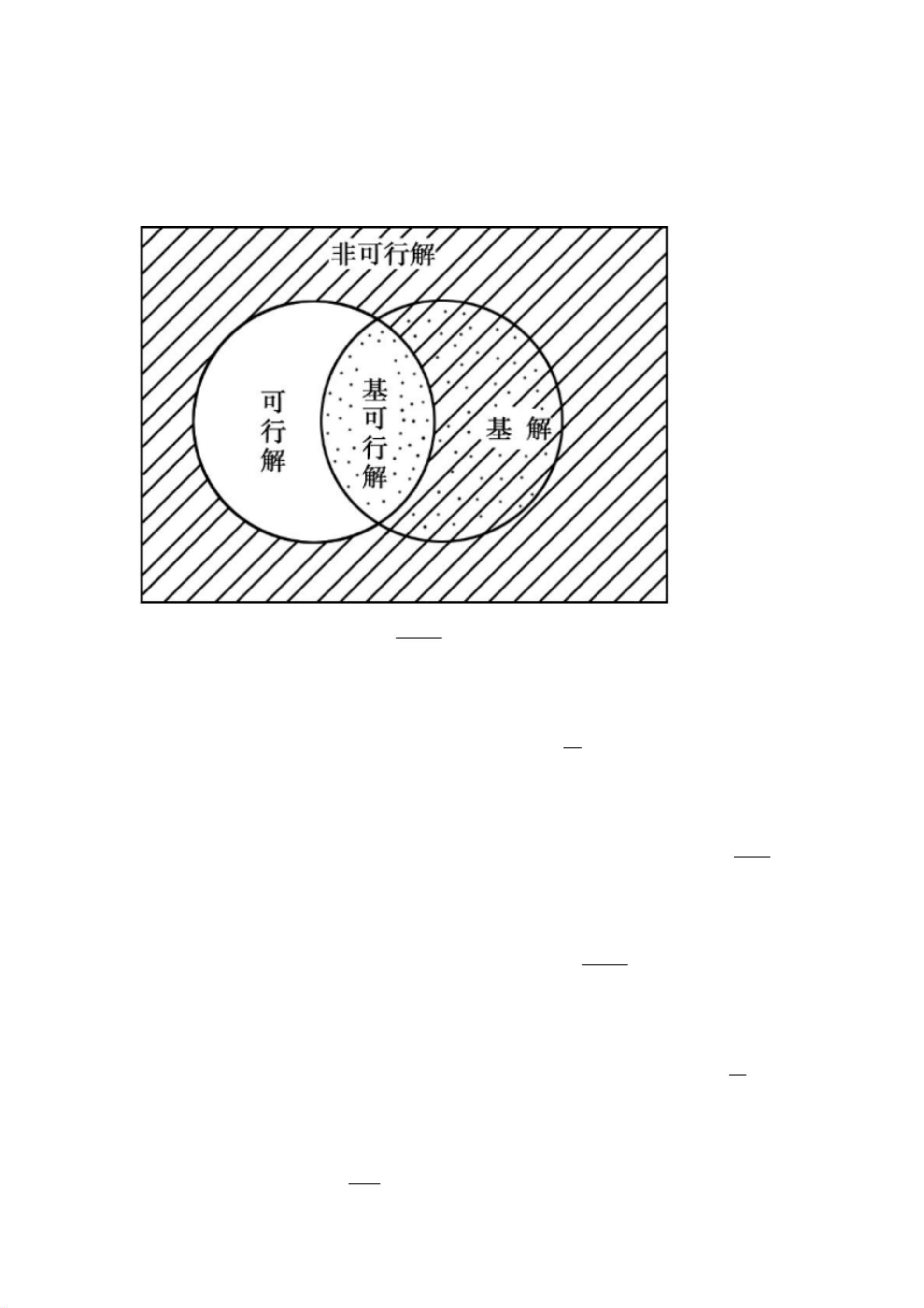
运筹学是一门应用数学的分支，它使用数学模型、统计分析和算法等工具来解决复杂的决策问题。运筹学在很多领域都有广泛的应用，如物流、管理、工业工程、商业、军事等。本文件提到的复习题及答案覆盖了运筹学中多个核心概念，包括线性规划、单纯形法、对偶理论与原理、影子价格、整数规划、旅行商问题（TSP）、列生成、图与网络模型、最小代价流网络、关键路径、最短路径以及对策论和动态规划等。 线性规划是运筹学中最为基本和广泛使用的技术之一，它关注的是在给定一组线性约束条件下，如何寻找最优解以最大化或最小化某个线性目标函数。单纯形法是解决线性规划问题的一种常用算法，它通过迭代来不断改进解，直到找到最优解。对偶理论与原理是线性规划的另一重要组成部分，它提供了一种通过构造一个对偶问题来简化原问题的方法，并有助于理解和解决原问题。 影子价格是指在对偶问题中，约束条件的右侧常数项的增加对原问题最优目标函数值的影响。影子价格的概念在经济学中具有重要意义，因为它可以作为资源定价和决策的依据。 整数规划是线性规划的扩展，它要求决策变量取整数值。由于整数规划问题通常比相应的线性规划问题更难解决，因此提出了很多启发式和近似算法来求解整数规划问题。 旅行商问题（TSP）是组合优化中一个著名的问题，目标是在一系列城市中找到一条最短的路径，每个城市恰好访问一次并返回起点。列生成是一种解决大规模线性规划问题的方法，特别是当变量数量非常庞大时，通过迭代过程逐步增加变量（列）来找到最优解。 图与网络模型是运筹学中用来描述和解决与网络结构相关的问题的一种模型。在图模型中，顶点表示实体，边表示实体之间的关系。图论中的一些重要概念，比如最小代价流网络、关键路径和最短路径等，都可以用来解决实际问题。 最小代价流网络关注的是如何在给定的网络中找到最小化总成本的最大流量问题。关键路径是项目管理中用来识别项目中最重要的活动序列的方法，它决定了完成项目所需的最短时间。 最短路径问题是在图中找到两个顶点之间的最短路径，这是一个在计算机科学和网络设计中常见问题。对于有向图和无向图，都有多种算法可以求解，如迪杰斯特拉算法和贝尔曼-福特算法等。 对策论（又称博弈论）是研究具有冲突和合作特性的决策制定者（即“玩家”）之间的战略互动的数学理论。它在经济学、国际关系、军事战略、竞争性游戏等领域都有应用。 动态规划是一种通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。它通常用于求解具有重叠子问题和最优子结构的问题，如背包问题和多阶段决策过程。 以上概念是运筹学的基础知识点，它们之间既有联系也有区别。掌握这些知识点，对于深入学习运筹学以及在实际工作中运用运筹学解决问题是非常重要的。