数学建模-最小生成树-kruskal算法及各种代码之欧阳道创编.docx

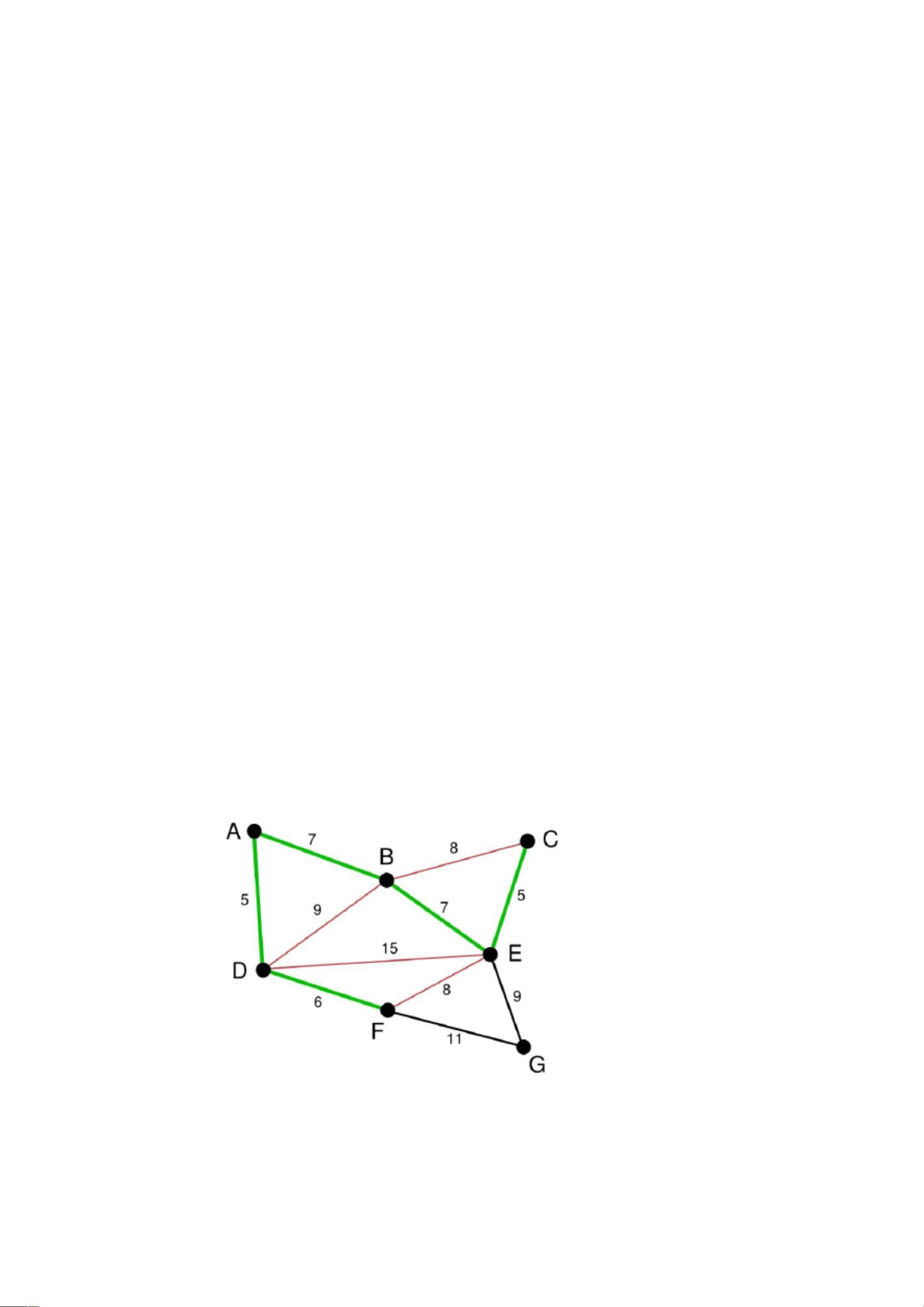
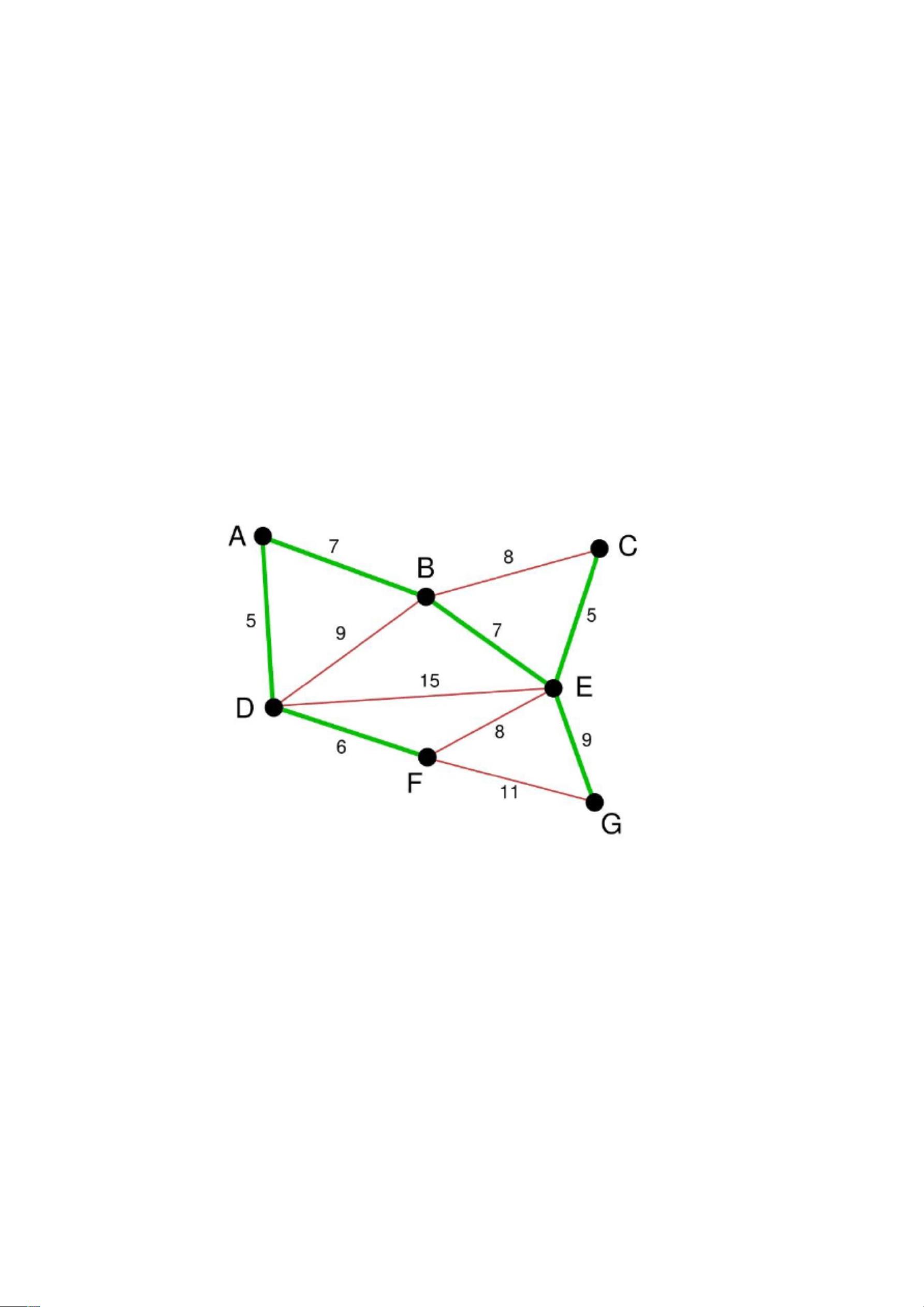
【克鲁斯卡尔算法（Kruskal’s Algorithm）】是一种用于寻找给定加权无向图的最小生成树的贪心算法。最小生成树是指在无向图中找到一棵包括所有顶点，且边的权重之和尽可能小的树。算法的基本思想是按边的权重递增顺序依次考虑每条边，并确保在添加新边时不形成环路。 ### 算法定义 1. **初始化**：创建一个包含所有顶点但无边的子图，即一个包含n棵独立树的森林。 2. **边的选择**：遍历边集E，按权重从小到大排序。 3. **边的添加**：检查每条边的两个端点是否已经在同一个连通分量（树）中。如果不在，这条边会被添加到子图中，将两个分量合并为一棵更大的树。如果已经在同一个分量中，这条边将被忽略，因为它会导致环路的形成。 4. **重复步骤3**，直到森林中只剩下一棵树，即子图包含n-1条边。 ### 举例描述 以一个简单的图为例，假设图中有若干顶点和边。算法开始时，首先对所有边按权重进行排序。接着，选择权值最小的边，如果这条边连接的是不同树上的顶点，就将其添加到最小生成树中。如果发现添加边会导致环路，就选择下一条最小的边尝试。这一过程持续进行，直到所有顶点都在同一棵树下，即形成了一个最小生成树。 ### 代码实现 - **伪代码**： ```markdown MST-KRUSKAL(G, w) 1. 初始化一个空的边集合T 2. 将所有边按权重升序排序 3. 对于每条边(e)按顺序： a. 如果e的两个顶点不在T中相同的连通分量中，将e添加到T 4. 返回T ``` - **C语言实现**： ```c // 省略部分代码... for(k=1;k<=num;k++){ printf("请输入第%d条边的两个顶点号和它的权重:\n",k); scanf("%d%d%d",&v1,&v2,&temp); G[v1][v2]=G[v2][v1]=temp; } // 省略部分代码... while(exsit==0){ for(i=1;i<=num;i++){ for(j=i+1;j<=num;j++){ if(G[i][j]<min&&FindCircle(i,j,num,0)==0){ min=G[i][j]; t=i; exsit++; } } } if(exsit==1){ printf("边 %d-%d(权值：%d) 被选入最小生成树\n",t,path[record][0],path[record][1]); record++; exsit--; }else{ printf("没有边可选\n"); } } // 省略部分代码... ``` - **MATLAB代码实现**： MATLAB代码通常使用矩阵或结构体来表示图，然后通过循环和条件判断来实现算法逻辑，这里省略具体实现，因为MATLAB代码通常比C等语言更复杂，涉及图形操作和数据结构的处理。 - **Pascal代码实现**： Pascal代码同样会涉及到数据结构的定义和遍历，但这里也省略具体实现，因为与C语言类似，它会涉及到边和顶点的数据结构定义以及遍历算法的实现。 ### 总结 克鲁斯卡尔算法是解决最小生成树问题的有效方法之一，其核心在于贪心策略，即每次都选择当前剩余边中最优的一条。由于算法依赖于边的排序，所以实际运行时间取决于排序的效率。虽然Kruskal算法在处理边较多且边权重差异较大的情况时效果较好，但在边权重接近或者图高度连通时，Prim算法可能是一个更好的选择，因为它更侧重于以顶点为中心扩展最小生成树。