信号处理:信号本质的大飞跃.docx
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
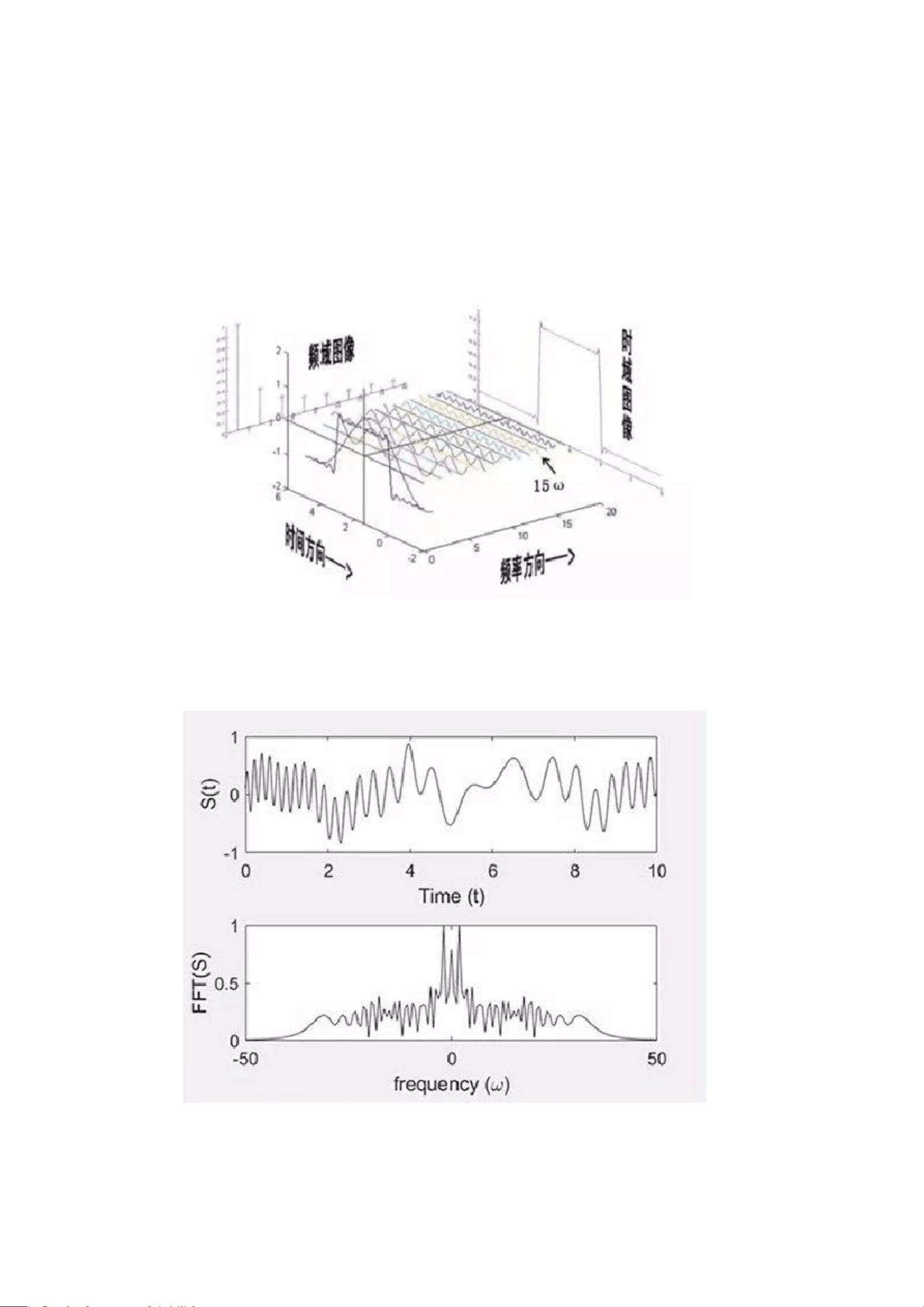
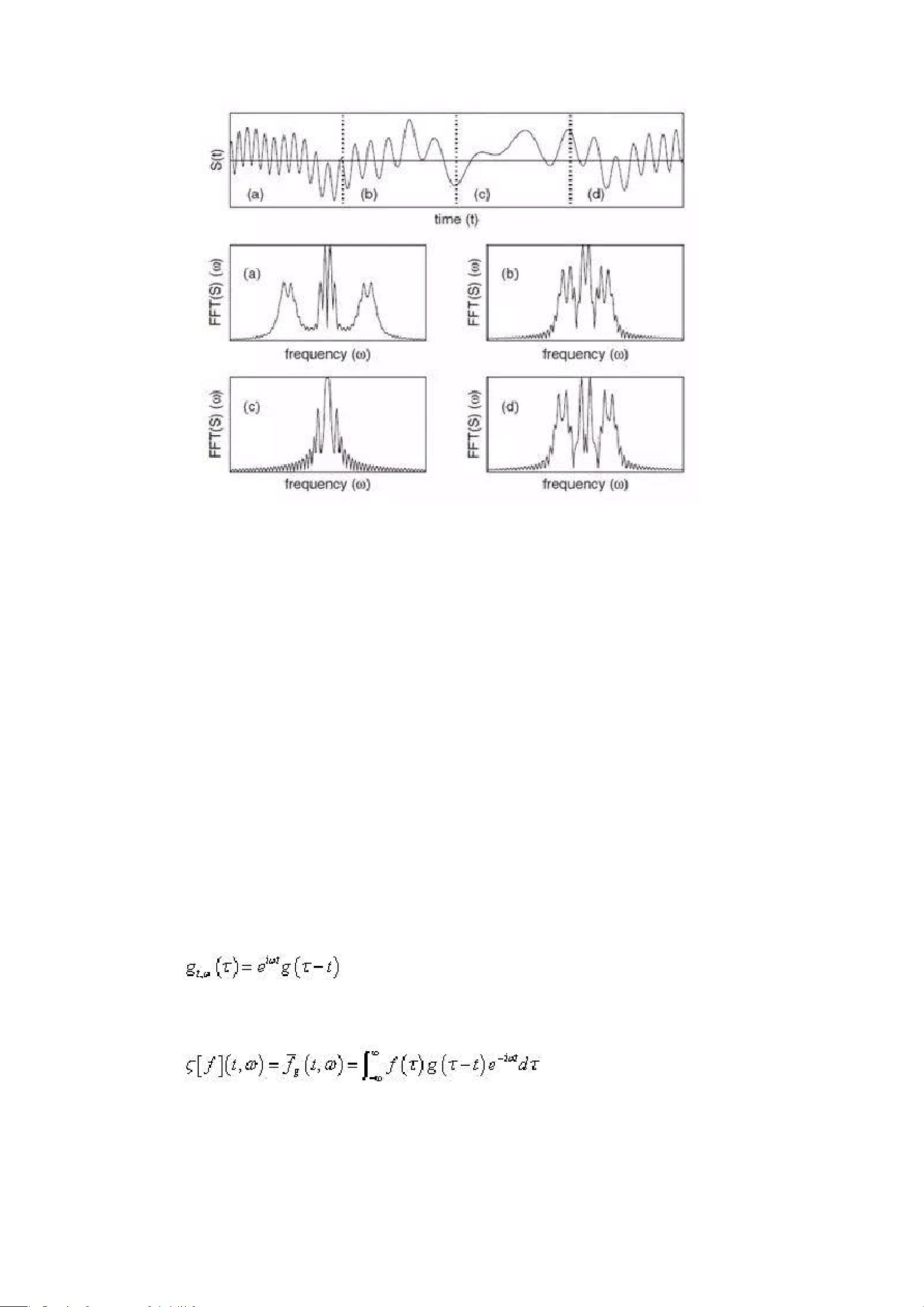
【信号处理:从时域到频域的跨越】 信号处理是信息技术领域的重要组成部分,它涉及到对信号的分析、转换和优化。从最初的时域统计分析到傅里叶变换的频域分析,这是一个认识信号本质的重大进步。傅里叶变换通过将信号从时域转化为频域,揭示了信号的频率成分,但同时也暴露了一些局限性。 傅里叶变换是全局性的,无法提供频率随时间变化的信息。例如,对于一个初始频率高、中间频率低的信号s(t),傅里叶变换能显示所有频率成分,却无法指示高频和低频在何时出现。这促使了人们对时频分析的需求,期望能够同时获取信号的时域和频域信息。 为了解决这个问题,短时傅里叶变换(STFT)应运而生。STFT通过对信号进行分段,并对每一小段应用快速傅里叶变换(FFT),从而得到信号的时频分布。形象地说,就像将时域分解成多个小段,每个小段近似为平稳信号,然后分别进行频域分析。这样,我们就能得知信号在不同时间点的频率信息。Gabor变换是STFT的一种特殊情况,选择高斯窗函数作为窗函数,是因为高斯函数的傅里叶变换仍然是高斯函数,这使得频率域的局部化得以实现,同时满足了Heisenberg测不准原理的最优条件。 然而,Gabor变换的时频窗口大小和形状固定,无法根据信号频率的变化进行调整,导致了对突变信号和非平稳信号分析的不足。为了克服这一局限,小波变换被提出。小波变换的核心是引入可变长度和形状的小波基函数,如db系列和coif系列小波,它们能自适应地适应信号的频率变化。小波基函数不是固定的,而是可以平移、缩放,这赋予了小波变换强大的时频局部化能力。 小波变换通过定义连续小波变换(CWT),使用形如ψa,b(t)的窗函数,其中a控制缩放,b控制平移,可以实现对不同频率信号的自适应分析。与傅里叶变换相比,小波变换的基函数是有限长且会衰减的,如Haar小波,它在定位信号方面优于傅里叶变换,但在频域解析上可能不如傅里叶变换精确,因为它类似于sinc函数。 总结来说,信号处理经历了从时域统计、傅里叶变换、短时傅里叶变换到小波变换的发展,不断追求对信号时频信息的更精细理解。这些方法各有优劣,适用于不同的信号类型和分析需求,为现代通信、图像处理、数据压缩等多个领域提供了强大的理论支持。


剩余15页未读,继续阅读

- 粉丝: 1w+
- 资源: 6万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功