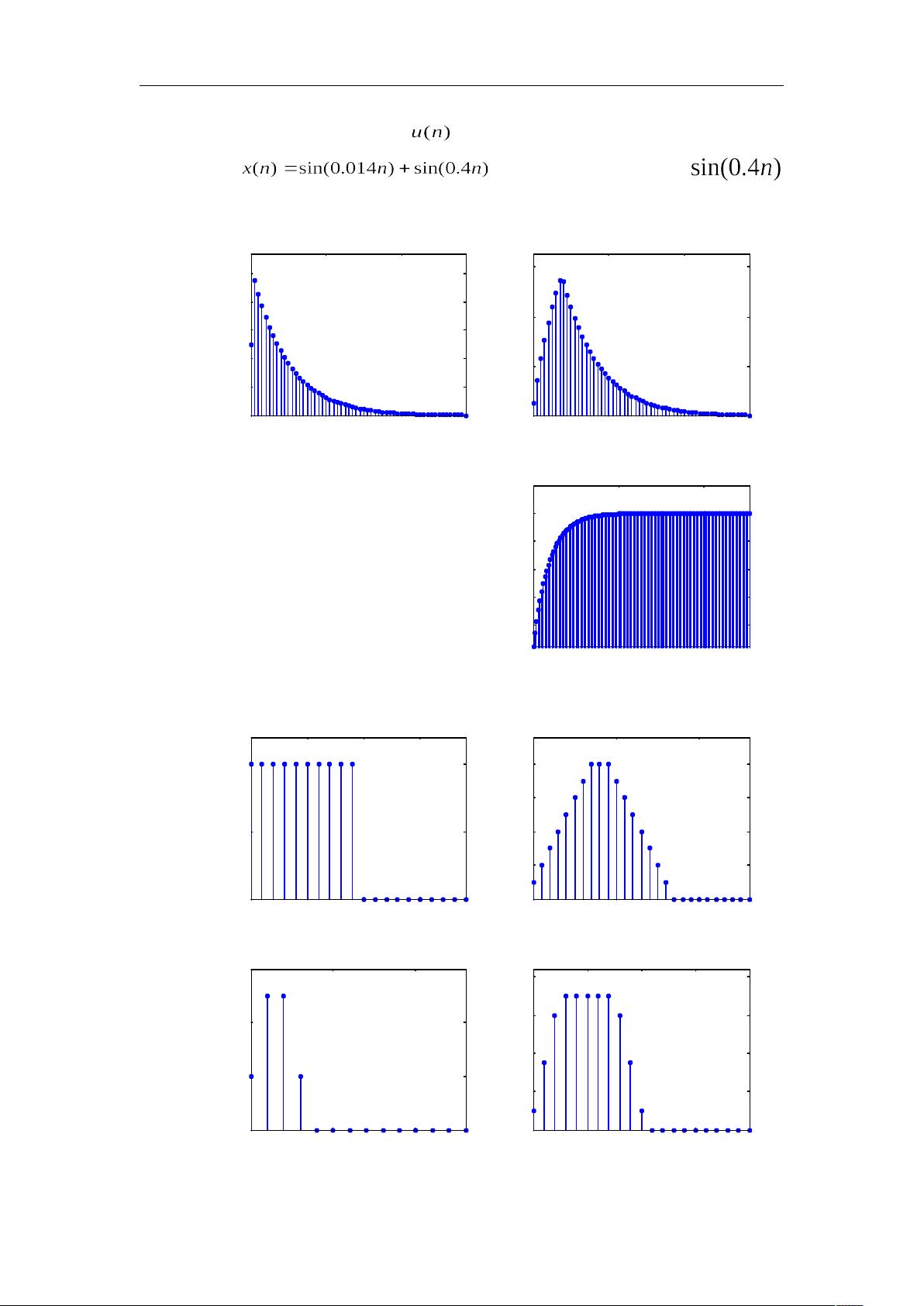
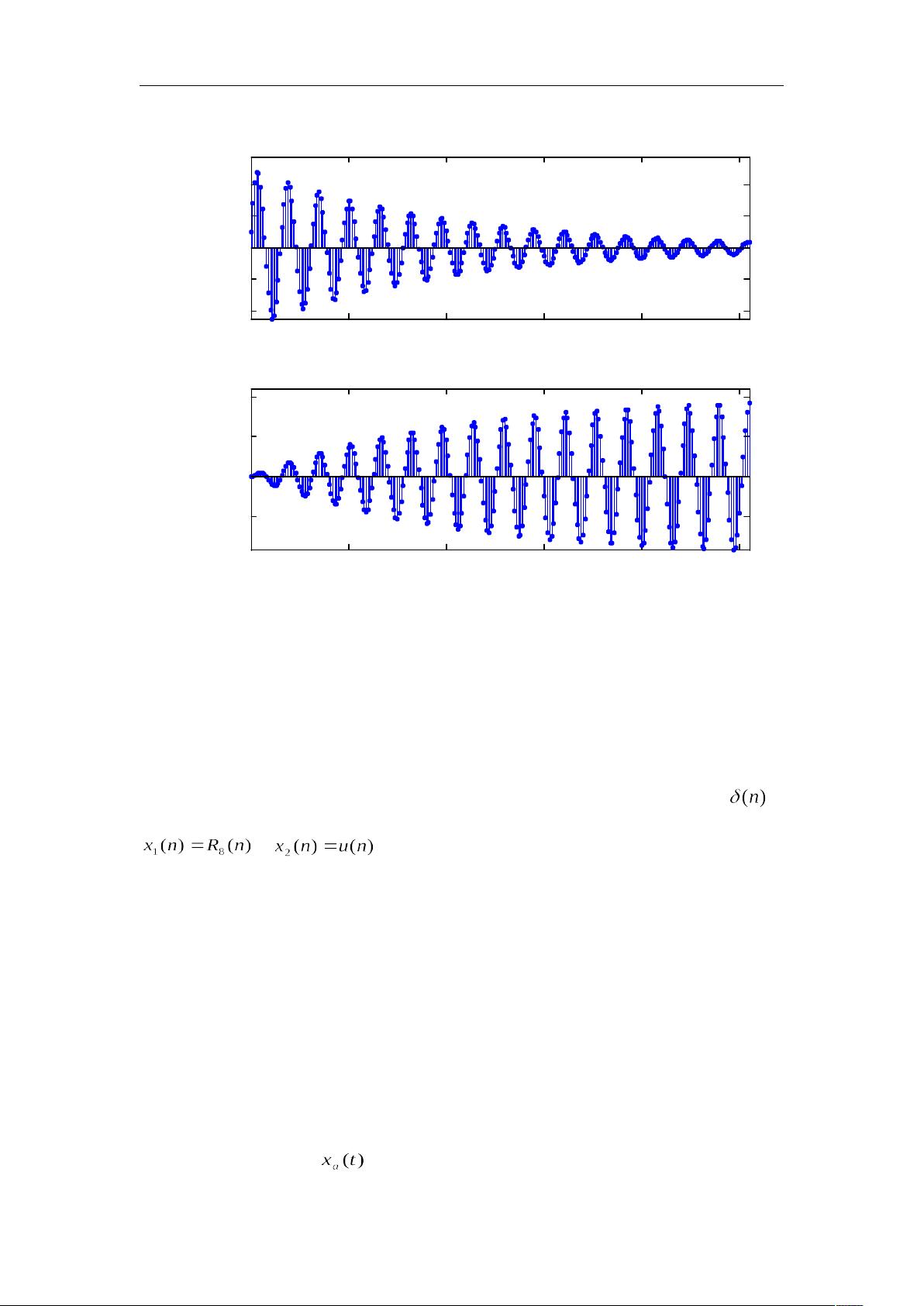
数字信号处理（第四版）上机实验答案 西电版

数字信号处理（第四版）上机实验答案 西电版 数字信号处理是一门理论和实际密切结合的课程，为深入掌握课程内容，最好在学习理论的同时，做习题和上机实验。上机实验不仅可以帮助读者深入的理解和消化基本理论，而且能锻炼初学者的独立解决问题的能力。本章在第二版的基础上编写了六个实验，前五个实验属基础理论实验，第六个属应用综合实验。 实验一：系统响应及系统稳定性 实验目的： 1. 掌握求系统响应的方法。 2. 掌握时域离散系统的时域特性。 3. 分析、观察及检验系统的稳定性。 实验原理与方法： 在时域中，描写系统特性的方法是差分方程和单位脉冲响应，在频域可以用系统函数描述系统特性。已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应，本实验仅在时域求解。在计算机上适合用递推法求差分方程的解，最简单的方法是采用 MATLAB 语言的工具箱函数 filter 函数。也可以用 MATLAB 语言的工具箱函数 conv 函数计算输入信号和系统的单位脉冲响应的线性卷积，求出系统的响应。 系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。重点分析实验系统的稳定性，包括观察系统的暂态响应和稳定响应。系统的稳定性是指对任意有界的输入信号，系统都能得到有界的系统响应。或者系统的单位脉冲响应满足绝对可和的条件。系统的稳定性由其差分方程的系数决定。 实际中检查系统是否稳定，不可能检查系统对所有有界的输入信号，输出是否都是有界输出，或者检查系统的单位脉冲响应满足绝对可和的条件。可行的方法是在系统的输入端加入单位阶跃序列，如果系统的输出趋近一个常数（包括零），就可以断定系统是稳定的。 实验内容及步骤： （1）编制程序，包括产生输入信号、单位脉冲响应序列的子程序，用 filter 函数或 conv 函数求解系统输出响应的主程序。程序中要有绘制信号波形的功能。 （2）给定一个低通滤波器的差分方程为 用线性卷积法分别求系统对输入信号的响应序列，并画出其波形。 （3）给定系统的单位脉冲响应为 用线性卷积法分别求系统对输入信号的响应序列，并画出其波形。 （4）给定一谐振器的差分方程为 令谐振器的谐振频率为 0.4rad。 a) 用实验方法检查系统是否稳定。输入信号为时，画出系统输出波形。 b) 给定输入信号为 求出系统的输出响应，并画出其波形。 思考题： （1）如果输入信号为无限长序列，系统的单位脉冲响应是有限长序列，可否用线性卷积法求系统的响应？如何求？ （2）如果信号经过低通滤波器，把信号的高频分量滤掉，时域信号会有何变化，用前面第一个实验结果进行分析说明。 实验报告要求： （1）简述在时域求系统响应的方法。 （2）简述通过实验判断系统稳定性的方法。分析上面第三个实验的稳定输出的波形。 （3）对各实验所得结果进行简单分析和解释。 （4）简要回答思考题。 （5）打印程序清单和要求的各信号波形。 实验程序清单： %实验 1：系统响应及系统稳定性 close all; clear all %====== 内容 1：调用 filter 解差分方程，由系统对 u(n)的响应判断稳定性====== A=[1,-0.9]; B=[0.05,0.05]; %系统差分方程系数向量 B 和 A x1n=[1 1 1 1 1 1 1 1 zeros(1,50)]; %产生信号 x1(n)=R8(n) x2n=ones(1,128); %产生信号 x2(n)=u(n) hn=impz(B,A,58); %求系统单位脉冲响应 h(n) subplot(2,2,1); y='h(n)'; tstem(hn,y) ...