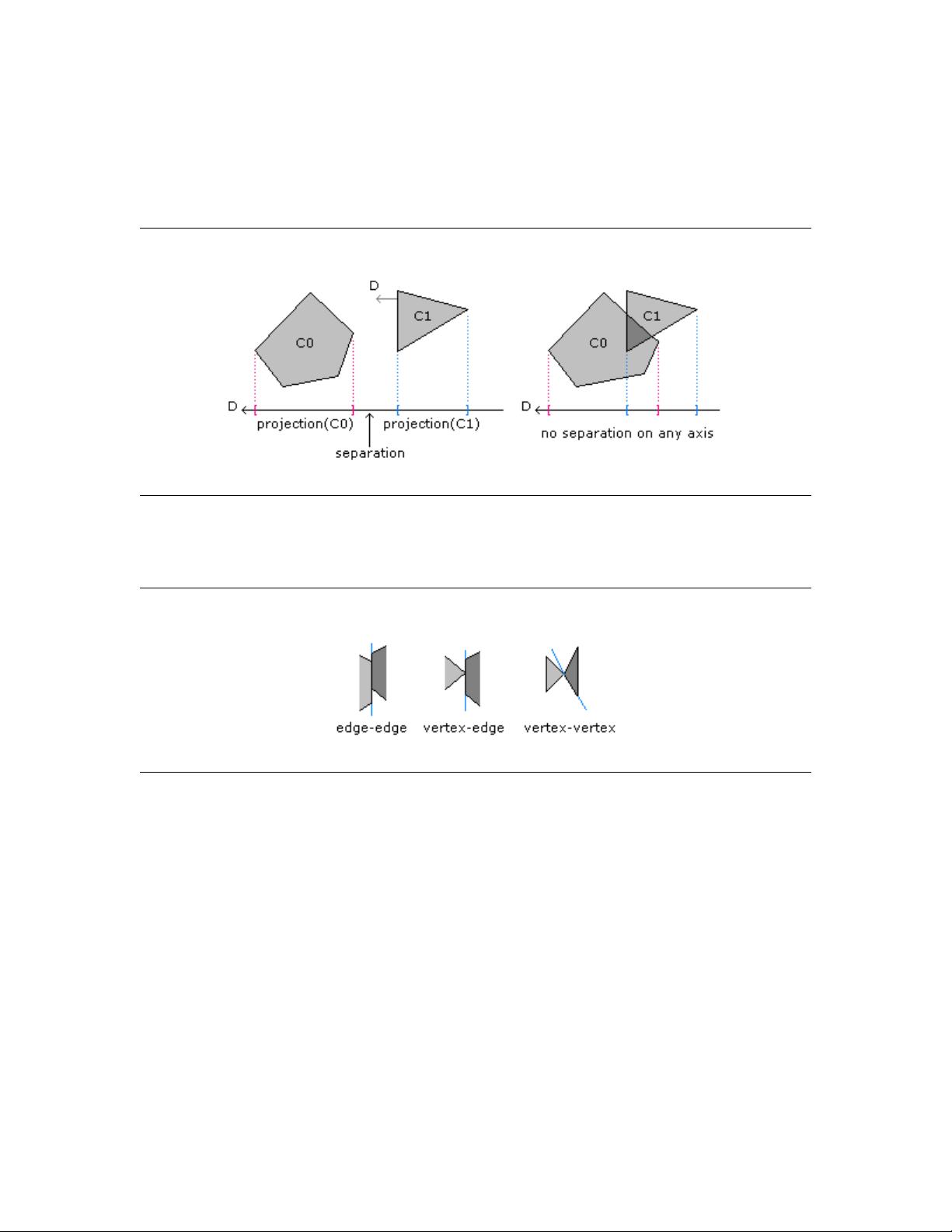
### 分离轴方法详解 #### 一、引言 本文档详细介绍了分离轴方法,这是一种用于确定两个静态凸对象是否相交的有效手段。此外,该方法还可以扩展到处理移动的凸对象,对于预测这些对象之间的碰撞以及计算它们首次接触的时间非常有用。本文档目前主要关注的是测试交集几何查询问题,即仅仅判断两个对象之间是否存在交集或在移动时是否会相交。而找到交集的具体集合被称为寻找交集几何查询,通常比测试交集查询更难实现。测试查询的信息可以帮助确定寻找查询必须构建的接触集。本文将详细阐述如何利用测试查询的信息。 #### 二、通过投影到一条直线上的分离 两个凸对象不相交的测试方法可以简单地表述为:如果存在一条直线,使得这两个对象在此直线上的投影区间不相交,则这两个对象不相交。这样的直线被称为分离线或者更常见的称为分离轴。由于直线的平移仍然是分离线,因此可以考虑包含原点且方向单位向量为 \(D\) 的直线。给定一个包含原点且方向为单位长度 \(D\) 的直线,凸集 \(C\) 在这条直线上的投影区间是 \[I = [\lambda_{\text{min}}(D), \lambda_{\text{max}}(D)] = [\min\{D \cdot X : X \in C\}, \max\{D \cdot X : X \in C\}]\] 其中,\(D \cdot X\) 表示向量 \(D\) 与点 \(X\) 的点积。 若两个紧凑的凸集 \(C_0\) 和 \(C_1\) 满足以下条件之一,则认为它们是分离的: - \(\lambda_{\text{min}}^{(0)}(D) > \lambda_{\text{max}}^{(1)}(D)\) - \(\lambda_{\text{max}}^{(0)}(D) < \lambda_{\text{min}}^{(1)}(D)\) 这里,\(\lambda_{\text{min}}^{(0)}(D)\) 和 \(\lambda_{\text{max}}^{(0)}(D)\) 分别表示 \(C_0\) 在方向 \(D\) 上的投影区间的最小值和最大值;\(\lambda_{\text{min}}^{(1)}(D)\) 和 \(\lambda_{\text{max}}^{(1)}(D)\) 分别表示 \(C_1\) 在方向 \(D\) 上的投影区间的最小值和最大值。 #### 三、二维空间中的凸多边形分离 在二维空间中,如果两个凸多边形 \(P_0\) 和 \(P_1\) 不相交,则存在至少一个方向 \(D\),使得 \(P_0\) 和 \(P_1\) 在方向 \(D\) 上的投影区间不相交。为了找到这样的方向,需要考虑所有可能的边缘方向。具体来说,每个多边形都有多个边,每条边定义了一个方向。对于两个多边形 \(P_0\) 和 \(P_1\),需要检查以下几种情况: - \(P_0\) 的每条边所定义的方向。 - \(P_1\) 的每条边所定义的方向。 - 如果两个多边形共享一条边界,则还需检查这条边的法线方向。 通过逐一检查这些方向,可以确定是否存在分离轴,从而判断两个凸多边形是否相交。 #### 四、三维空间中的凸多面体分离 在三维空间中,对于两个凸多面体 \(P_0\) 和 \(P_1\) 的分离轴检测更加复杂。除了考虑边缘定义的方向之外,还需要考虑由多面体表面定义的法线方向。具体步骤包括: - 检查 \(P_0\) 的每个面的法线方向。 - 检查 \(P_1\) 的每个面的法线方向。 - 检查由两个多面体共享边所定义的方向。 - 检查由两个相邻面的边缘构成的“边缘对”所定义的方向。 通过这种方式,可以找到潜在的分离轴,从而判断两个凸多面体是否相交。 #### 五、三维空间中的凸多边形分离 在三维空间中处理二维凸多边形时,通常将这些多边形视为平面内的对象。此时,分离轴方法类似于二维空间中的处理方式,但需要注意的是,除了考虑二维空间中的边方向外,还需要考虑多边形所在平面的法线方向。这意味着不仅要检查每个多边形边的方向,还要检查多边形所在平面的法线方向,以确保在三维空间中的分离轴检测准确无误。 #### 六、移动的凸对象分离 当考虑移动的凸对象时,需要将时间和速度等因素考虑进来。在这种情况下,可以通过分析对象的运动轨迹来确定它们之间是否存在潜在的分离轴。具体来说,可以计算在不同的时间点上两个移动对象的位置,并在这些位置上应用分离轴方法来确定它们是否会在某个时刻相交。 #### 七、移动凸对象的接触集 接触集是指两个移动的凸对象在相交时的接触点集合。为了确定接触集,首先需要通过测试查询判断两个对象是否会在未来的某个时间点相交。如果会相交,那么接下来的任务是找出它们首次接触的时间点,并在这个时间点上确定接触点的位置。 #### 八、示例:两个二维移动三角形 考虑两个在二维空间中移动的三角形。根据它们的初始位置和速度向量来计算它们在不同时间点的位置。然后,对每个时间点应用分离轴方法来判断它们是否相交。如果存在相交的情况,还需要进一步分析它们首次接触的时间点,并确定接触点的位置。 #### 九、示例:两个三维移动三角形 对于三维空间中的两个移动三角形,处理方式与二维情况类似。需要考虑三角形在三维空间中的位置和速度,并对每个时间点进行分离轴检测。如果两个三角形在某个时间点相交,则需要确定首次接触的时间点和接触点的位置。 通过以上内容可以看出,分离轴方法是一种非常强大的工具,不仅可以用来判断静态凸对象是否相交,还可以扩展到处理移动的凸对象,从而解决一系列复杂的问题。




剩余20页未读,继续阅读

- 粉丝: 101
- 资源: 5
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 基于mpc模型预测轨迹跟踪控制,总共包含两套仿真,一套是不加入四轮侧偏角软约束,一套是加入四轮侧偏角的软约束控制,通过carsim与simulink联合仿真发现加入侧偏角软约束在进行轨迹跟踪时,能够通
- 字节跳动人工智能模型DeepSeek:语言理解生成、多模态技术及其广泛应用与未来展望
- 排序算法研究: 快速排序(Quick Sort)原理及其Python实现解析
- java.抽象类与接口(解决方案).md
- 第1章 开始启程-你的第一行Android代码.pdf
- 深度学习中卷积神经网络(CNN)的基本原理及其应用
- 离网型 三相光伏 发电 主电路设计 控制电路设计 以及参数设计 Matlab SIMLINK 仿真 离网 并网 1.主电路设计:光伏boost模块 MPPT 储能双向DC-DC 逆变DC
- FileNotFoundException如何解决.md
- 使用Python正则表达式校验中国大陆手机号格式
- 第2'章 Kotlin语言.pdf
- Java毕业设计基于springboot的物业管理系统源码+数据库(高分项目)
- 第2章 先从看得到的入手,探究活动.pdf
- 第3章 软件也要拼脸蛋,UI开发的点点滴滴.pdf
- 基于javaweb的社区物资交易互助平台.zip
- 文章复现:拉盖尔高斯光束入射石英基底石墨烯涂层的透射光强分布特性研究
- DigitalPlat FreeDomain – Your Free Domain Awaits!


 信息提交成功
信息提交成功