用C语言求解N阶线性矩阵方程Ax=b的简单解法

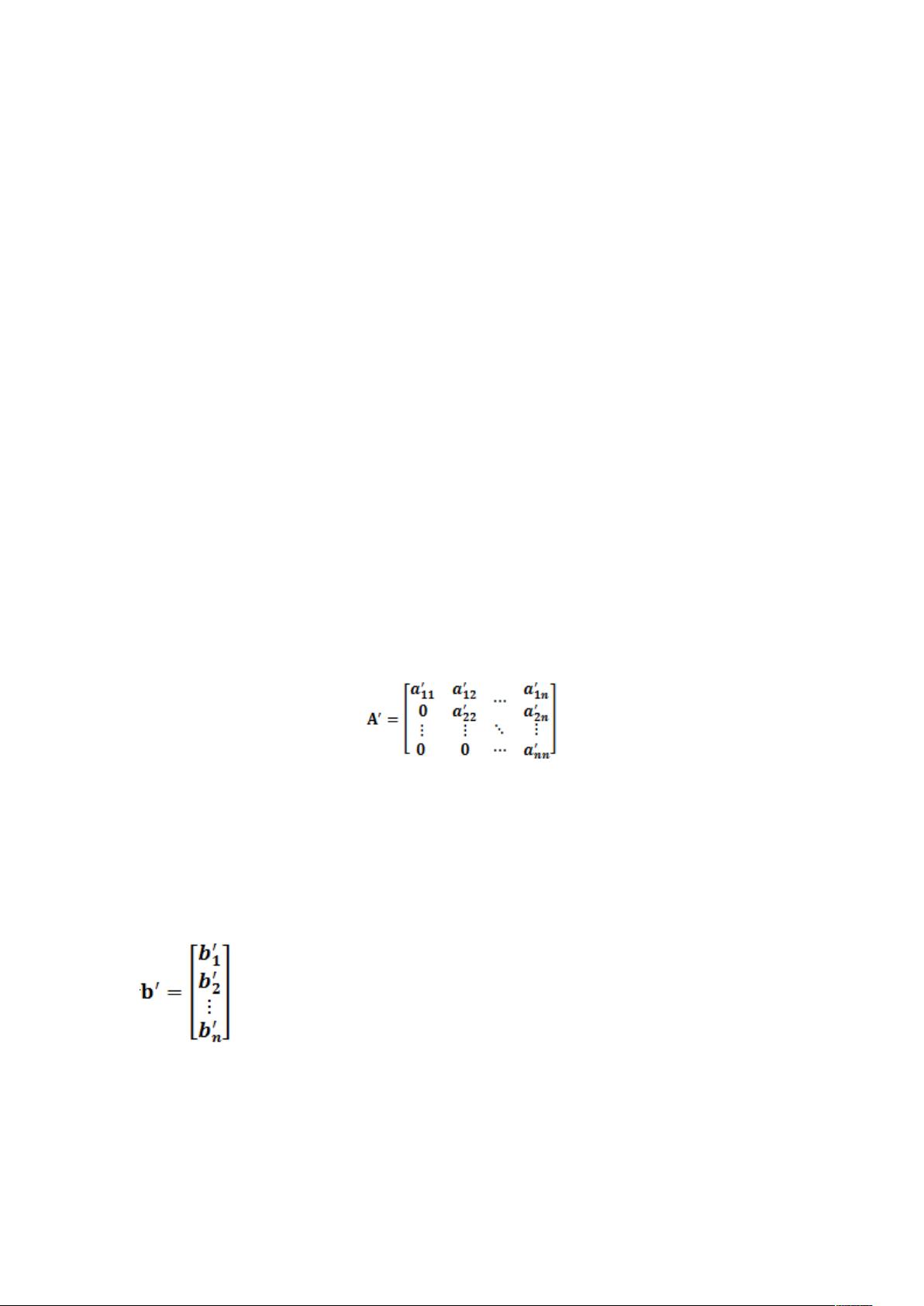
1. #include<stdio.h> 2. #include<stdlib.h> 3. #include<math.h> 4. #define dim 10 //定义最大的维数10，为防止计算值溢出 5. double a[dim+1][dim+1],b[dim+1],x[dim+1]; //定义双精度数组 6. double temp; 7. double getarray(int n); //定义输入矩阵元素的函数 8. double showarray(int n); //定义输出化简系数矩阵过程的函数 9. int n,i,j,k,p,q; 10. double main() 11. { 12. 13. printf("请输入系数矩阵的阶数n(n<10):"); 14. scanf("%d",&n); 15. /*判断矩阵阶数是否超过界定值*/ 16. if(n>dim) 17. { 18. printf("错误：元数超过初设定的值%d，请重启程序重新输入\n",dim); 19. exit(0); 20. } 21. 22. /*输入系数矩阵和常数矩阵（即增广矩阵）的元素*/ 23. getarray(n); 24. 25. /*使对角线上的主元素不为0*/ 26. for(j=1;j<=n-1;j++) 27. { 28. if(a[j][j]==0) 29. for(i=j+1;i<=n;i++) 30. { 31. if(a[i][j]!=0) 32. { 33. /*交换增广矩阵的第i行与第j行的所有元素*/ 在C语言中，解决N阶线性矩阵方程Ax=b的问题通常采用高斯消元法。这是一种数值计算方法，用于将系数矩阵A转换为上三角矩阵，从而方便地求解未知向量x。以下是实现这一过程的关键步骤和知识点： 1. **定义变量和数据结构**： 在代码中，`#define dim 10`定义了最大维数10，避免计算溢出。`double a[dim+1][dim+1]`, `b[dim+1]`, `x[dim+1]`分别用于存储系数矩阵A、常数向量b和未知向量x。`temp`作为临时变量用于交换或计算。 2. **输入矩阵元素**： `getarray(int n)`函数用于从用户处获取n阶系数矩阵A和常数向量b的元素。 3. **检查矩阵阶数**： 程序通过`scanf`读取用户输入的阶数n，并在`if(n>dim)`条件中判断是否超过预设的最大维数。如果超过，提示用户重启程序。 4. **高斯消元法**： - **主元选择**：在每一步迭代中，找到对角线上下标为j的元素ajj，若ajj=0，则需要从j列后面的元素中找到第一个非零元素，通过交换行使得ajj非零。 - **行变换**：对于第j列，通过第三类初等行变换交换行，使得ajj成为该列的最大值。然后，通过第二类初等行变换（除以ajj）将对角线上的其他元素变为0。 5. **计算过程**： 一旦得到上三角矩阵，通过回代法（back-substitution）求解未知向量x。从最后一行开始，利用矩阵的上三角形式，依次解出xn, xn-1, ..., x1。 6. **编程实现**： 主函数`main()`中，包含了输入、判断和计算的主要流程。`showarray(int n)`函数可能用于展示化简过程中系数矩阵的变化，方便调试和理解算法。 7. **最小二乘拟合**： 尽管题目标签提到“最小二乘拟合”，但给出的代码并未涉及此概念。最小二乘拟合是当线性方程组无解或解不唯一时，寻找最佳近似解的方法，通过最小化残差平方和来实现。在实际应用中，如果矩阵A的秩小于n，可以使用最小二乘法找到最接近的解。 用C语言求解N阶线性矩阵方程Ax=b主要涉及高斯消元法和回代法，通过行变换将系数矩阵化为上三角形，再通过回代求解未知向量。如果矩阵的阶数超过设定值或者系数矩阵行列式为0，则需要处理特殊情况进行调整。而最小二乘拟合则是在无法直接求解时，寻找误差最小的解的一种策略。