没有合适的资源？快使用搜索试试~ 我知道了~

文库首页课程资源专业指导支持向量机通俗导论

支持向量机通俗导论

支持向量机

需积分: 13 1 下载量 131 浏览量 2018-10-15 18:37:44 上传评论收藏 2.06MB PDF 举报

温馨提示

试读

52页

支持向量机，因其英文名为support vector machine，故一般简称SVM，通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

资源推荐

资源详情

资源评论

支持向量机通俗导论

理解 aoJ 的三层境界

作者： CmHv

致谢： THmbFB/、白石、C2``vG2/

出处：结构之法算法之道 #HQ;

目录 k

R 第一层：了解 aoJ 9

RXR 分类标准的起源：GQ;BbiB+ 回归 XXXXXXXXXXXXXXXXXXXXXXXX 9

RXk 线性分类的一个例子 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXX 8

RXj 函数间隔 6mM+iBQMH K`;BM 与几何间隔 :2QK2i`B+H K`;BM XXXXXXX 3

RX9 最大间隔分类器 JtBKmK J`;BM *HbbB}2` 的定义 XXXXXXXXXXXX N

k 第二层：深入 aoJ Rk

kXR 从线性可分到线性不可分 XXXXXXXXXXXXXXXXXXXXXXXXXXX Rk

kXRXR 从原始问题到对偶问题的求解 XXXXXXXXXXXXXXXXXXXXX Rk

kXRXk EXEXhX 条件 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXX Rj

kXRXj 对偶问题求解的 j 个步骤 XXXXXXXXXXXXXXXXXXXXXXX R9

kXRX9 线性不可分的情况 XXXXXXXXXXXXXXXXXXXXXXXXXXX Re

kXk 核函数：E2`M2H XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX R3

kXkXR 特征空间的隐式映射：核函数 XXXXXXXXXXXXXXXXXXXXX R3

kXkXk 核函数：如何处理非线性数据 XXXXXXXXXXXXXXXXXXXXX RN

kXkXj 几个核函数 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX kk

kXkX9 核函数的本质 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXX kj

kXj 使用松弛变量处理 QmiHB2`b 方法 XXXXXXXXXXXXXXXXXXXXXXXX k9

j 证明 aoJ kN

jXR 线性学习器 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX kN

jXRXR 感知器算法 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX kN

jXk 非线性学习器 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX jR

jXkXR J2`+2` 定理 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX jR

jXj 损失函数 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX jk

jX9 最小二乘法 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX j9

jX9XR 什么是最小二乘法？ XXXXXXXXXXXXXXXXXXXXXXXXXX j9

jX9Xk 最小二乘法的解法 XXXXXXXXXXXXXXXXXXXXXXXXXXX j8

jX8 aJP 算法 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX jd

jX8XR aJP 算法的推导 XXXXXXXXXXXXXXXXXXXXXXXXXXXX jd

jX8Xk aJP 算法的步骤 XXXXXXXXXXXXXXXXXXXXXXXXXXXX 9k

jX8Xj aJP 算法的实现 XXXXXXXXXXXXXXXXXXXXXXXXXXXX 99

jXe aoJ 的应用 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX 98

jXeXR 文本分类 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX 98

目录 j

前言

动笔写这个支持向量机 UamTTQ`i o2+iQ` J+?BM2

V 是费了不少劲和困难的，原

因很简单，一者这个东西本身就并不好懂，要深入学习和研究下去需花费不少时间和精

力，二者这个东西也不好讲清楚，尽管网上已经有朋友写得不错了 U见文末参考链接V，

但在描述数学公式的时候还是显得不够。得益于同学白石的数学证明，我还是想尝试写

一下，希望本文在兼顾通俗易懂的基础上，真真正正能足以成为一篇完整概括和介绍支

持向量机的导论性的文章。

本文在写的过程中，参考了不少资料，包括《支持向量机导论》、《统计学习方法》

及网友 THmbFB/ 的支持向量机系列等等，于此，还是一篇学习笔记，只是加入了自己的

理解和总结，有任何不妥之处，还望海涵。全文宏观上整体认识支持向量机的概念和用

处，微观上深究部分定理的来龙去脉，证明及原理细节，力保逻辑清晰  通俗易懂。

同时，阅读本文时建议大家尽量使用 +?`QK2 等浏览器，如此公式才能更好的显示，

再者，阅读时可拿张纸和笔出来，把本文所有定理X 公式都亲自推导一遍或者直接打印

下来（可直接打印网页版或本文文末附的 S.6，享受随时随地思考、演算的极致快感），

在文稿上演算。

PEG，还是那句原话，有任何问题，欢迎任何人随时不吝指正  赐教，感谢。

?iiT,ff2MXrBFBT2/BXQ`;frBFBfamTTQ`inp2+iQ`nK+?BM2

R 第一层：了解 aoJ 9

R 第一层：了解 aoJ

支

持向量机，因其英文名为 amTTQ`i o2+iQ` J+?BM2，故一般简称 aoJ，通俗

来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线

性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

RXR 分类标准的起源：GQ;BbiB+ 回归

理解 aoJ，咱们必须先弄清楚一个概念：线性分类器。

给定一些数据点，它们分别属于两个不同的类，现在要找到一个线性分类器把这些

数据分成两类。如果用 x 表示数据点，用 y 表示类别（y 可以取 1 或者 −1，分别代表

两个不同的类），一个线性分类器的学习目标便是要在 n 维的数据空间中找到一个超平

面（?vT2` THM2），这个超平面的方程可以表示为（w

中的 T 代表转置）：

x + b =0 URXRV

可能有读者对类别取 1 或 −1 有疑问，事实上，这个 1 或 −1 的分类标准起源于

GQ;BbiB+ 回归

。

定义 R UGQ;BbiB+ 回归V GQ;BbiB+ 回归目的是从特征学习出一个 yfR 分类模型，而这个

模型是将特征的线性组合作为自变量，由于自变量的取值范围是负无穷到正无穷，因

此，使用 GQ;BbiB+ 函数（或称作 bB;KQB/ 函数）将自变量映射到 (0, 1) 上，映射后的值

被认为是属于 y =1的概率。

假设函数,

(x)=g(θ

x)=

1+e

−θ

URXkV

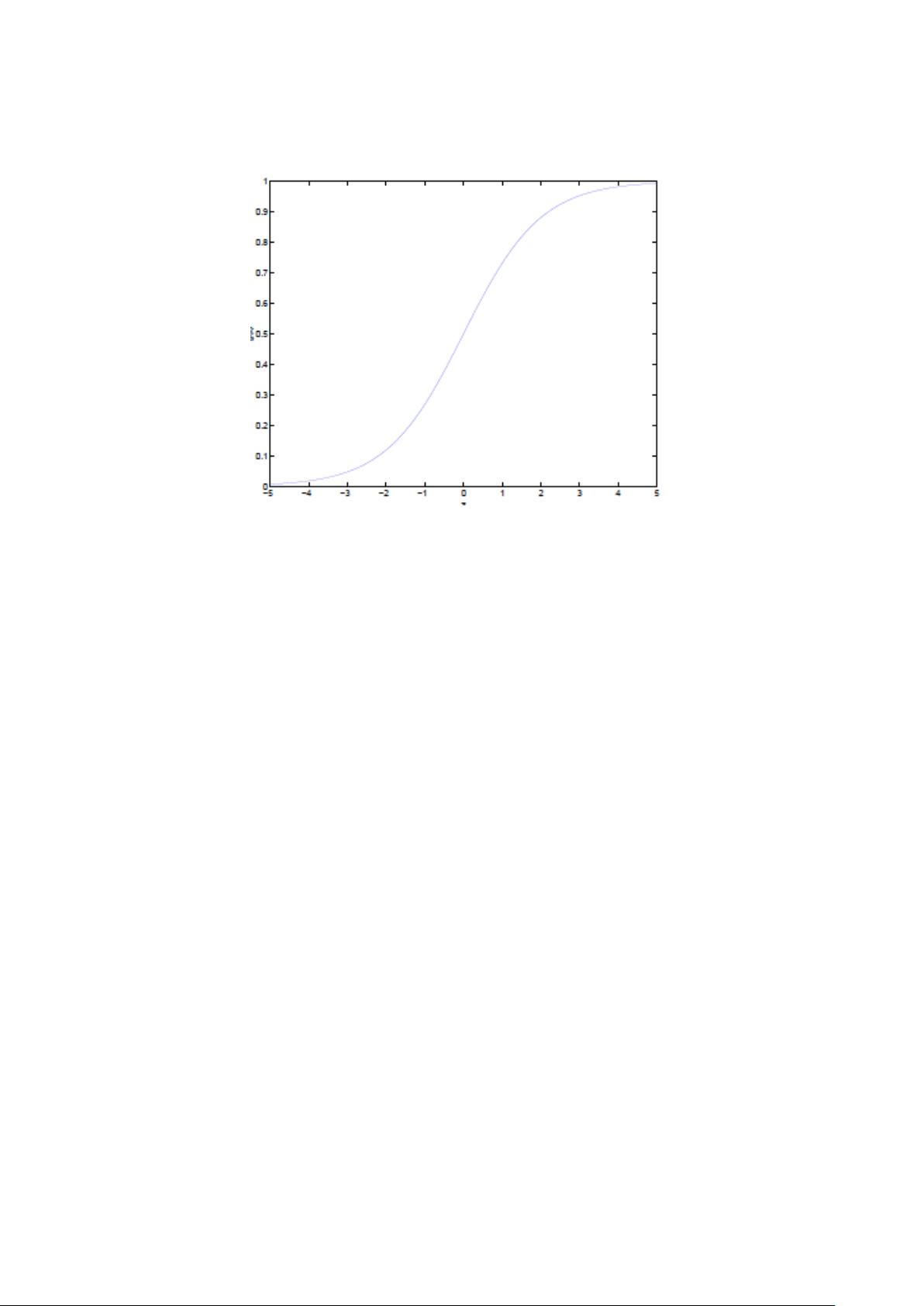
其中，x 是 n 维特征向量，函数 g 就是 GQ;BbiB+ 函数。而 g(z)=

1+e

−z

的图像如

图R，将无穷映射到了 (0, 1)。

而假设函数就是属于 y =1的概率：

P (y =1|x; θ)=h

(x) URXjV

P (y =0|x; θ)=1−h

(x) URX9V

从而，当我们要判别一个新来的特征属于哪个类时，只需求 h

(x) 即可，若 h

(x)

大于 yX8 就是 y =1的类，反之属于 y =0类。

?iiT,ff2MXrBFBT2/BXQ`;frBFBfGQ;BbiB+n`2;`2bbBQM

R 第一层：了解 aoJ 8

图 R, GQ;BbiB+ 函数图像

此外，h

(x) 只和 θ

x 有关，θ

x>0，那么 h

(x) > 0.5，而 g(z) 只是用来映射，

真实的类别决定权还是在于 θ

x。再者，当 θ

x ≫ 0 时，h

(x)=1，反之 h

(x)=0。如

果我们只从 θ

x 出发，希望模型达到的目标就是让训练数据中 y =1的特征 θ

x ≫ 0，

而 y =0的特征 θ

x ≪ 0。GQ;BbiB+ 回归就是要学习得到 θ，使得正例的特征远大于 y，

负例的特征远小于 y，而且要在全部训练实例上达到这个目标。

接下来，尝试把 GQ;BbiB+ 回归做个变形。首先，将使用的结果标签 y =0和 y =1

替换为 y = −1，y =1，然后将 θ

x = θ

+ θ

+ ···+ θ

=1)中的 θ

替换

为 b，最后将后面的 θ

+ θ

+ ···+ θ

替换为 w

x。如此，则有了 θ

x = w

x + b。

也就是说除了 y 由 y =0变为 y = −1 外，线性分类函数跟 GQ;BbiB+ 回归的形式化表示

(x)=g(θ

x)=g(w

x + b) 没区别。

进一步，可以将假设函数 h

w,b

(x)=g(w

x + b) 中的 g(z) 做一个简化，将其简单映

射到 y = −1 和 y =1上。映射关系如下：

g(z)=

1 z ≥ 0

−1 z<0

URX8V

RXk 线性分类的一个例子

下面举个简单的例子，如图k所示，现在有一个二维平面，平面上有两种不同的数

据，分别用圈和叉表示。由于这些数据是线性可分的，所以可以用一条直线将这两类数

据分开，这条直线就相当于一个超平面，超平面一边的数据点所对应的 y 全是 −1 ，另

一边所对应的 y 全是 R。

剩余51页未读，继续阅读

评论收藏

内容反馈

资源评论

资源反馈

评论星级较低，若资源使用遇到问题可联系上传者，3个工作日内问题未解决可申请退款~

Bertha_shar

粉丝: 2
资源: 3

上传资源快速赚钱

我的内容管理展开

我的资源快来上传第一个资源

我的收益

登录查看自己的收益

我的积分登录查看自己的积分

我的C币登录后查看C币余额

我的收藏

我的下载

下载帮助

前往需求广场，查看用户热搜

支持向量机通俗导论

支持向量机通俗导论.pdf

从零构建支持向量机(SVM) & 支持向量机通俗导论

支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版_2015.1.9.pdf

支持向量机通俗导论（理解SVM的三层境界）PDF

支持向量机通俗导论1

支持向量机通俗导论（理解SVM的三层境界）

支持向量机通俗导论（理解SVM的三层境界）Latex版.zip_SVM_python_支持向量机

支持向量机通俗导论（理解SVM的三层境界）Latex版

支持向量机通俗导论 理解SVM的三层境界

支持向量机通俗导论（理解SVM的三层境界）Latex版.zip_machine learning_svm精髓_支持向量机

支持向量机通俗导论 -- 理解SVM的三层境界

支持向量机通俗导论(SVM三层境界)-2018最新LaTex版

支持向量机通俗导论（理解SVM的三层境界）Latex版PDF

支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版_2015.1.91

数据挖掘与分析算法 支持向量机通俗导论（理解SVM的三层境界）共51页.pdf

支持向量机通俗导论（理解SVM的三层境界）-附件资源

python大作业 含爬虫、数据可视化、地图、报告、及源码（整和为一个文件）（2014-2020全国各地区原油加工量）.rar

仿真电路以及操作方法

最新资源

支持向量机通俗导论理解SVM的三层境界

数据挖掘与分析算法支持向量机通俗导论（理解SVM的三层境界）共51页.pdf

python大作业含爬虫、数据可视化、地图、报告、及源码（整和为一个文件）（2014-2020全国各地区原油加工量）.rar