SAS学习系列22.-一元线性回归.docx

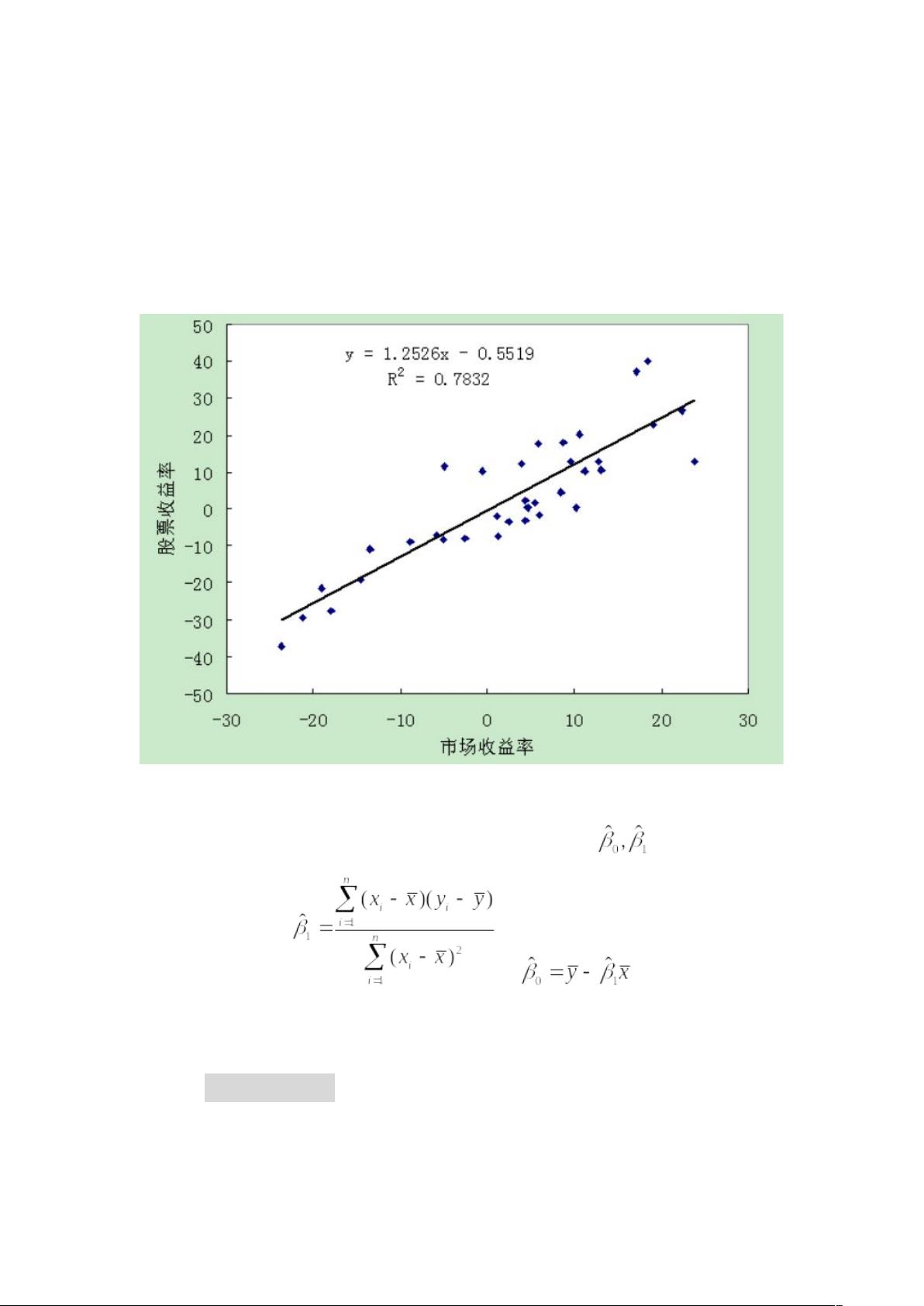
SAS学习系列22.-一元线性回归 一元线性回归是研究一个或多个变量（因变量）与另一些变量（自变量）之间关系的统计方法。主要思想是用最小二乘法原理拟合因变量与自变量间的最正确回归模型，得到确定的表达式关系。其作用是对因变量做解释、控制、或预测。 回归分析的步骤： 1. 获取自变量和因变量的观测值； 2. 绘制散点图，并对异常数据做修正； 3. 写出带未知参数的回归方程； 4. 确定回归方程中参数值； 5. 假设检验，判断回归方程的拟合优度； 6. 进展解释、控制、或预测。 一元线性回归模型为Y=β0+β1X+ε，其中 X 是自变量，Y 是因变量，β0、β1是待求的未知参数，β0也称为截距；ε 是随机误差项，也称为残差，通常要求 ε 满足： 1. ε 的均值为 0； 2. ε 的方差为σ²； 3. 协方差 COV(εi, εj)=0，当 i≠j 时。 用最小二乘法原理，得到最正确拟合效果的值。 假设检验： 1. 拟合优度检验：总偏差平方和与其自由度、回归平方和与其自由度、残差平方和与其自由度。 2. 回归方程参数的检验：假设β1=0，那么 Y 不随 X 变化，此时回归方程无意义。要做如下假设检验：H0: β1=0, H1: β1≠0。 用回归方程做预测：得到回归方程后，预测 X=x0 处的 Y 值。预测区间为： 残差图分析：残差图就是以残差为纵坐标，某一个适宜的自变量为横坐标的散点图。回归模型中总是假定误差项是独立的正态分布随机变量，且均值为零和方差相等为σ²。如果模型适合于观察到的数据，那么残差作为误差的无偏估计，应根本反映误差的假设特征。 回归诊断： 1. 残差图分析：残差图应该在零点附近对称地密布，越远离零点的地方就疏散； 2. 共线性诊断：模型中两个或两个以上的自变量高度相关，从而引起最小二乘估计可能很不准确； 3. 误差的独立性：假设误差项不独立，那么回归模型的许多处理，包括误差项估计、假设检验等都将没有推导依据。 SAS 中使用 PROC REG 过程步来进行一元线性回归分析，可以计算回归方程的参数、残差平方和、F 统计量、t 统计量等，并且可以对残差进行诊断，检查模型的拟合优度和误差的独立性。