### 经典ARIMA时间序列简介 #### 平稳性概念及重要性 在时间序列分析中,**平稳性**是构建模型前的一个关键前提条件。所谓**平稳性**,是指时间序列的数据特性(例如均值、方差等)不随时间的变化而变化。具体来说,如果一个时间序列是平稳的,则意味着它在未来的走势能够按照现有模式延续下去。平稳性分为两种类型:**严平稳**和**弱平稳**。 - **严平稳**:指的是不论如何取样,时间序列的分布特性不随时间变化。一个典型的例子是**白噪声**,其中每个数据点都是独立同分布的,并且通常假定为正态分布,其期望为0,方差为某个固定值。 - **弱平稳**:则强调的是时间序列的均值、方差以及协方差不会随着时间的变化而发生变化。这里的关键是序列数据的依赖性(即自相关性)保持不变。 #### 差分法 当时间序列不具备平稳性时,我们可以通过**差分法**来实现平稳化处理。**差分法**的基本思想是对原始数据进行一系列的操作,使得结果序列变为平稳。最简单的方式是一阶差分,即计算时间序列在相邻两个时间点上的差值。通过这种操作,可以消除序列中的趋势成分,进而达到平稳化的目的。 #### 自回归模型(AR) **自回归模型**(Autoregressive Model, AR)是一种基于时间序列历史数据来预测未来值的方法。在AR模型中,当前时刻的观测值是由过去的观测值线性组合加上随机误差构成的。具体来说,对于一个p阶自回归过程(AR(p)),其数学表达式如下: \[ x_t = \alpha + \phi_1 x_{t-1} + \phi_2 x_{t-2} + ... + \phi_p x_{t-p} + \epsilon_t \] 其中,\( x_t \) 表示当前时刻的观测值,\(\alpha\) 是常数项,\(\phi_i\) 是自回归系数,\(\epsilon_t\) 是随机误差项。 需要注意的是,为了使AR模型有效,时间序列必须具备以下条件: - **平稳性**:序列数据必须是平稳的。 - **自相关性**:序列中的数据必须表现出一定的自相关性。如果自相关系数\(\phi_i\)小于0.5,则表明序列不适合使用AR模型进行预测。 - **预测相关性**:AR模型仅适用于那些与前期值有明显相关性的现象。 #### 移动平均模型(MA) **移动平均模型**(Moving Average Model, MA)关注的是自回归模型中的误差项的累加效应。对于一个q阶移动平均过程(MA(q)),其数学表达式为: \[ x_t = \mu + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + ... + \theta_q \epsilon_{t-q} + \epsilon_t \] 这里的\(\mu\) 是常数项,\(\theta_i\) 是移动平均系数,\(\epsilon_t\) 是随机误差项。移动平均模型能够有效平滑掉序列中的随机波动,使得预测更加稳定。 #### 自回归移动平均模型(ARMA) **自回归移动平均模型**(ARMA)是自回归模型和移动平均模型的结合体。其数学表达式为: \[ x_t = \alpha + \phi_1 x_{t-1} + \phi_2 x_{t-2} + ... + \phi_p x_{t-p} + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + ... + \theta_q \epsilon_{t-q} + \epsilon_t \] ARMA模型能够同时利用序列的历史值和误差项的信息进行预测。 #### 差分自回归移动平均模型(ARIMA) **差分自回归移动平均模型**(ARIMA)是ARMA模型的一种扩展,用于处理非平稳的时间序列数据。ARIMA(p,d,q)模型的具体形式为: - p:自回归项数 - d:差分次数 - q:移动平均项数 ARIMA模型的核心在于先通过差分操作将非平稳序列转化为平稳序列,然后再建立ARMA模型。差分次数d反映了将原始序列转化为平稳序列所需的差分操作次数。 #### 自相关函数(ACF)与偏自相关函数(PACF) - **自相关函数(ACF)**:度量序列中某一时刻的观测值与另一个时刻的观测值之间的线性相关性。ACF有助于判断序列是否存在自相关性。 - **偏自相关函数(PACF)**:进一步去除序列中其他变量的影响,仅保留两时刻观测值之间的直接相关性。PACF可以帮助确定AR模型的阶数。 #### 模型选择与残差检验 在选择ARIMA模型时,通常会参考**AIC**(Akaike Information Criterion)和**BIC**(Bayesian Information Criterion)准则。这两个准则都是用来衡量模型复杂度与拟合效果之间的平衡。一般来说,较低的AIC或BIC值表示模型的性能更好。 - **AIC**:考虑了模型复杂度和拟合优度,公式为:\[ AIC = 2k - 2\ln(L) \] - **BIC**:在AIC的基础上引入了样本大小n的影响,公式为:\[ BIC = k\ln(n) - 2\ln(L) \] 其中,\(k\) 表示模型参数的数量,\(n\) 是样本大小,\(L\) 是最大似然估计值。 此外,在构建ARIMA模型后,还需要对模型的残差进行检验,确保它们是平均值为0且方差为常数的正态分布。常用的方法是绘制**QQ图**,若数据点大致呈直线分布,则可以认为残差服从正态分布。 ARIMA模型是处理时间序列数据的强大工具,但正确使用这一模型需要仔细分析序列的平稳性、选择合适的模型阶数并进行适当的残差检验。
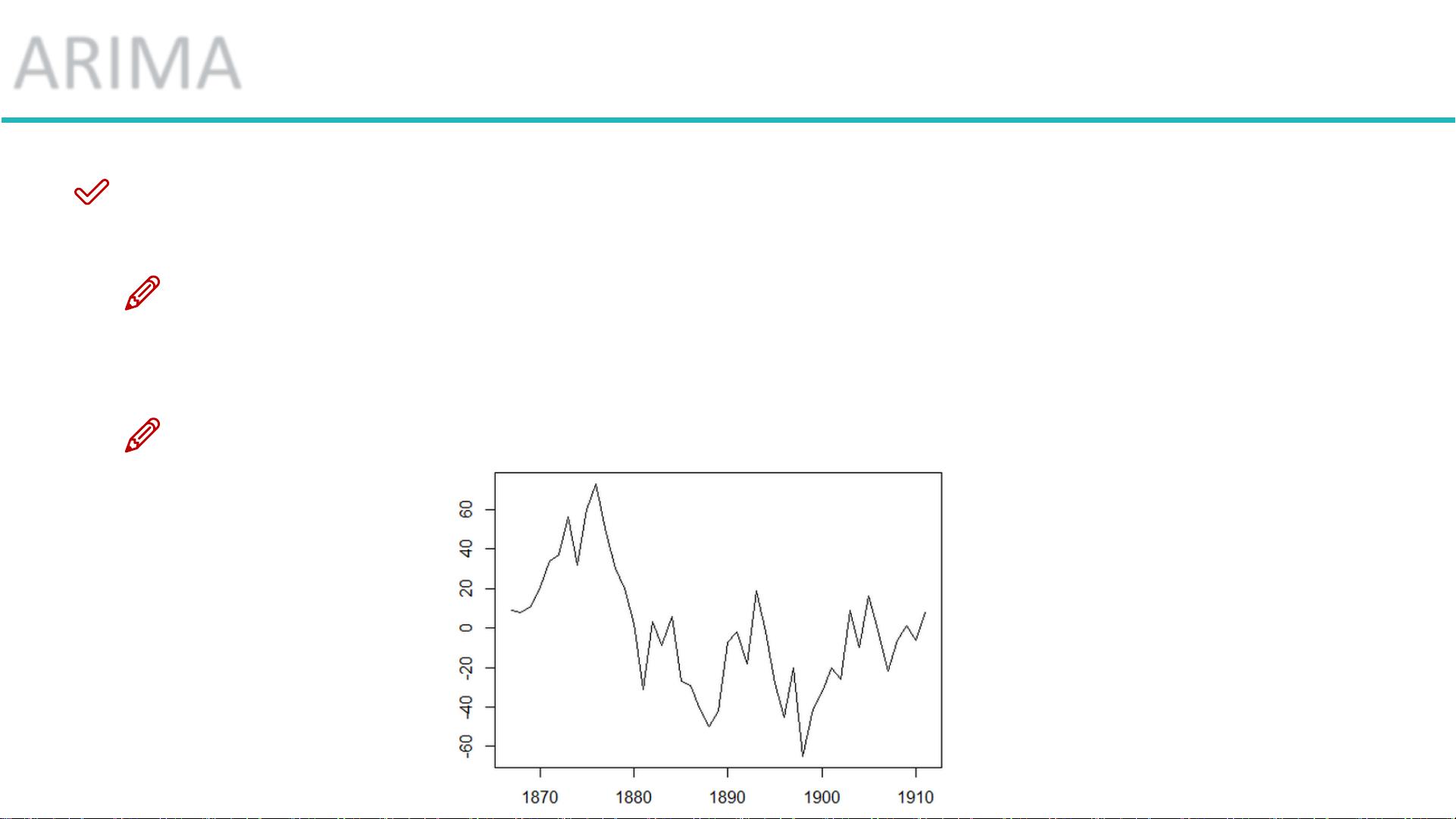

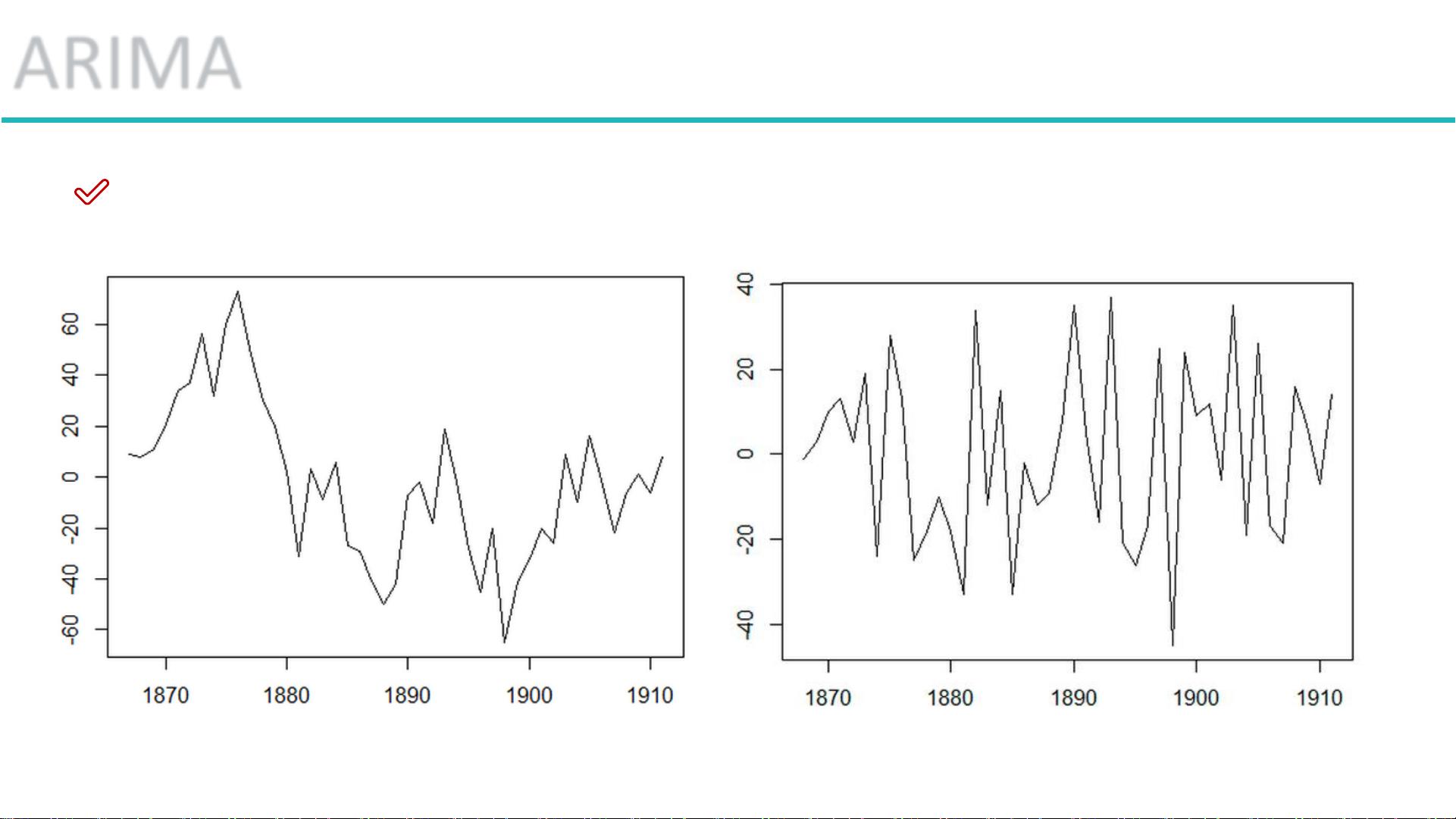
剩余14页未读,继续阅读

- 粉丝: 0
- 资源: 5
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功