第4届Mathorcup数学建模竞赛优秀论文-10376-10376a.pdf

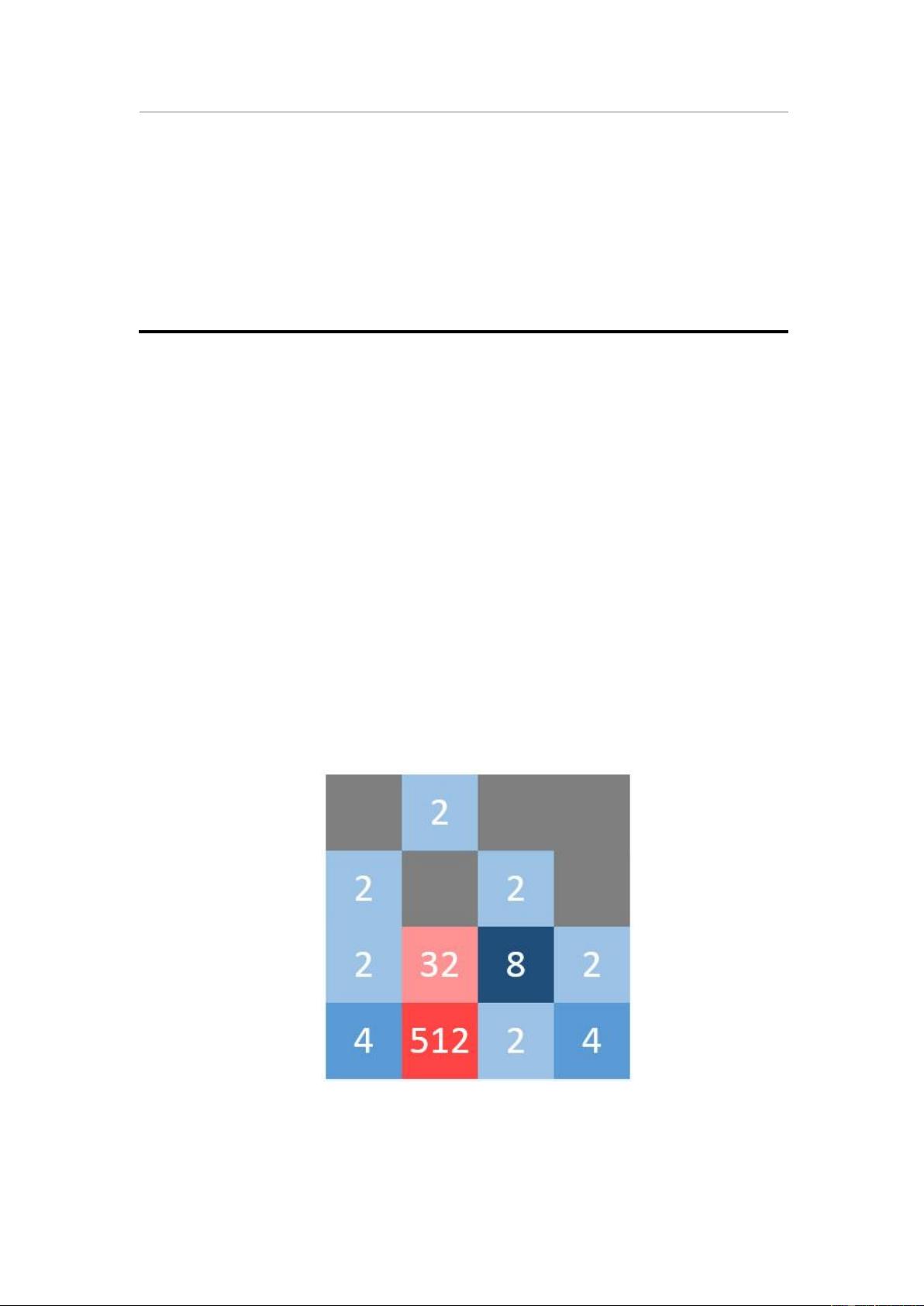
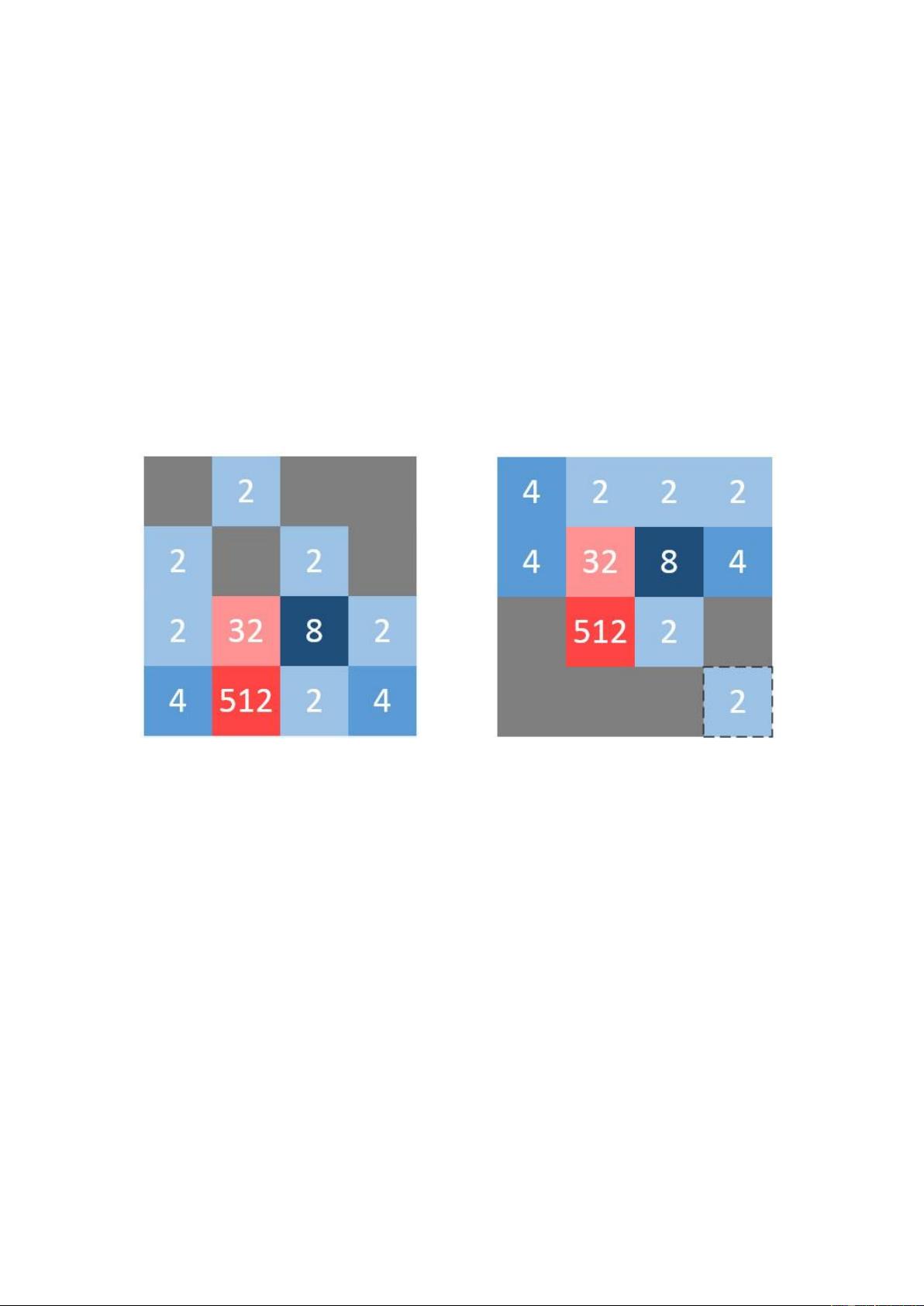
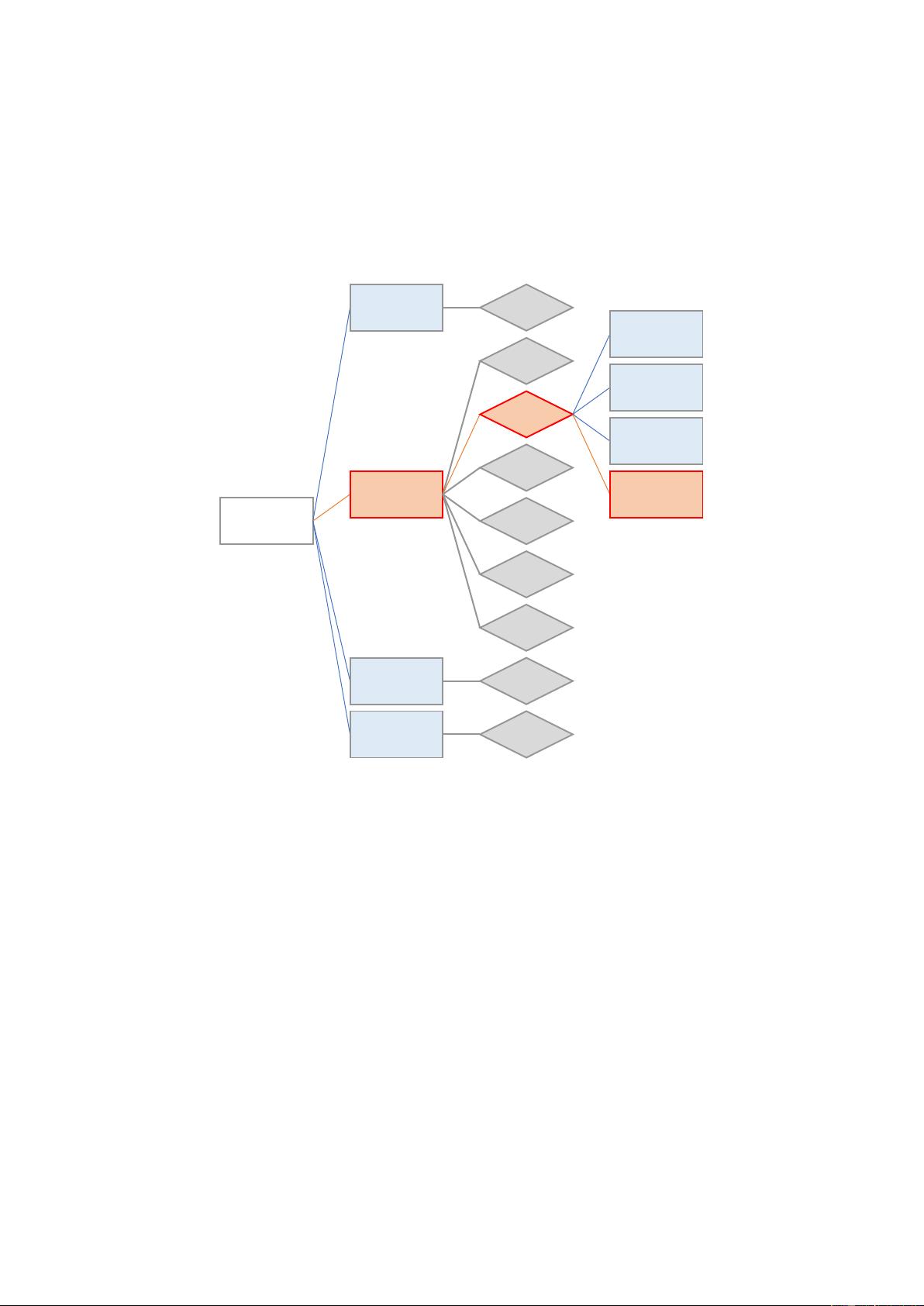
### 第4届Mathorcup数学建模竞赛优秀论文-10376-10376a.pdf #### 知识点提炼 ##### 1. **2048游戏介绍与模型建立** - **背景简介**：2048是一款网络上流行的策略游戏，以其简单直观的操作和富有挑战性的玩法而广受欢迎。玩家通过滑动屏幕上的数字方块（仅包含2的幂次），使相同数值的方块合并，目标是生成数值为2048的方块。 - **游戏规则**： - 玩家在4×4的方格盘上移动数字方块，每次操作可以向上、下、左、右四个方向之一移动所有非空方块。 - 当两个相同数值的方块相遇时，它们将合并成为一个数值等于两者之和的新方块。 - 每次玩家操作后，系统会在随机的空白位置生成一个数值为2或4的新方块。 - 游戏胜利条件是生成一个数值为2048的方块。 - 如果方格盘被填满且无法再进行任何有效移动，则游戏失败。 - **数学模型**：论文首先构建了一个游戏的博弈模型，分析了游戏双方（玩家和系统）的决策集合、游戏的博弈树以及决策分支。 - **理论分析**：良好的决策应该使得“在此决策前提下，之后进行随机决策，最后能到达2048”的概率最大化。 ##### 2. **估价指标的设计与应用** - **估价指标**：为了量化某个游戏局面的优劣，论文引入了一个简单的估价指标——盘面数值之和，用以衡量“从当前游戏局面出发，能够到达2048”的可能性。 - **特殊局面评估**：针对几个特殊的游戏局面，评估了估价指标的一些倾向性特征，以验证其合理性和实用性。 ##### 3. **Monte-Carlo随机模拟算法的应用** - **算法原理**：在某个决策分支点，对四个方向移动得到的新局面多次独立模拟一定步数的随机操作，进而得到一定步数后游戏格局估价指标的期望值估计。 - **实现细节**：利用MATLAB编程实现AI，并基于不同的取样值、模拟步数等参数调整，评估了算法的胜率。 - **评估指标**：通过移动次数和获胜概率等指标评估算法的表现。 ##### 4. **理论极限的探讨** - **最大数值**：论文分析了4×4盘面和N×N盘面理论上能够得到的最大数值，对于N×N盘面，这个数值是2^(N^2+1)。 - **进一步研究**：对于4×4盘面，探讨了获得2048之后继续进行游戏所能达到的最大数值，并将结果推广至任意N×N盘面的情况。 #### 结论 通过对2048游戏的深入分析，这篇论文不仅构建了一个有效的数学模型，还提出了一种基于Monte-Carlo随机模拟算法的AI解决方案。此外，对游戏理论极限的研究也为后续的相关研究提供了有价值的参考。整体而言，该论文提供了一套完整的方法框架，可用于指导类似游戏的AI开发和其他相关领域的研究。