
人工智能实验——经典 CNN 架构 实验报告
实验目标:
实现并理解几个 CNN 神经网络用于 MNIST 图像分类:LeNet、AlexNet、
VGGNet、GoogLeNet、ResNet。
简介:
本次实验通过实现了五种经典的 CNN 架构,加强了对 CNN 的理解,其中在
每个网络实现前都有一部分自己的理解,以及灰底部分的代码实现问题,每个模
型后均有参数调整的过程及结果。在模型对比部分分别对不同模型的效果及其原
因作了适当的分析。
实验环境
VSCode、Python、Pytorch
实验过程:
LeNet:
LeNet 的整体网络结构可以用一张图来概括,也就是下面这张 Yann LeCun 在
1998 年的论文中展示的图片:
图 1 Gradient-based learning applied to document recognition 中 LeNet 结构图
论文中采用了两层卷积层,两层池化层,三层全连接层进行训练。我将这个
网络结构理解为:两个卷积池化层(卷积后进行池化)以及全连接层(本文中是

三个全连接网络组成),其中卷积池化层的作用是提取特征图,全连接层则是模
型主要的参数所在。
LeNet 是最早出现的经典卷积神经网络,卷积操作就是为提取特征而被适用
于神经网络训练的。在绘画中,我们需要先打好画面框架,然后勾线,最后上色,
而卷积的操作其实就是将这些步骤逆着推,我们查看第一层卷积出的结果时可以
看出这很像是一种线稿(后面深度学习网络通常第一层是颜色、边缘特征,目的
性不同):
图 2 卷积操作可视化(参考北邮鲁鹏老师 PPT)
所以 LeNet 第一个卷积层就是为了得到一幅幅线稿(后面称之为特征响应
图),然后就是池化层,LeNet 论文中的池化层采用了平均池化(Average Pooling)
的方法,符合当时下采样兼顾各个像素点的启发式想法,但是在如今一般都采用
了最大池化(Max Pooling),且获得的效果通常来说更好,我们也可以像理解绘
画那样,思考一下绘画中构图搭建框架的时候,通常先是不管细节的,细节其实
对整幅画作只起到了美观的作用,而不是识别出画作需要细节,就比如勾勒人物
轮廓只需要一条细线即可,但是在打磨细节时需要稍稍将其加粗;MNIST 手写
数据集的粗细其实并不影响识别。因此我们隔几个像素取其中最大的(也是最有
特征的)像素点作为特征放入下一层可能得到的效果更好,实验证明确实如此。
全连接网络作为更早提出的一种机器学习方法,是一种类似拟合函数的方法,
由于反向传播的提出,这变成了一种准确率较高的黑盒模型,这里不多赘述细节。
全连接网络最大的诟病是容易过拟合和参数太多,但是我们可以设想,只要我们
给全连接神经网络的数据够多,其算力够强,完全是可以模拟出任何函数的,而
数据够多也就变相解决了过拟合问题。因此全连接神经网络可以说是神经网络模
型的基础,但问题就是算力不够,数据不够,因此需要卷积层来提取特征,减小
训练数据。
在 LeNet 中,第一个卷积池化层就像是提取线稿,第二个卷积池化层就像是

提取框架,然后放入全连接网络中进行训练,“拟合”出一个函数。
第一个卷积池化层:
在论文中,第一个卷积层卷积核大小为 5*5*1,个数为 6,步长为 1,补充两
个 zero padding,第一个池化层大小为 2*2,步长为 2。
self.conv_pool_1 = nn.Sequential(
# 卷积层 (1*28*28) -> 6*28*28)
nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5,
stride=1, padding=2),
nn.ReLU(),
# 池化层 (6*28*28) -> (6*14*14)
nn.MaxPool2d(kernel_size=2, stride=2)
)
第二个卷积池化层:
在论文中,第二个卷积层大小为 5*5*6,个数为 16,步长为 1,无 padding,
池化层大小为 2*2,步长为 2。
self.conv_pool_2 = nn.Sequential(
# 卷积层 (6*14*14) -> (16*10*10)
nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5,
stride=1, padding=0),
nn.ReLU(),
# 池化层 (16*10*10) -> (16*5*5)
nn.MaxPool2d(2, 2)
)
全连接层:
在论文中,第一个全连接层有 120 个输出,第二个全连接层有 84 个输出,
第三个全连接层即类别个数。
self.fc = nn.Sequential(
# 将卷积池化后的 tensor 拉成向量
nn.Flatten(),
# 全连接层 16*5*5 -> 120
nn.Linear(16 * 5 * 5, 120),
nn.ReLU(),
# 全连接层 120 -> 84
nn.Linear(120, 84),
nn.ReLU(),
# 全连接层 84 -> 10
nn.Linear(84, 10)
)
在本次实验中, LeNet 的复现并未使用 Average Pooling,采用了更合适的
Max Pooling(理由在上面提到),激活函数则使用了 ReLU,因为如果使用 Sigmoid
激活,网络很容易出现梯度消失(再加上 Average Pooling 效果更差,故不做展
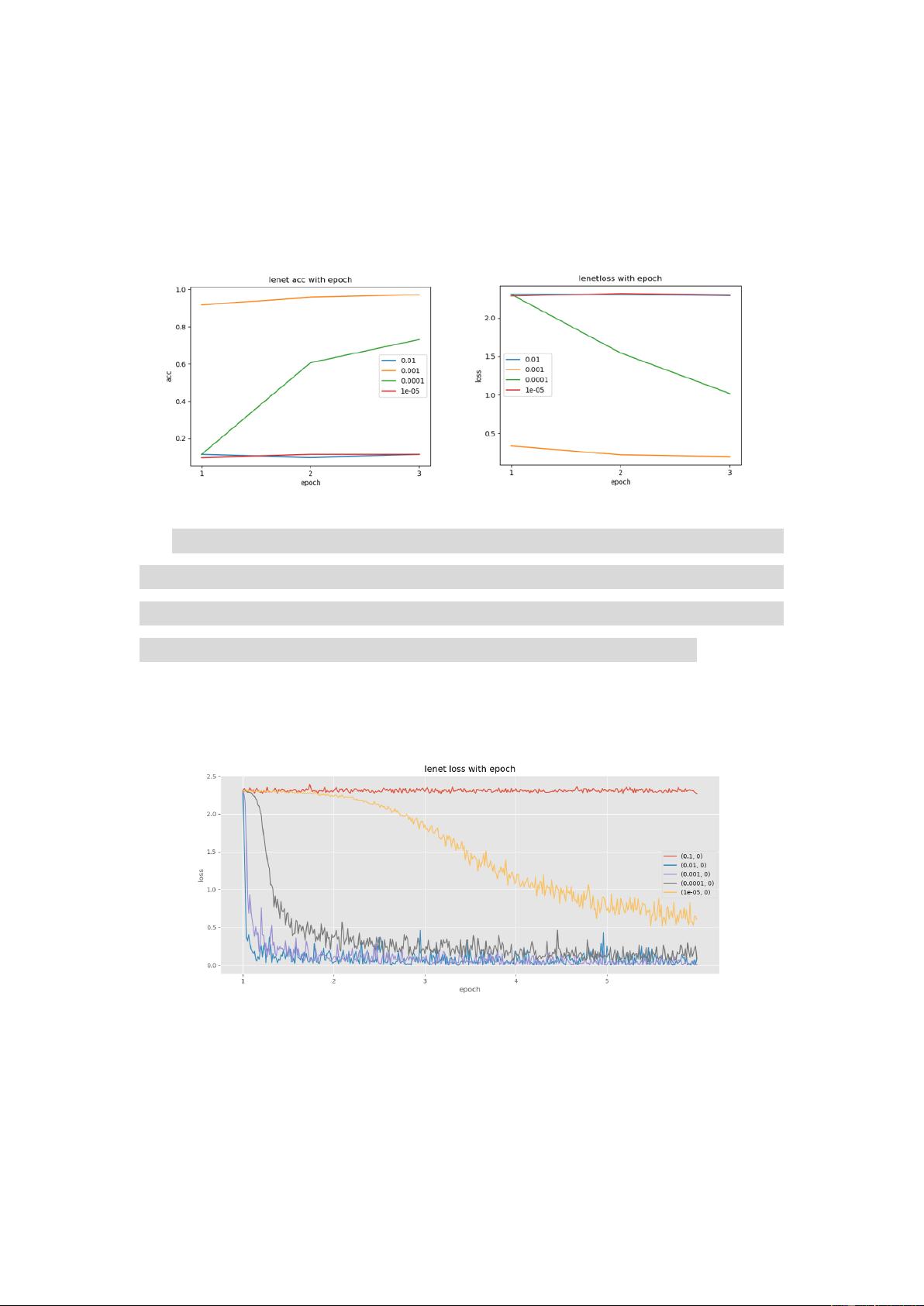
示),可以看到 learning rate 大于 0.01 或者小于 1e-5 的时候就无法训练了:
图 3 LeNet 使用 Sigmoid 激活时 acc/loss 随 epoch 的变化(不同学习率)
在起初的实验过程中,由于在 nn.Sequential 中未放入 ReLU 函数(因为以为
Pytorch 会自动补上,后面查证资料与实验验证是会在每个自定义的层后面补上,
即上述例子的 conv_pool_1 后会补加 ReLU,而 Sequential 内部并不会补加),导
致训练结果较差,之后在每一层全连接层后添加 ReLU 解决此问题。
LeNet 实验结果(由于实验模型中无 dropout,因此并不将其作为超参):
图 4 LeNet 使用 ReLU 激活时 loss 随 epoch 的变化(不同学习率)
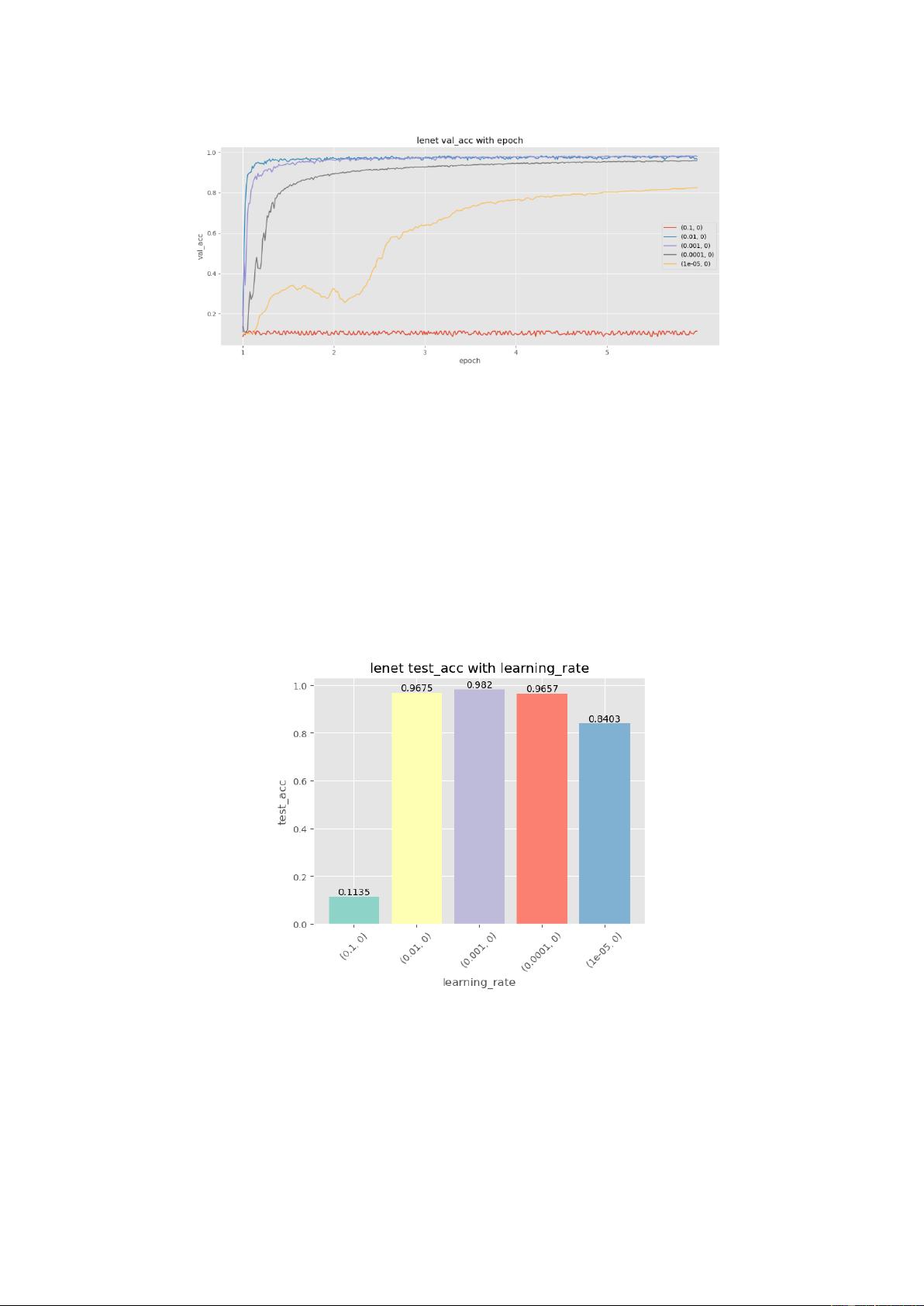
图 5 LeNet 使用 ReLU 激活时 acc 随 epoch 的变化(不同学习率)
在实验中,当学习率大于 0.1 时 acc 和 loss 会几乎保持不变,虽然使用了
Adam 优化器,但是学习率过大依旧会造成参数根本无法学习,由于学习率太大
会导致梯度更新的时候过大,进而导致梯度爆炸;学习率小于 1e-5 时学习较慢。
因此这个模型我们采用 0.01 或者 0.001 的学习率训练就可以了,但是 0.001
从 loss 和 acc 的趋势来说更稳定,因此在最后模型比较时选择 0.001 作为超参
数。
最后这五组参数在测试集上的结果:
图 6 LeNet 在测试集的表现
AlexNet:
AlexNet 首次使用了 ReLU 激活函数和 dropout,并采用了 GPU 训练,但是
本次实验中将下图架构中的两个并行训练网络合并成一个,并调整了原论文的参
数,因为原始参数不适合这 MNIST 数据集。



















