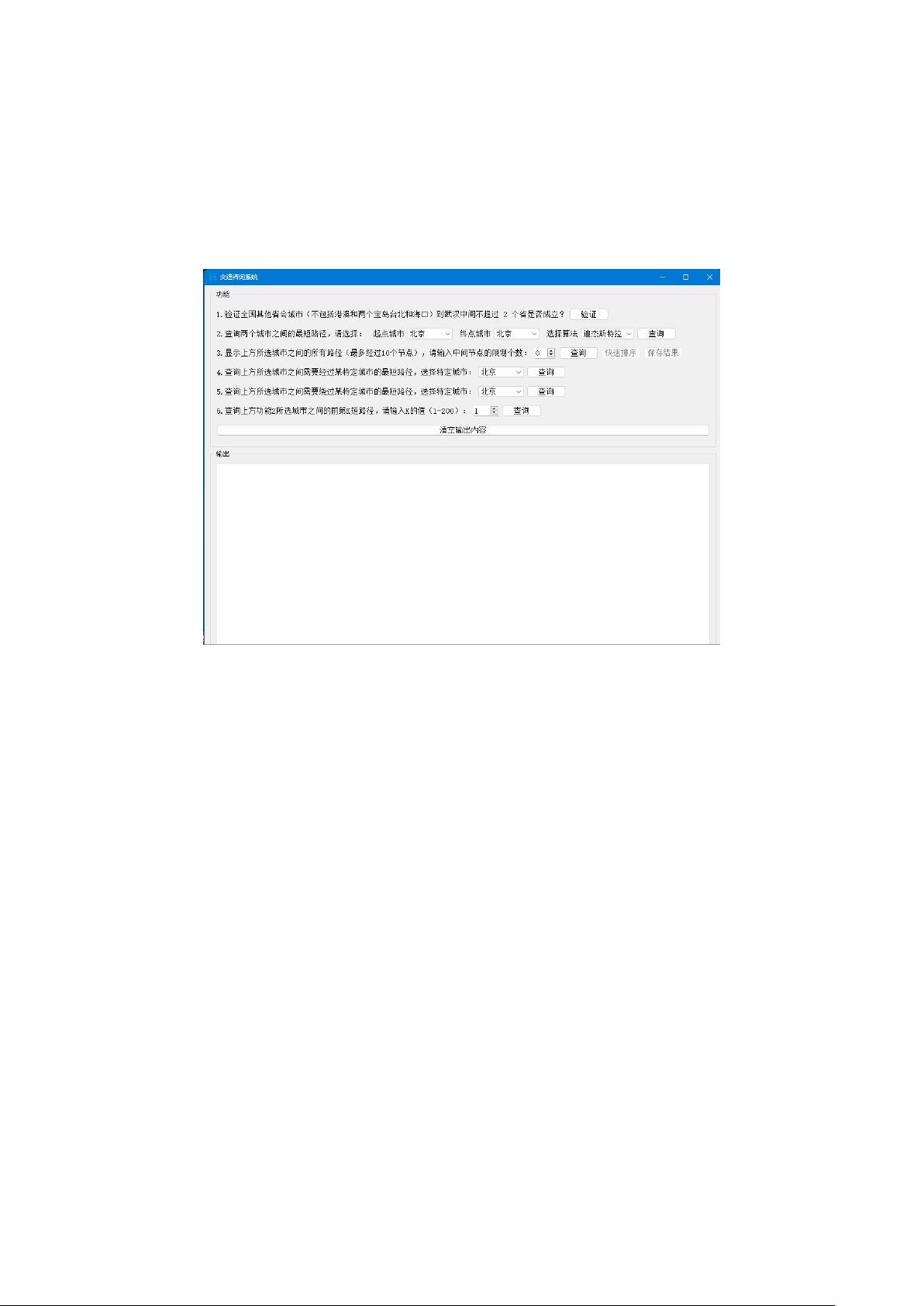
一 题目要求
题目设计目的:熟练掌握迪杰斯特拉算法和费洛伊德算法,能够利用它们解决最短路径
问题。掌握图的深度,广度遍历算法。掌握快速排序算法。
问题描述:设计一个交通咨询系统,通过读取全国城市距离图(省会城市邻接矩阵.xlsx,
请在程序运行时动态加载到内存,可将 excel 转成 csv 方便读取)。
具体功能为:1、请验证全国其他省会城市(不包括港澳和两个宝岛台北和海口)到武
汉中间不超过 2 个省(省会城市)是否成立?2、允许用户查询从任一个城市到另一个城市
之间的最短路径(两种算法均要实现,界面上可自行选择)以及所有不重复的可行路径(可
限制最多经过 10 个节点),并利用快速排序对所有路径方案依据总长度进行排序输出(输
出到文件),每一条结果均需包含路径信息及总长度,试比较排序后的结果与迪杰斯特拉算
法和费洛伊德算法输出的结果;3、假设在求解 2 个城市间最短路径时需要绕过某个特定的
城市(用户输入或者选择,例如武汉),请问应该如何实现?4、不基于功能 2 遍历的结果
如何直接求解两个城市间的前第 K 短的路径,例如,武汉到北京之间第 3 短的路径。
二 需求分析
2.1. 存图
我采用 C++来实现本系统,在 C++中,保存图的数据结构通常有两种常见的选择:邻
接矩阵和邻接表。邻接矩阵的话是使用二维数组来表示图中各个节点之间的关系,如果图是
稠密的(边的数量接近节点数量的平方),那么邻接矩阵是一个不错的选择,并且邻接矩阵
存储的空间复杂度较高,为 O(V^2),其中 V 是节点的数量。邻接表的话是使用链表或数组
的数组来表示图中的每个节点以及与之相邻的节点,对于稀疏图(边的数量远小于节点数量
的平方),邻接表是更有效的选择,其空间复杂度为 O(V + E),其中 V 是节点的数量,E 是
边的数量。
分析数据可知,全国省会城市以及直辖市共有 34 个(包含港澳台),也就是说我们构建
的无向图顶点数量也是 34 个,但是城市与城市之间连接的边的数量远远大于顶点的数量,
因此我将采用邻接矩阵来保存图。
为了读取更加方便,我先将“省会城市邻接矩阵.xlsx”中的省会城市距离邻接矩阵和省会
城市邻接矩阵都转换为 CSV 格式,然后分别读取这两个 CSV 文件,将读取结果保存到两个
邻接矩阵中,对于省会城市邻接矩阵,两城市之间存在直达路径,则边的权值为 1,否则为
0,城市自身到自身的权值也为 1。对于省会城市距离邻接矩阵,由于表格中给出的数据为
城市之间的距离,包括非直达的路径,因此需要根据省会城市邻接矩阵将省会城市距离邻接
矩阵中的数据处理一下:如果省会城市邻接矩阵中的值为 0,则代表两城市不相邻,那么就
将省会城市距离邻接矩阵中对应的值改为 INF(无穷大),另外,城市自身到自身的距离设
置为了 1。