2013年美国大学生数学建模大赛A题 一等奖.pdf
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
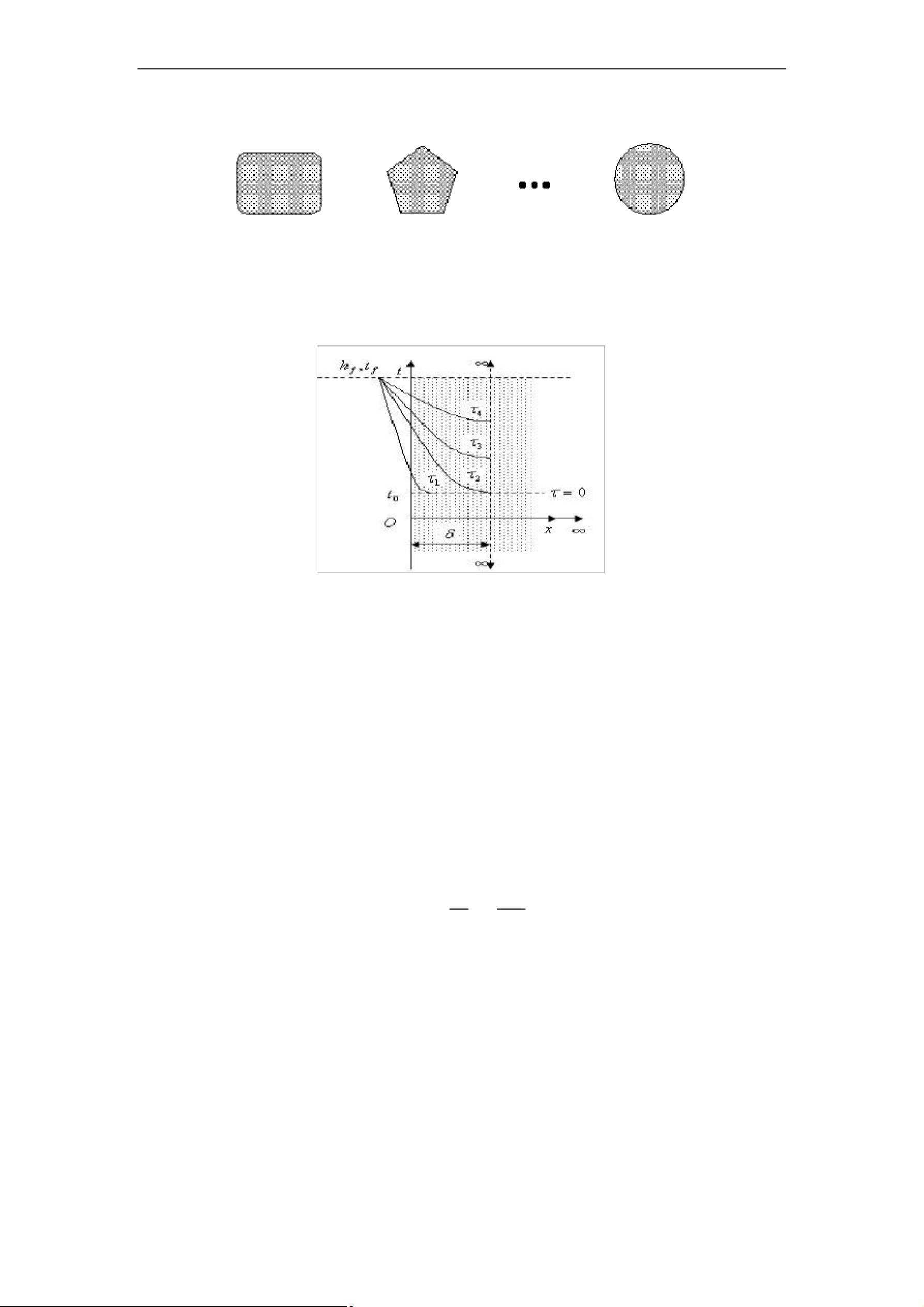
【2013年美国大学生数学建模大赛A题】主要关注的是如何通过数学建模解决实际问题,尤其是关于烹饪中的布朗尼蛋糕烘焙问题。该题目的获奖论文深入研究了烤盘的最佳形状以确保最理想的烘焙效果。以下是论文中涉及的主要知识点: 1. **热量分布模型**:为了确定最佳烤盘形状,团队首先构建了一个热量分布模型,考虑了烤盘在加热过程中的热传导。他们将烤盘的一条边视为半无限大平板,应用非稳态导热公式(第三边界条件),分析了不同形状烤盘的热量分布。结果表明,烤盘形状从多边形趋向圆形时,烤焦的程度逐渐减小。 2. **数量最优模型**:该模型旨在找出烤箱能容纳的最大烤盘数。论文中通过建立一个与烤箱长宽比和烤盘边数相关的函数来解决这个问题。模型显示,烤盘数量与烤箱长宽比和边数有直接关系,且在特定比例下,烤盘数量可达到最大化。 3. **热量分布最优模型**:为了优化烤盘的热量均匀性,团队定义了平均热量分布H,即未烤焦区域在烤盘边缘总面积中的占比。他们发现,随着烤箱长宽比和形状的变化,平均热量分布有其特定的函数关系。特别地,圆形烤盘在热量分布上表现最优。 4. **数量与热量混合最优模型**:为了兼顾烤盘数量和热量分布,论文建立了最后一个模型,通过无量纲化处理两个关键函数(烤盘数量与热量分布),并引入权重p来平衡两者的重要性。通过求解,得出在特定的W/L值和p值下,六边形烤盘是最优选择。 5. **问题分析**:论文分析了在有限空间内的烤盘热量分布问题,假设烤箱在工作时内部温度均匀。团队利用一维非稳态导热理论和多维非稳态导热的乘积解法,对多边形烤盘进行二维热量分布模拟,从而评估不同形状烤盘的烘焙效果。 6. **几何优化**:烤盘数量的最大化问题转化为在固定面积W×L内多边形的平铺问题。通过研究不同烤盘边数和烤箱长宽比的组合,团队找出了在特定条件下烤盘排列最密集的方案。 这篇论文展示了数学建模在解决实际问题中的应用,特别是如何通过数学工具优化烹饪过程,以获得最佳烘焙效果。它涉及了热力学、几何学和优化理论等多个领域的知识,体现了数学在解决跨学科问题时的强大能力。


剩余16页未读,继续阅读

 lyrics8862023-01-11超级好的资源,很值得参考学习,对我启发很大,支持!
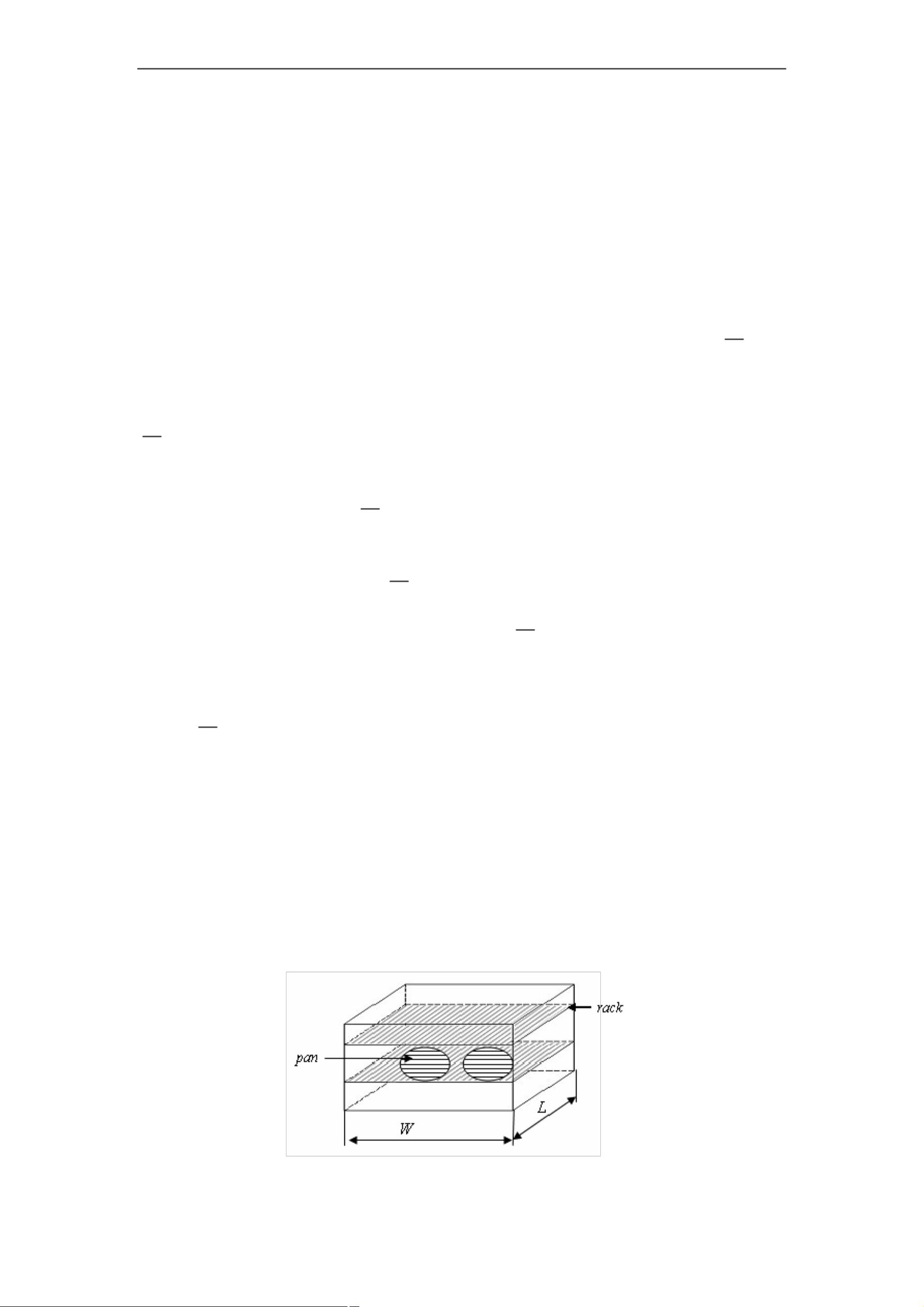
lyrics8862023-01-11超级好的资源,很值得参考学习,对我启发很大,支持!
- 粉丝: 6911
- 资源: 3万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功