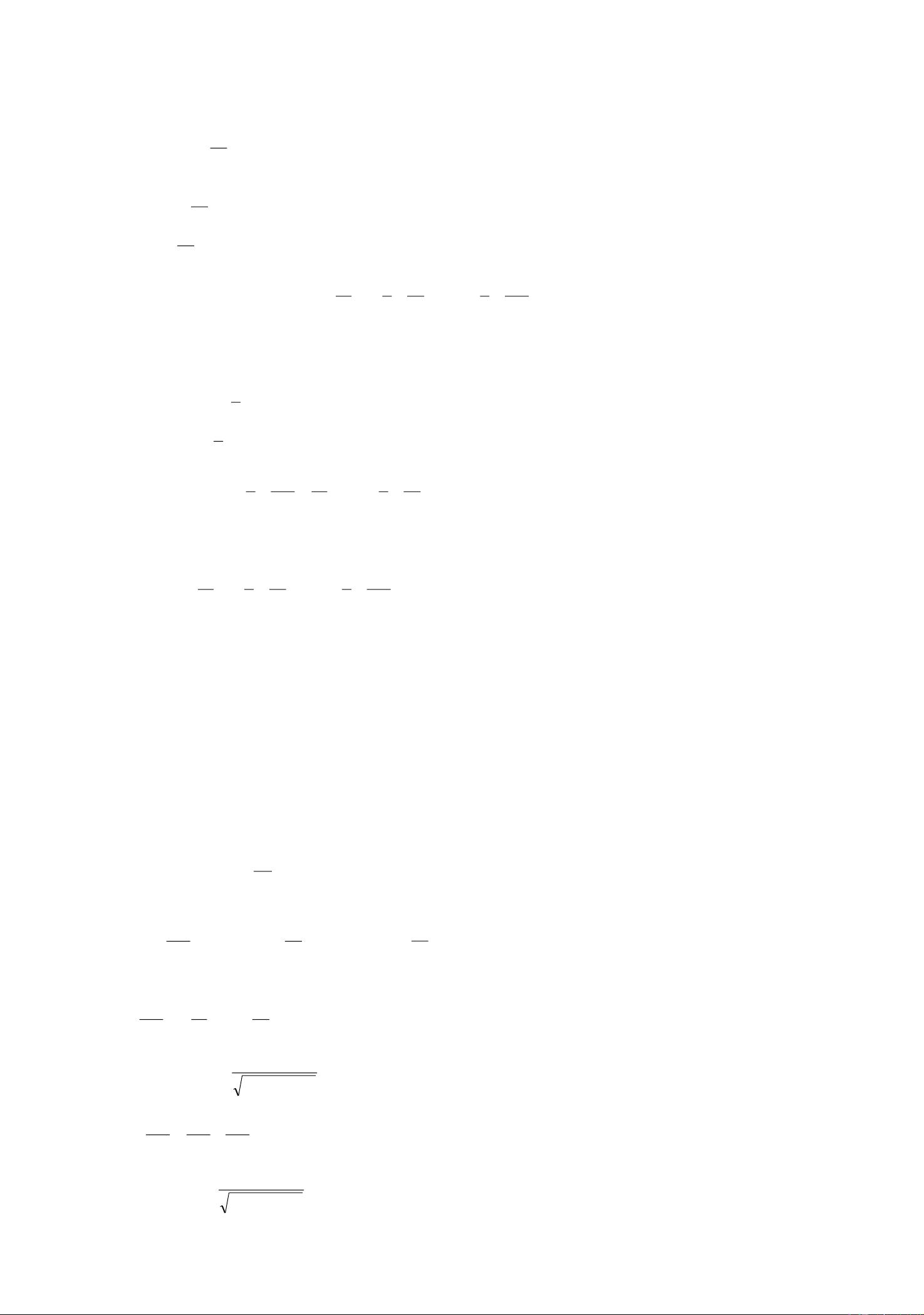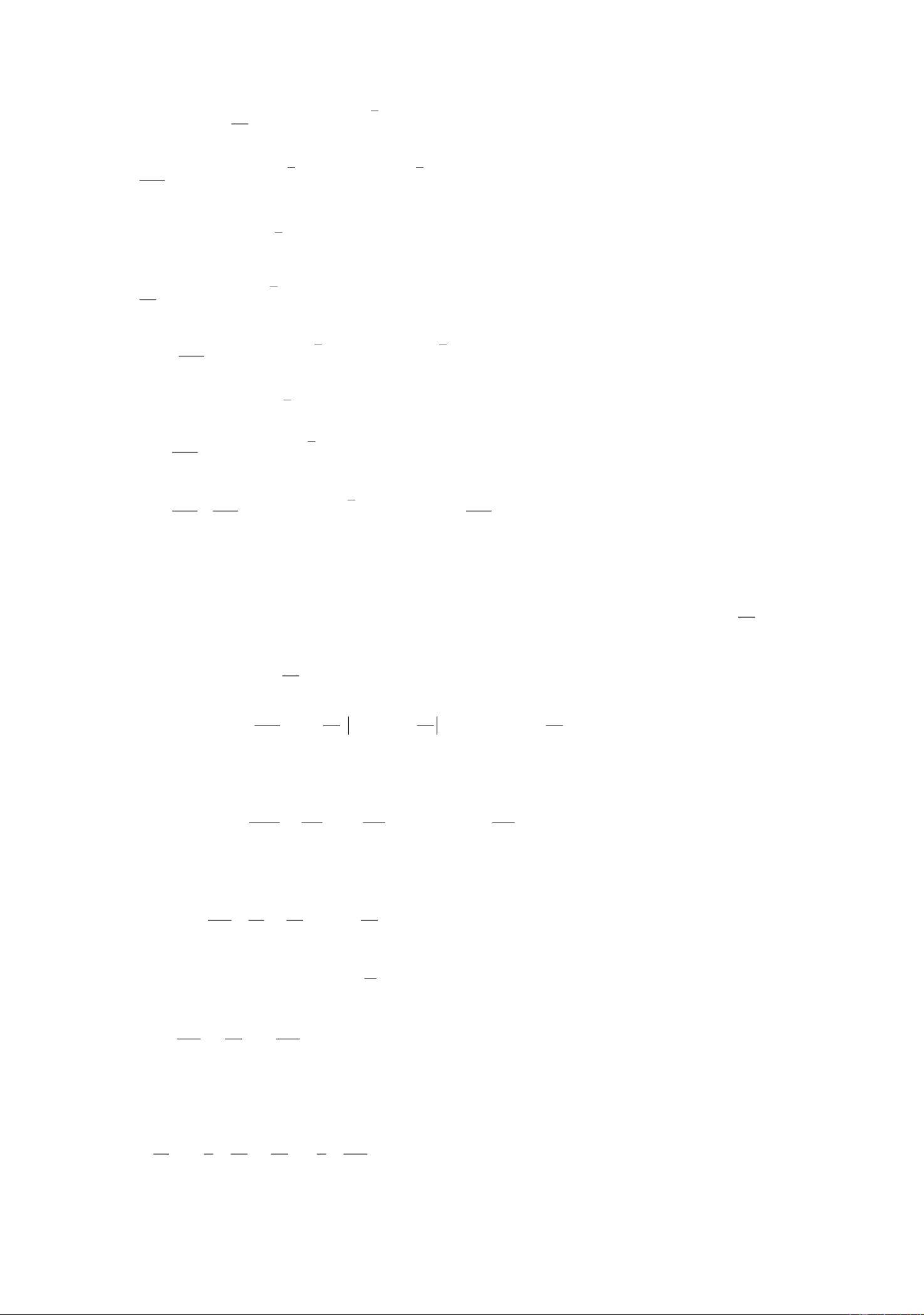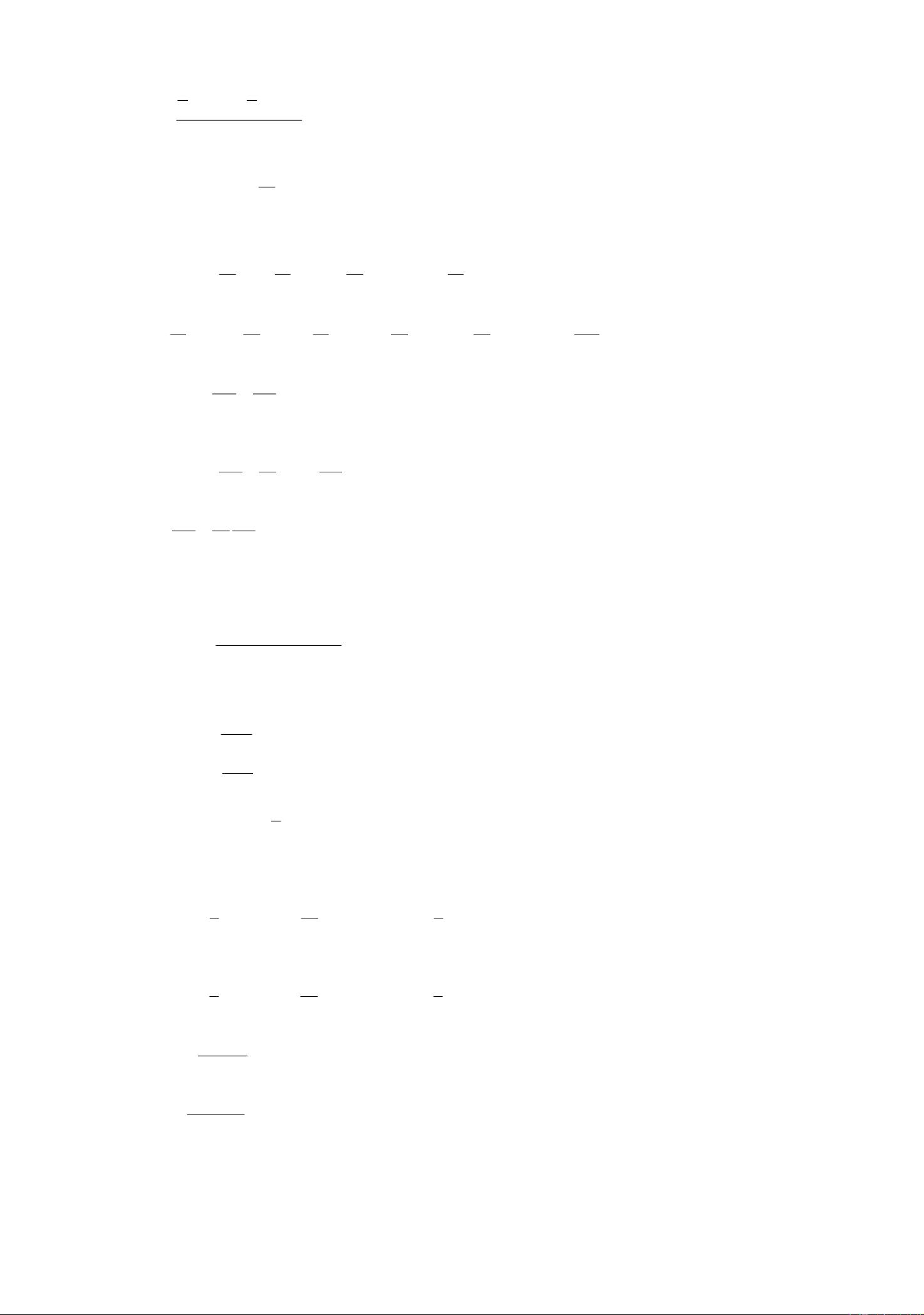数学物理方程（第二版）谷超豪等（答案1-4章）.pdf

在物理学中，数学方程的运用是描述和解释自然界现象的重要工具。在研究波动、振动等问题时，数学物理方程成为了分析这些现象的核心。由谷超豪等编写的《数学物理方程》第二版，是一本在科学界广受推崇的教科书，它系统地介绍了波动方程、边界条件、纵振动方程、横振动方程等多种数学物理方程，并对这些方程在不同条件下的应用进行了详细阐述。本文将围绕该书的前四章内容，深入探讨这些数学物理方程的基本概念、方程形式及其应用。 波动方程作为描述波动传播的基础方程，在物理和工程学中有着广泛的应用。在数学物理方程中，波动方程的一般形式为ttuxsx)()(xESutx=，其中u(x,t)代表波动的位移，x为位置坐标，t为时间变量。通过该方程，我们可以推导出波动在不同介质中的传播速度和形态，而波动的位移u(x,t)是波动状态的关键函数，其变化反映了波动的动态过程。波动方程的求解通常需要借助边界条件，这些条件规定了波动在空间区域边界上的具体行为，例如端点固定、自由端点或弹性支承等。这些边界条件对波动方程的解有着重要影响，它们限定了波动可能存在的形式和传播的模式。 接着，本资源还深入探讨了圆锥形枢轴的纵振动方程。圆锥形枢轴在某些工程结构中有着重要应用，其纵振动方程的推导和应用对于理解这类结构的动态响应至关重要。纵振动方程具有形式2222)1(])1[(tuhxxuhxxE−=−，其中h表示圆锥的高，x为空间坐标，u(x,t)为波动的位移，E为杨氏模量，为圆锥的密度。通过对方程的分析和求解，我们可以了解圆锥形枢轴在受到外力作用时的振动特性。 另一个重要方程是弦线的微小横振动方程，该方程用于描述在微小振动情况下，弦线上各点的位移变化。其方程形式为)][(22xuxlxgtu−=，x为空间坐标，t为时间，l为弦线长度，g为重力加速度，为弦线密度。弦线的振动方程不仅揭示了弦线振动的基本规律，而且在音乐乐器、桥梁结构等领域中有着广泛的应用。 本资源还讨论了波动方程在特定区域的应用，例如在锥形区域中的应用。在此情况下，波动方程展现出了其特殊形式，例如函数2221),,(yxttyxu−−=在锥形区域222yxt−−>0中的行为。这类问题的研究不仅涉及波动方程，还涉及到特定几何形状区域内的波动传播特性，因此其求解通常更为复杂。 通过对数学物理方程的系统学习，读者可以掌握波动、振动等现象的数学描述和分析方法，从而在物理、工程等多个领域中更准确地模拟和预测现象的动态行为。《数学物理方程》第二版通过严谨的逻辑推理和丰富的实例，为读者提供了一个深入了解和应用这些方程的平台，极大地促进了数学与物理学的交叉研究与应用。