matlab优化工具箱介绍_matlab运算实例源码.doc

Matlab 优化工具箱介绍 Matlab 优化工具箱（Optimization Toolbox）是 Matlab 的一个功能强大的工具箱，主要应用于解决各种优化问题。它提供了许多函数来解决无约束非线性极小值、约束条件下非线性极小值、二次规划和线性规划问题、非线性最小二乘逼近和曲线拟合等问题。 1. 优化工具箱简介 Matlab 优化工具箱主要应用包括： * 求解无约束非线性极小值 * 求解约束条件下非线性极小值，包括目标逼近问题、极大-极小值问题 * 求解二次规划和线性规划问题 * 非线性最小二乘逼近和曲线拟合 * 求解复杂结构的大规模优化问题 优化工具箱的常用函数包括： * fminbnd：求解多变量函数的最小化 * fminunc：求解无约束非线性最小化 * fminsearch：求解线性线性规划问题 * linprog：求解二次规划问题 * quadprog：求解有约束的非线性最小化 * fmincon：求解多目标规划的优化问题 * fgoalattain：求解最小、最大化问题 * fminimax：求解有约束的非线性最小化 2. 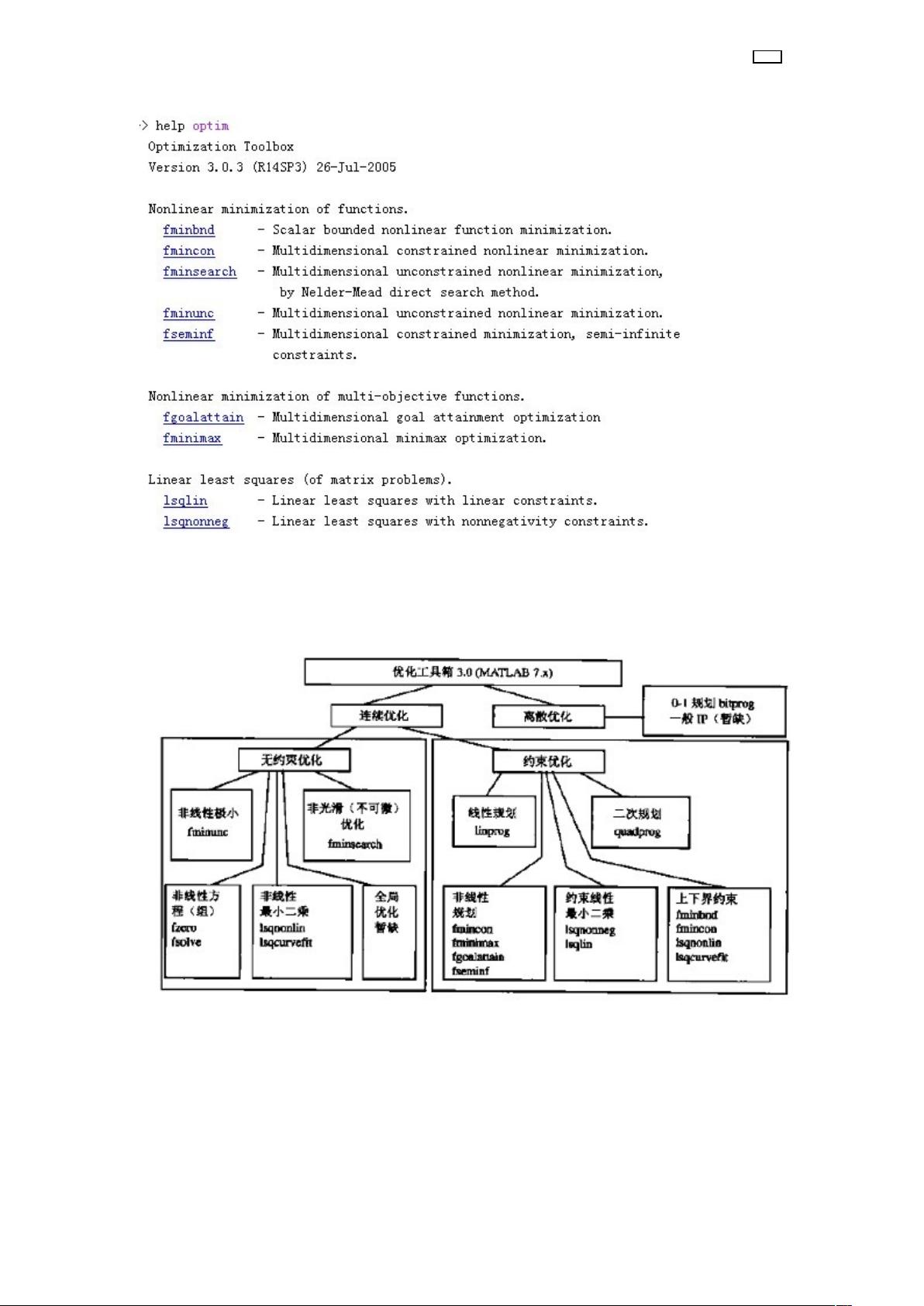Matlab 优化函数的查阅与定位 在 Matlab 的命令窗口键入命令 help optiom，可以显示该工具箱中所有函数清单。 3. 优化工具箱的结构 优化工具箱的结构包括： * 优化函数：提供了许多函数来解决各种优化问题 * 优化算法：提供了多种优化算法，例如梯度下降法、牛顿法等 * 优化参数设置：提供了多种参数设置，例如迭代次数、终止条件等 4. 优化函数简介 4.1 线性规划问题 线性规划问题是目标函数和约束条件均为线性函数的问题。线性规划问题的数学模型为： min nRxxf s.t.：bxA* beqxAeq* ubxlb* 其中 f、x、b、beq、lb、ub 为向量，A、Aeq 为矩阵。 函数 linprog 的调用格式为： x = linprog(f,A,b) x = linprog(f,A,b,Aeq,beq) x = linprog(f,A,b,Aeq,beq,lb,ub) x = linprog(f,A,b,Aeq,beq,lb,ub,x0) x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options) 4.2 非线性规划问题 多元函数最小值的数学模型为： min f(x) 其中 x 为向量。 函数 fminbnd、fminsearch 和 fminunc 可以用于解决无约束非线性规划问题。 函数 fminbnd 的调用格式为： x = fminbnd(fun,x1,x2) x = fminbnd(fun,x1,x2,options) [x,fval] = fminbnd(…) [x,fval,exitflag] = fminbnd(…) [x,fval,exitflag,output] = fminbnd(…) 函数 fminsearch 和 fminunc 的调用格式类似。 Matlab 优化工具箱是一个功能强大的工具箱，提供了许多函数和算法来解决各种优化问题。它广泛应用于科学研究、工程设计、经济金融等领域，具有很高的经济效益和社会效益。