极大似然 S函数 逻辑回归 具体案例 学习笔记

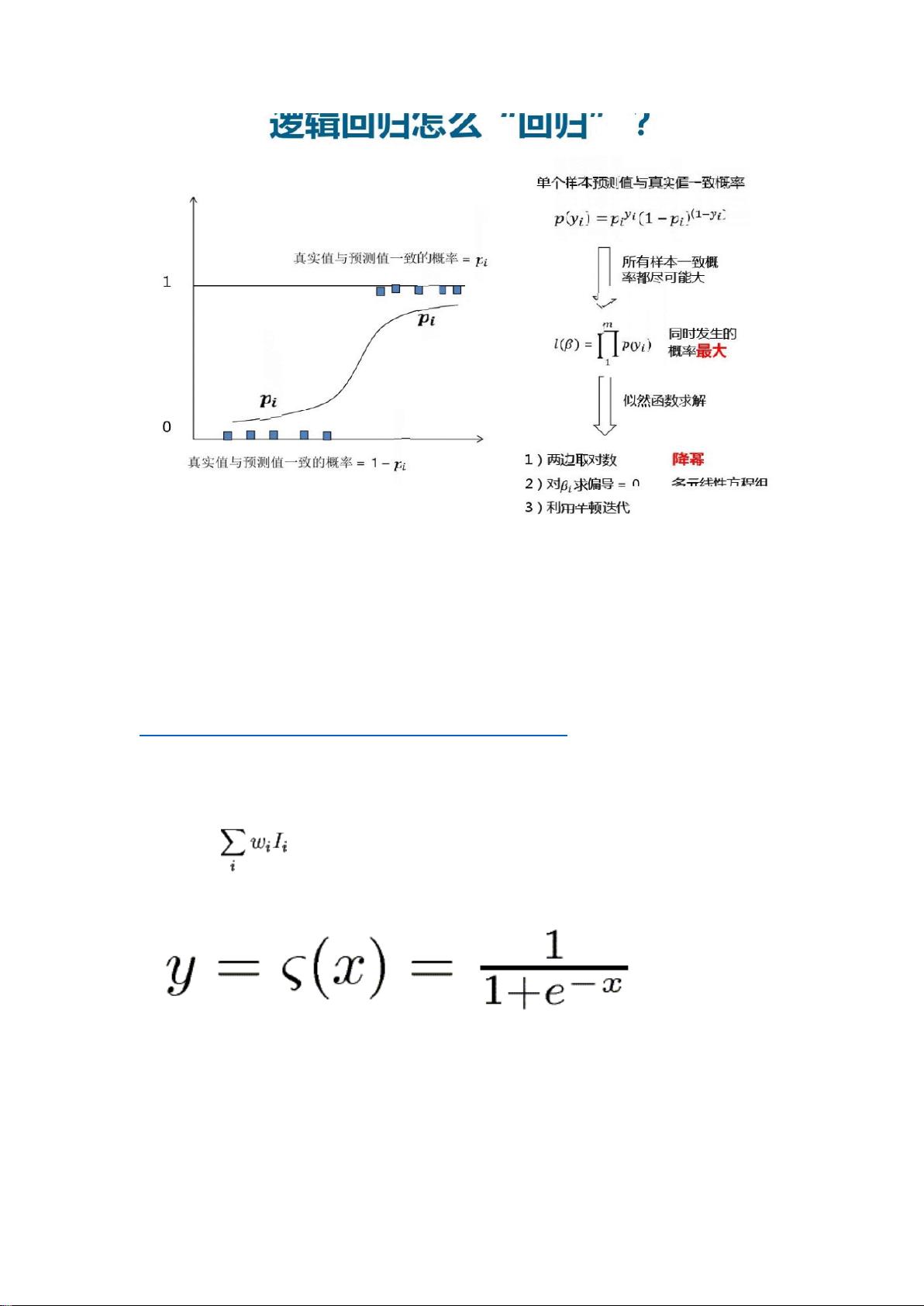
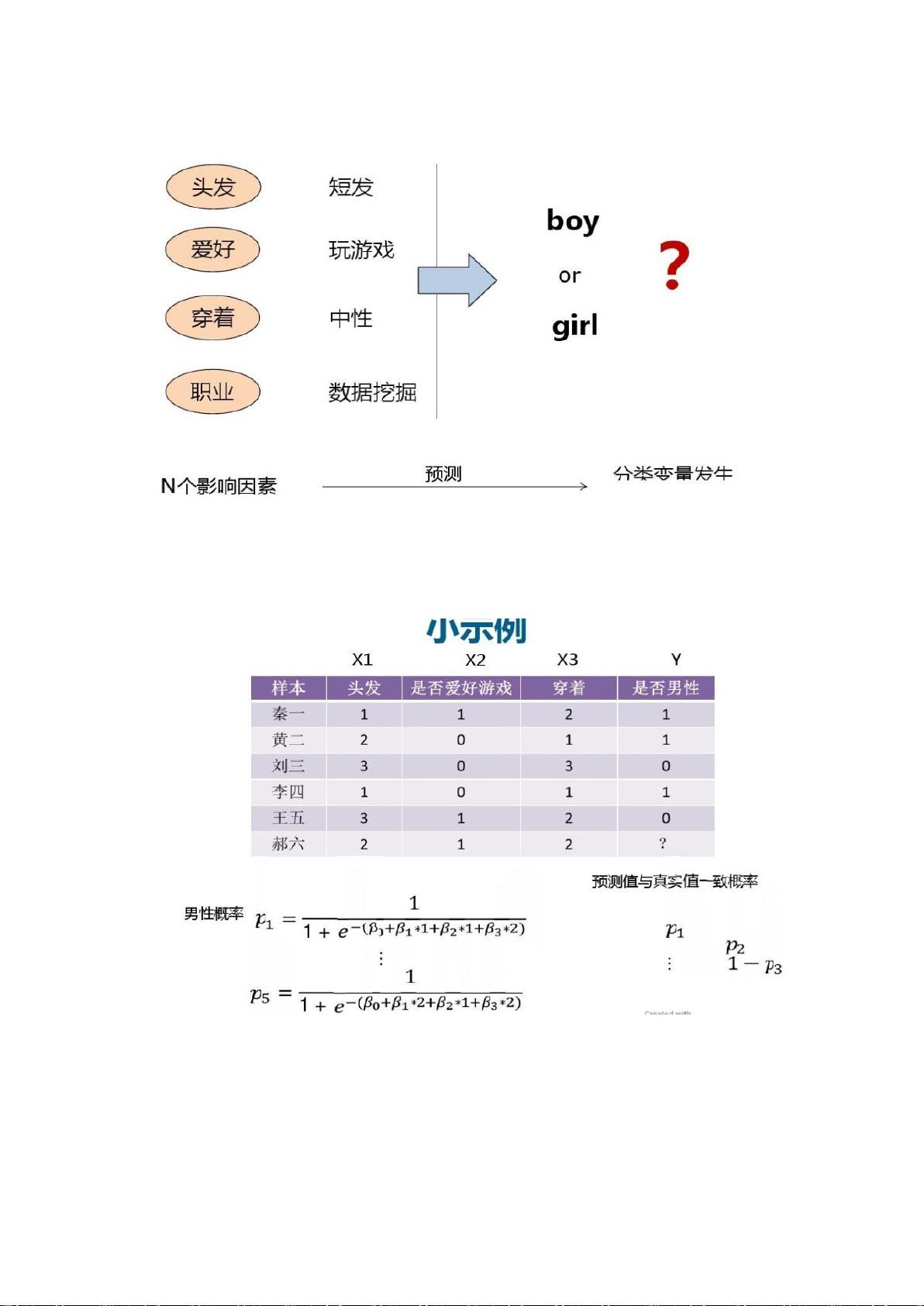
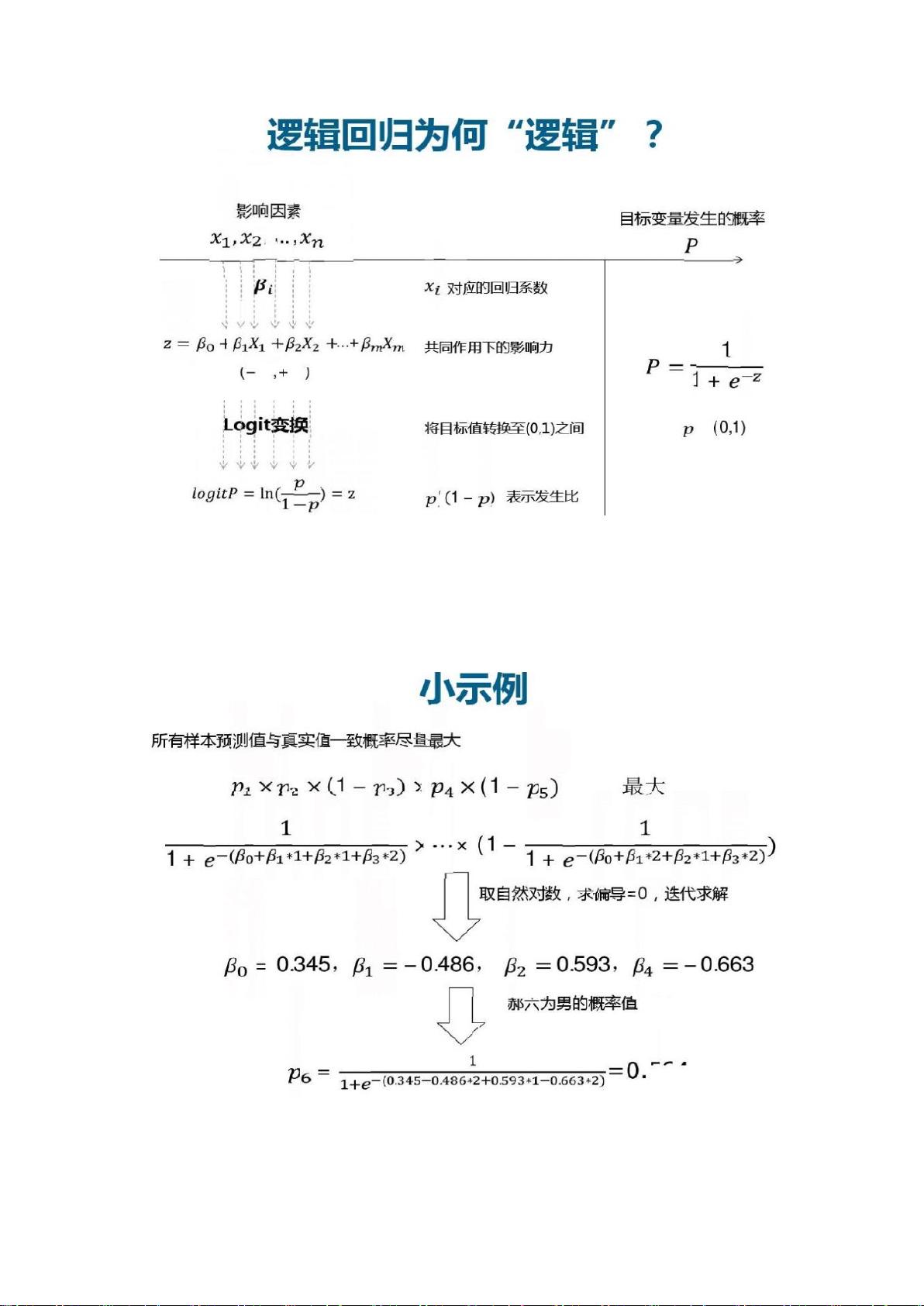
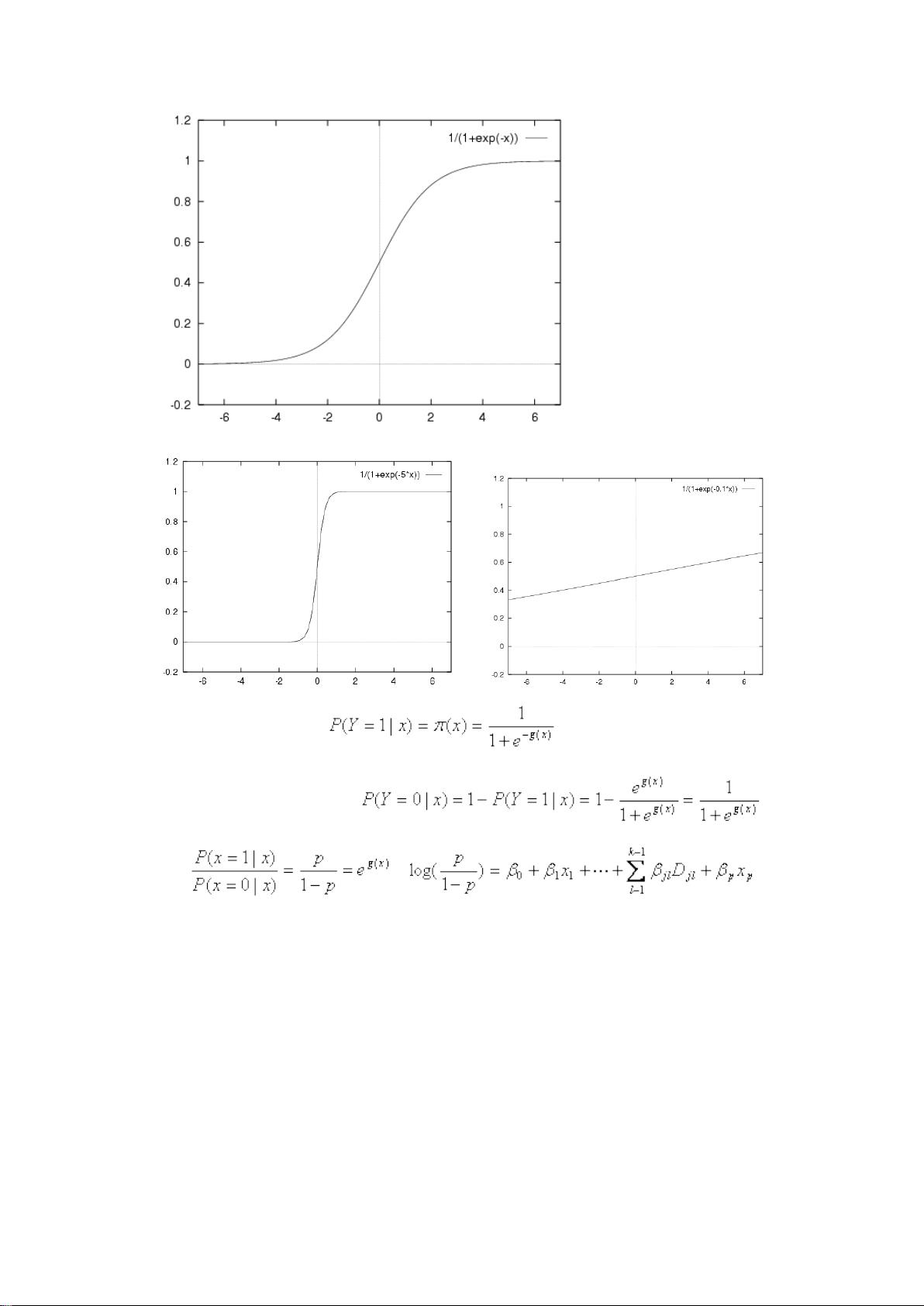
### 极大似然、S函数与逻辑回归学习笔记知识点详解 #### 1. 极大似然估计的基本思想及应用 **极大似然估计**是一种统计学中的参数估计方法，其基本思想是在已知观测数据的情况下寻找最有可能产生这些数据的参数值。这种方法的核心在于构造一个称为“似然函数”的函数，该函数描述了不同参数值产生已知数据的可能性大小。 - **基本思想**: 当我们有一组观测数据，并且知道这些数据是从某个分布中产生的，但不知道该分布的具体参数时，我们可以利用极大似然估计来找到最有可能产生这组数据的参数值。具体而言，就是选择那些使得观测数据发生的概率最大的参数值。 - **应用场景**: 在机器学习中，极大似然估计被广泛应用于各种模型的参数估计，如逻辑回归、朴素贝叶斯等。 #### 2. 逻辑回归与Sigmoid函数 **逻辑回归**是一种用于解决二分类问题的线性模型，它通过使用Sigmoid函数将线性回归的输出转换为概率值，进而预测样本属于某一类别的概率。 - **Sigmoid函数**: \(S(x) = \frac{1}{1 + e^{-x}}\)。该函数将实数域内的值映射到(0,1)区间内，特别适合用于表示概率。 - **特性**: 连续、光滑、严格单调递增；关于(0,0.5)中心对称；易于调整形状。 - **逻辑回归模型**: 逻辑回归模型通常形式为\(P(y=1|x;\theta) = S(\theta^T x)\)，其中\(\theta\)为模型参数，\(x\)为输入特征向量，\(P(y=1|x;\theta)\)表示给定\(x\)时\(y=1\)的概率。 #### 3. 极大似然估计在逻辑回归中的应用 **极大似然估计**用于确定逻辑回归模型的参数，即寻找最合适的\(\theta\)值，使得模型给出的预测概率与实际观测结果之间的对数似然函数达到最大。 - **似然函数**: 给定一组训练数据\((x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ..., (x^{(m)}, y^{(m)})\)，似然函数为\(L(\theta) = \prod_{i=1}^{m} [P(y^{(i)}|x^{(i)}; \theta)]^{y^{(i)}} [1 - P(y^{(i)}|x^{(i)}; \theta)]^{1-y^{(i)}}\)。 - **对数似然函数**: 为了简化计算，通常会使用对数似然函数\(l(\theta) = \sum_{i=1}^{m} [y^{(i)} \log P(y^{(i)}|x^{(i)}; \theta) + (1 - y^{(i)}) \log (1 - P(y^{(i)}|x^{(i)}; \theta))]\)。 #### 4. 参数估计方法 **参数估计**的目标是最优化似然函数或对数似然函数，常用的方法包括牛顿-拉斐森迭代法和梯度上升/下降法。 - **牛顿-拉斐森迭代法**: 这是一种基于泰勒展开的迭代方法，通过逐步逼近的方式找到函数的零点。在逻辑回归中，该方法可用于最大化对数似然函数，从而估计模型参数\(\theta\)。 - **梯度上升/下降法**: - **梯度上升法**: 目标是最小化损失函数，每次更新参数\(\theta\)时沿着梯度的方向移动。 - **梯度下降法**: 目标是最大化对数似然函数，每次更新参数\(\theta\)时沿着梯度的反方向移动。 - **向量化方法**: 通过矩阵运算替代传统的for循环，提高计算效率。 #### 5. 模型评估与优化 - **过拟合**: 当模型过于复杂，以至于在训练数据上表现很好但在新数据上表现不佳的现象。 - **显著性检验**: 用于评估模型参数的重要性。 - **变量选择**: 通过选择最相关的特征来构建更简洁有效的模型。 #### 6. 多分类问题 - **多分类器**(如Softmax Regression): 用于处理多于两个类别的分类问题，通过扩展逻辑回归模型实现。 #### 7. 概率论基础 - **概率密度函数**与**分布函数**的区别。 - **经典概率密度函数**: 包括二项分布、泊松分布、指数分布、正态分布等。 - **二项分布**: 描述重复试验中成功次数的概率分布。 - **泊松分布**: 用于描述单位时间内随机事件发生的次数。 - **指数分布**: 常用于描述等待时间的概率分布。 - **正态分布**: 最常见的连续概率分布之一，具有良好的统计性质。 #### 结语 以上内容详细阐述了极大似然估计、Sigmoid函数、逻辑回归及其在具体案例中的应用，同时介绍了几种常用的参数估计方法以及模型评估与优化的相关知识。希望这些知识点能够帮助读者更好地理解和掌握逻辑回归模型的核心概念和技术细节。