R语言主成分和因子分析数据降维技巧

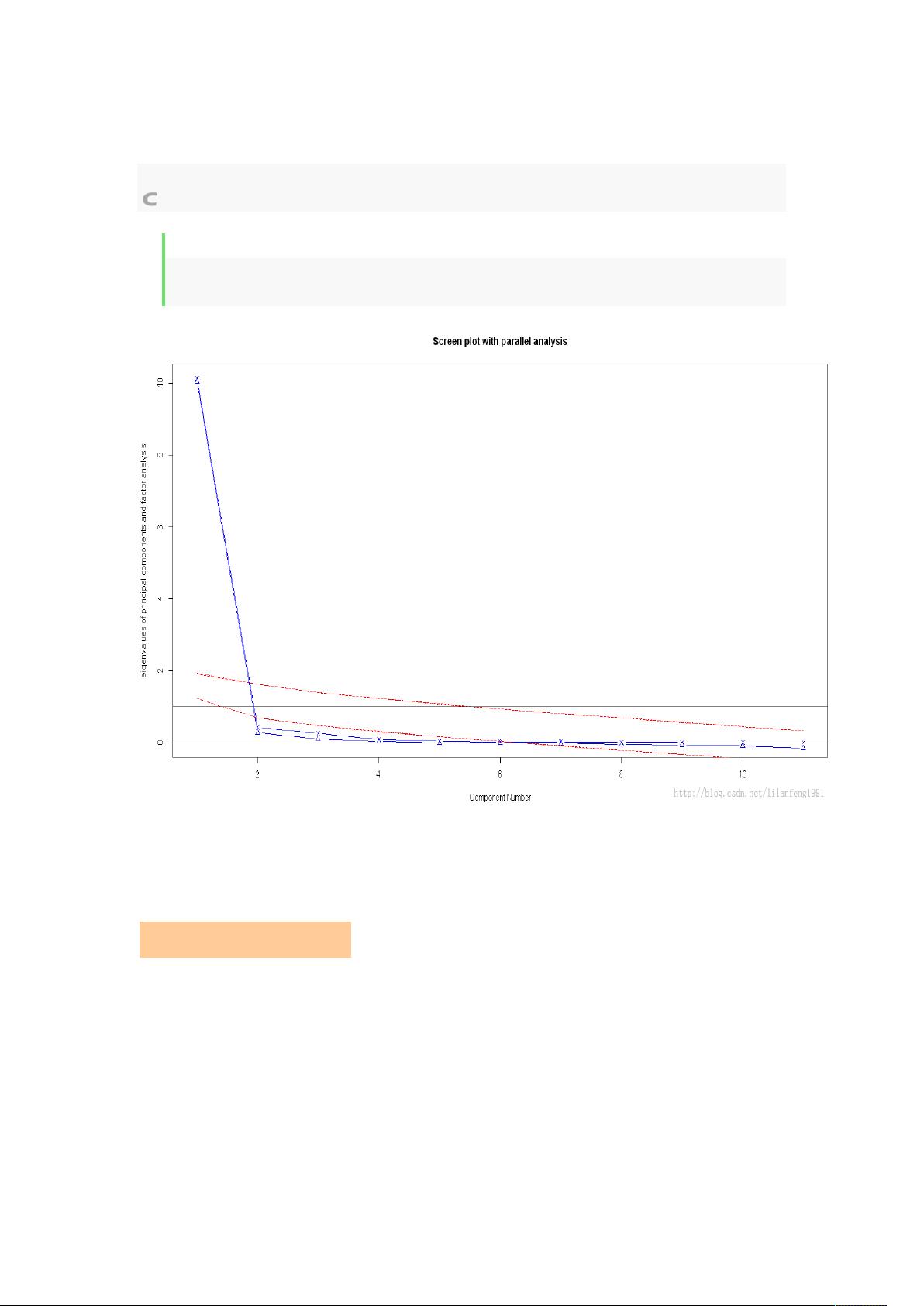
在数据分析领域，主成分分析（PCA）和因子分析（FA）是两种常用的数据降维技术，尤其在R语言中有着广泛的应用。这两种方法都是为了从高维数据中提取关键信息，减少数据复杂性，同时也帮助识别变量之间的潜在结构。 主成分分析（PCA）的核心目标是通过线性变换将一组可能存在相关性的变量转化为一组新的不相关的变量，即主成分。这些主成分是原始变量的线性组合，且每个主成分的方差解释度依次递减。PCA的目的是在尽可能保留原始数据信息的同时，减少数据的维度。例如，第一主成分是所有变量的加权组合，其解释的方差最大，而后续的主成分则依次降低，同时与前面的主成分保持正交关系。 在R中，可以使用`princomp()`函数执行PCA。但需要注意，PCA的结果通常需要进一步解读，包括确定主成分的数量。这可以通过多个准则完成，比如特征值、累计方差百分比或者通过平行分析等方法。Kaiser-Harris准则建议选取特征值大于1的主成分，而Cattell的碎石检验则依赖于特征值随主成分数变化的图形。`fa.parallel()`函数可以方便地进行平行分析，以辅助决定主成分的个数。 因子分析（FA）则更侧重于发现变量间的潜在结构，它假设原始数据可以由少数几个不可观测的因子解释。FA有多种估计方法，如主轴法、最小残差法、加权最小二乘法和最大似然法，这些方法可以在`fa()`函数中选择。R的`psych`包提供了丰富的因子分析工具，如`fa.parallel()`用于平行分析，`fa.diagram()`用于可视化因子载荷，以及`scree()`函数绘制碎石图来判断因子数量。 在进行FA时，分析流程与PCA类似，包括数据预处理、选择合适的因子分析模型、判断因子数目、旋转因子、解释结果和计算因子得分。选择因子数目同样可以通过特征值、碎石图和平行分析等方法。一旦确定因子数目，`factanal()`函数可以帮助执行因子分析。 在实际应用中，PCA和FA的选择取决于研究目的。PCA主要用于数据降维，保留主要的方差信息，而FA则更关注于揭示隐藏的结构，适用于探索性研究。两者都可以通过R语言中的相应函数高效实现，但理解其背后的统计原理和解读结果的方法至关重要，这样才能有效地运用到实际的数据分析项目中。