没有合适的资源?快使用搜索试试~ 我知道了~
Direct3D 中实现图元的鼠标
温馨提示
Direct3D 中实现图元的鼠标 看网上好多关于该文章的图片丢失,有幸找到个有图片的。
资源推荐
资源详情
资源评论

Direct3D
Direct3D
Direct3D
Direct3D
中实现图元的鼠标拾取
索引:
1 、什么是拾取,拾取能做什么?
2 、拾取操作的步骤和实现
2.1 . 变换并获得通过视点和屏幕上点击点的射线矢量( Dir )
2.1.1 确定鼠标选取点的屏幕坐标
2.1.2 得到 Dir 在观察坐标空间内的表示
2.1.3 转换 Dir 到世界坐标空间,并得到观察点在世界坐标系中的坐标
2.2 使用射线矢量对场景中的所有三角形图元求交,获得三角形索引值和重心坐标。
2.2.1 D3D 扩展函数实现求交
2.2.2 射线三角面相交的数学算法
2.2.3 拾取完成根据获得的中心坐标计算我们关心的常见量
3 、结束及声明
4 、参考文献
补充:重心坐标的概念
3D 交互图形应用程序中,常常要用鼠标去选择图形,其实现的机制基于鼠标拾取算法。本文主
要讲述如何在 D3D 中实现图元的鼠标拾取。为了讨论简单,本文假定读者理解 D3D 坐标变换流程 和
基本的图形学知识,如果阅读有困难请参考相关资料。
1
1
1
1
、什么是拾取,拾取能做什么?
首先,拾取操作指当我们在屏幕上用鼠标点击某个图元 , 应用程序能返回该图元的一个标志和某
些相关信息。有图形程序设计经验的人都知道,有这些信息就表示我们有了对该图元的控制权,我 们
可以删除,可以编辑,可以任意对待该图元,至于你到底想干什么,就是阁下自己的事了 ^_^ 。
2
2
2
2
、拾取操作的步骤和实现
拾取算法的思想很简单:得到鼠标点击处的屏幕坐标,通过投影矩阵和观察矩阵把该坐标转换 为
通过视点和鼠标点击点的一条射入场景的光线,该光线如果与场景模型的三角形相交(本文只处理 三
角形图元) ,则获取该相交三角形的信息。本文讲述的方法除可以得到三角形的一个索引号以外还可
以得到相交点的重心坐标。
从数学角度来看,我们只要得到射线的 方向矢量 和射线的 发 射点 ,我们就具备了判断射线与空间三 角
面是否相交的条件,本文主要讨论如何获得这些条件,并描述了射线 与 三角面相交判断算法和 D3D
的通常实现方法。
根据拾取操作的处理顺序,大概可以依次分为以下几个步骤
2.1
2.1
2.1
2.1
. 变换并获得通过视点和屏幕上点击点的射线矢量( Dir
Dir
Dir
Dir
)
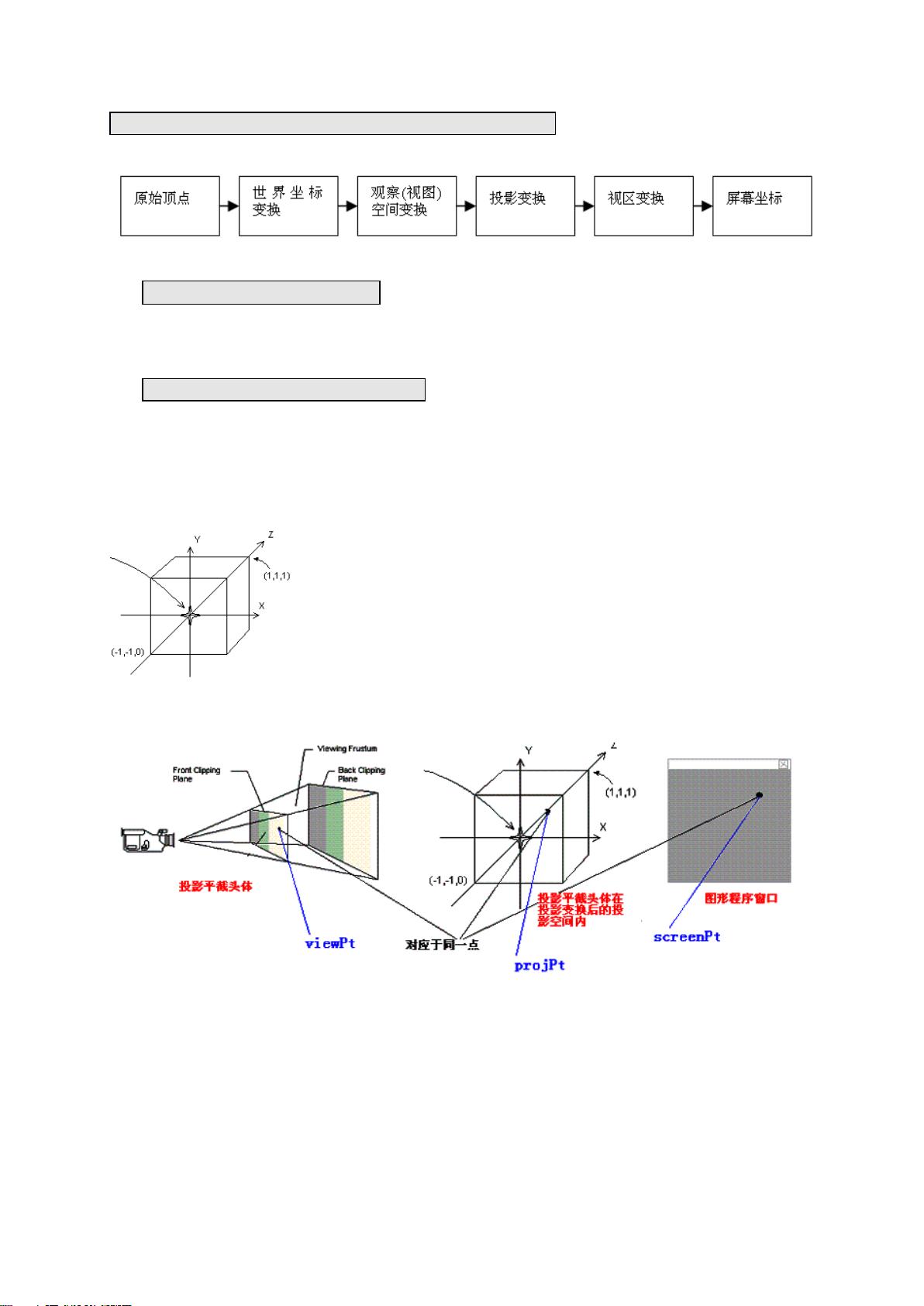
详细介绍之前,为了大家方便理解,我们要先简单说一下 d3d 坐标转换的大概流程,如下图 :
所以我们要通过一系列的反变换,得到我们关心的值在世界坐标中的表示。
2.1.1 确定鼠标选取点的屏幕坐标
这一步是非常简单的 Windows 给我们提供了 API 来完成屏幕坐标的获取,使用 GetCursorPos 获
得鼠标指针位置, 然后再利用 ScreenToClient 转换坐标到客户区坐标系 ( 以窗口视区左上角为坐标原
点,
单位为像素 ) ,设该坐标为( POINT screenPt
) 。
2.1.2 得到 Dir 在观察坐标空间内的表示
在观察坐标系中, Dir 是一条从观察坐标原点出发的射线,所以我们只需要再确定一个该射线经
过的点,就可以得到它在观察坐标系中的表示。假设我们要求的射线上的另外一点为该射线与透视 投
影平截头体近剪切面的交点,针对最普遍的透视投影而言,透视投影平截头体经投影变换后,变成 一
个 1/2 立方体(请允许我这么叫 ^_^ ,因为它的大小为一个正方体的一半, x,y 方向边长为 2
,
z 方向 为
1 )如图:
投影坐标系以近剪切面中心为坐标原点,该立方体从 z 轴负向看过去与图形程序视区相对应,最终 近
剪切面(前剪切面)上一点与屏幕坐标之间的对应关系如下图所示:
根据比例关系, screenPt 与投影空间上的点 projPt 之间的关系为
假设图形程序窗口的宽为 screenWidth, 高为 screenHeight,
projPt.x = (screenPt.x-screenWidth/2)/screenWidth*2; (公式 1 )
projPt.y = (screenPt.y-screenHeight/2)/screenHeight*2; (公式 2 )
projPt.z =0; (实际该值可任意取,不影响最终结果。为了处理简单,我们取改值为 0 ,表示该点
取在近剪切面上)
得到 projPt 后,我们需要做的是把该点坐标从投影空间转换到观察空间 (view space),
根据透视投影的定义,可假设点 (projPt.x , projPt.y , projPt.z)
剩余7页未读,继续阅读
资源评论

 madchemist2015-07-23很好的教程!谢谢
madchemist2015-07-23很好的教程!谢谢
zyq5945
- 粉丝: 604
- 资源: 19
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- matlab平台的的PCB板缺陷检测.zip
- matlab平台的的SVM方法的水果识别分类.zip
- matlab平台的的答题纸答题卡识别.zip
- matlab平台的的病虫害检测系统.zip
- 基于python的多传感器数据融合故障诊断程序,三条分支
- sgp4与sdp4模型文档+一个SGP4的开源实现
- matlab平台的的车道线标定.zip
- matlab平台的的人脸+指纹融合系统.zip
- matlab平台的的路牌交通牌照识别.zip
- JAVA多线程示例代码
- matlab平台的的人脸门禁预警.zip
- matlab平台的的手写汉字识别.zip
- matlab平台的的人脸识别设计.zip
- matlab平台的的视频图像去雾.zip
- matlab平台的的手写字符识别.zip
- matlab平台的的小波变换dwt数字水印.zip
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功