没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

调和点列中的定比点差法
【微点综述】
定比点差在处理三点共线、相交弦、定点定值、比例问题、调和点列等问题均具有优势,本文介绍定比点差法在调
和点列中的应用.
一、调和定比分点
若 AM
= λMB
且 AN
=-λNB
,则称 M ,N 调和分割 A,B,根据定义,那么 A,B 也调和分割 M ,N (其中 M
在线段 AB 内,称为内分点,N 在线段 AB 外,称为外分点).
二、调和定比分点的性质
【性质1】在椭圆或双曲线
x
2
a
2
±
y
2
b
2
= 1 a > 0,b > 0
中,设 A,B 为椭圆或双曲线上的两点.若存在 M ,N 调
和分割 A,B,即满足 AM
= λMB
,AN
=-λNB
,则一定有
x
M
x
N
a
2
±
y
M
y
N
b
2
= 1.
证明:由已知点 A x
1
,y
1
,B x
2
,y
2
在椭圆或双曲线
x
2
a
2
±
y
2
b
2
= 1 a > 0,b > 0
上,设 M x
M
,y
M
,
N x
N
,y
N
.首先 AM
= λMB
,则由定比分点坐标公式可得
x
M
=
x
1
+λx
2
1 + λ
,
y
M
=
y
1
+λy
2
1 + λ
,
又 AN
=-λNB
,则由定比分点坐标公式可得
x
N
=
x
1
-λx
2
1 - λ
,
y
N
=
y
1
-λy
2
1 - λ
,
当 λ ≠±1 时,将 A x
1
,y
1
,B x
2
,y
2
代入曲线,有
x
2
1
a
2
±
y
2
1
b
2
= 1 ①
x
2
2
a
2
±
y
2
2
b
2
= 1 ②
,
② × λ
2
得到
λ
2
x
2
2
a
2
±
λ
2
y
2
2
b
2
= λ
2
③
③和①作差整理可得:
x
1
+λx
2
x
1
-λx
2
a
2
1 + λ
1 - λ
±
y
1
+λy
2
y
1
-λy
2
b
2
1 + λ
1 - λ
= 1,将前式代入整理得
x
M
x
N
a
2
±
y
M
y
N
b
2
= 1.
【性质2】在抛物线 y
2
= 2px 中,设 A,B 为抛物线上的两点.若存在 M ,N 调和分割 A,B ,即满足 AM
=
λMB
,AN
=-λNB
,则一定有 y
P
y
Q
= p x
P
+x
Q
.
证明:设 A x
1
,y
1
,B x
2
,y
2
,由 AM
= λMB
,得 M
x
1
+λx
2
1 + λ
,
y
1
+λy
2
1 + λ
,
由 AN
=-λNB
,得 N
x
1
-λx
2
1 - λ
,
y
1
-λy
2
1 - λ
,
又
y
1
2
= 2px
1
①
λ
2
y
2
2
= 2λ
2
px
2
②
,① - ②得:y
1
2
-λ
2
y
2
2
= p x
1
+x
1
-λ
2
x
2
-λ
2
x
2
,
即 y
1
+λy
2
y
1
-λy
2
= p x
1
+λx
2
+x
1
-λx
2
+λx
1
-λ
2
x
2
-λx
1
-λ
2
x
2
,
y
1
+λy
2
y
1
-λy
2
1 + λ
1 - λ
=
p(x
1
+λx
2
) 1 - λ
1 - λ
1 + λ
+
p x
1
-λx
2
1 + λ
1 - λ
1 + λ
,∴ y
P
y
Q
= p x
P
+x
Q
.
在椭圆、双曲线或抛物线中,设 A x
1
,y
1
定比点差的原理谜题解开,就是两个互相调和的定比分点坐标满足圆锥曲线的特征方程.
【性质3】
定比点差转换定理:
,B x
2
,y
2
为椭圆或双曲线上的两点.若存在 P,Q 两点,满足
AP
= λPB
,AQ
=-λQB
,则一定有
x
1
=
x
P
+x
Q
2
+
x
P
-x
Q
2
⋅ λ,
x
2
=
x
P
+x
Q
2
+
x
P
-x
Q
2λ
.
(重点中的重点!!!)
证明:
x
P
x
Q
a
2
±
y
P
y
Q
b
2
= 1 ⇒
x
1
+λx
2
1 + λ
= x
P
,
x
1
-λx
2
1 - λ
= x
Q
⇒
x
1
+λx
2
= 1 + λ
x
P
,
x
1
-λx
2
= 1 + λ
x
Q
⇒
x
1
=
x
P
+x
Q
2
+
x
P
-x
Q
2
⋅ λ,
x
2
=
x
P
+x
Q
2
+
x
P
-x
Q
2λ
.
三、
定比点差法在调和点列中的应用
例1.
已知椭圆 C:
x
2
4
+
y
2
2
= 1,过点 P 4,1
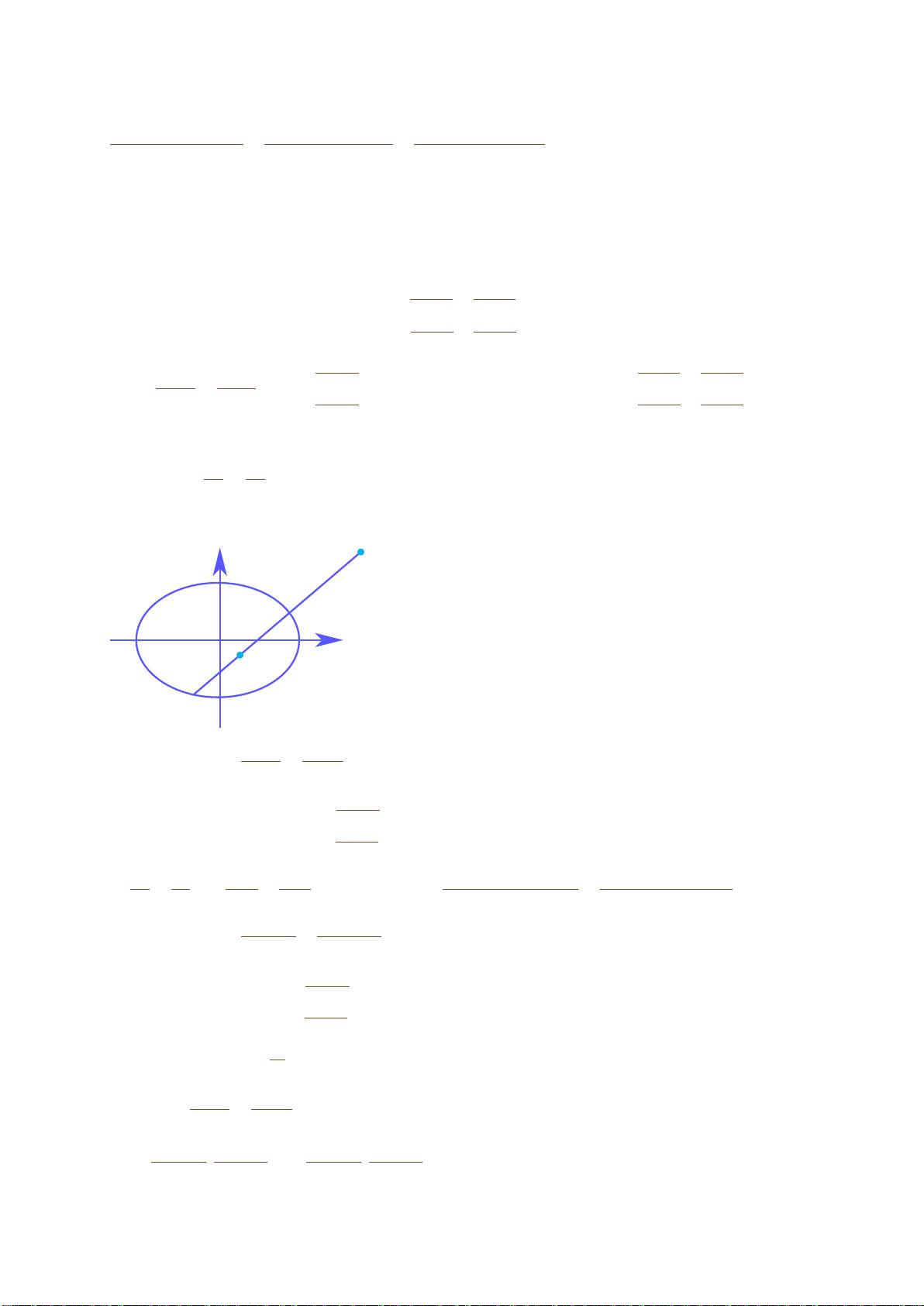
的动直线 l 交椭圆 C 于 A,B 两点,在线段 AB 上取点 Q 满足
AP
QB
= AQ
PB
,求证:点 Q 在某条定直线上.
A
B
O
P
Q
x
y
【解析】解法一:设
AP
PB
=
AQ
BQ
= λ λ ≠ 1
,即 AP
= λPB
,AQ
=-λQB
,设 A x
1
,y
1
,B x
2
,y
2
,
Q x,y
,由于 AP
= λPB
,
4 =
x
1
+λx
2
1 + λ
⋅⋅⋅ ①
1 =
y
1
+λy
2
1 + λ
⋅⋅⋅ ②
,
又
x
2
1
4
+
y
2
1
2
= 1,
λ
2
x
2
2
4
+
λ
2
y
2
2
2
= λ
2
,两式相减得
x
1
+λx
2
x
1
-λx
2
4
+
y
1
+λy
2
y
1
-λy
2
2
= 1 - λ
2
③
①②式代入③式,
x
1
-λx
2
1 - λ
+
y
1
-λy
2
2 1 - λ
= 1 ④
又由于 AQ
=-λQB
,
x =
x
1
-λx
2
1 - λ
⋅⋅⋅ ⑤
y =
y
1
-λy
2
1 - λ
⋅⋅⋅ ⑥
,
⑤⑥式代入④式,x +
1
2
y = 1,即点 Q 在定直线 2x + y - 2 = 0 上.
解法二:设
AP
PB
=
AQ
BQ
= λ λ ≠ 1
,即 AP
= λPB
,AQ
=-λQB
,设 A x
1
,y
1
,B x
2
,y
2
,Q x
0
,y
0
,
则 P
x
1
-λx
2
1 - λ
,
y
1
-λy
2
1 - λ
,Q
x
1
+λx
2
1 + λ
,
y
1
+λy
2
1 + λ
,
于是有
x
1
-λx
2
1 - λ
= 4,
y
1
-λy
2
1 - λ
= 1,
x
1
+λx
2
1 + λ
= x
0
,
y
1
+λy
2
1 + λ
= y
0
,
由点 A,B 在椭圆上,则
x
2
1
+2y
2
1
= 4,
λ
2
x
2
1
+2λ
2
y
2
1
= 4λ
2
,
于是有
x
1
+λx
2
1 + λ
⋅
x
1
-λx
2
1 - λ
+ 2 ⋅
y
1
+λy
2
1 + λ
⋅
y
1
-λy
2
1 - λ
= 4,即 4x
0
+2y
0
= 4,故点 Q 在定直线 2x + y - 2 = 0 上.
【评注】共线的四点成两组等比例线段,于是设 AP
= λPB
,AQ
=-λQB
,自然想到定比点差法,非常巧
妙地得到结论,体现出定比点差法比其他方法的优越性.
例2. 已知 F
1
、F
2
分别为椭圆 C
1
:
y
2
a
2
+
x
2
b
2
= 1(a > b > 0) 的上、下焦点,其中 F
1
也是抛物线 C
2
:x
2
= 4y 的焦
点,点 M 是 C
1
与 C
2
在第二象限的交点,且 |MF
1
| =
5
3
.
O
x
y
M
F
1
F
2
(1) 求椭圆 C
1
的方程;
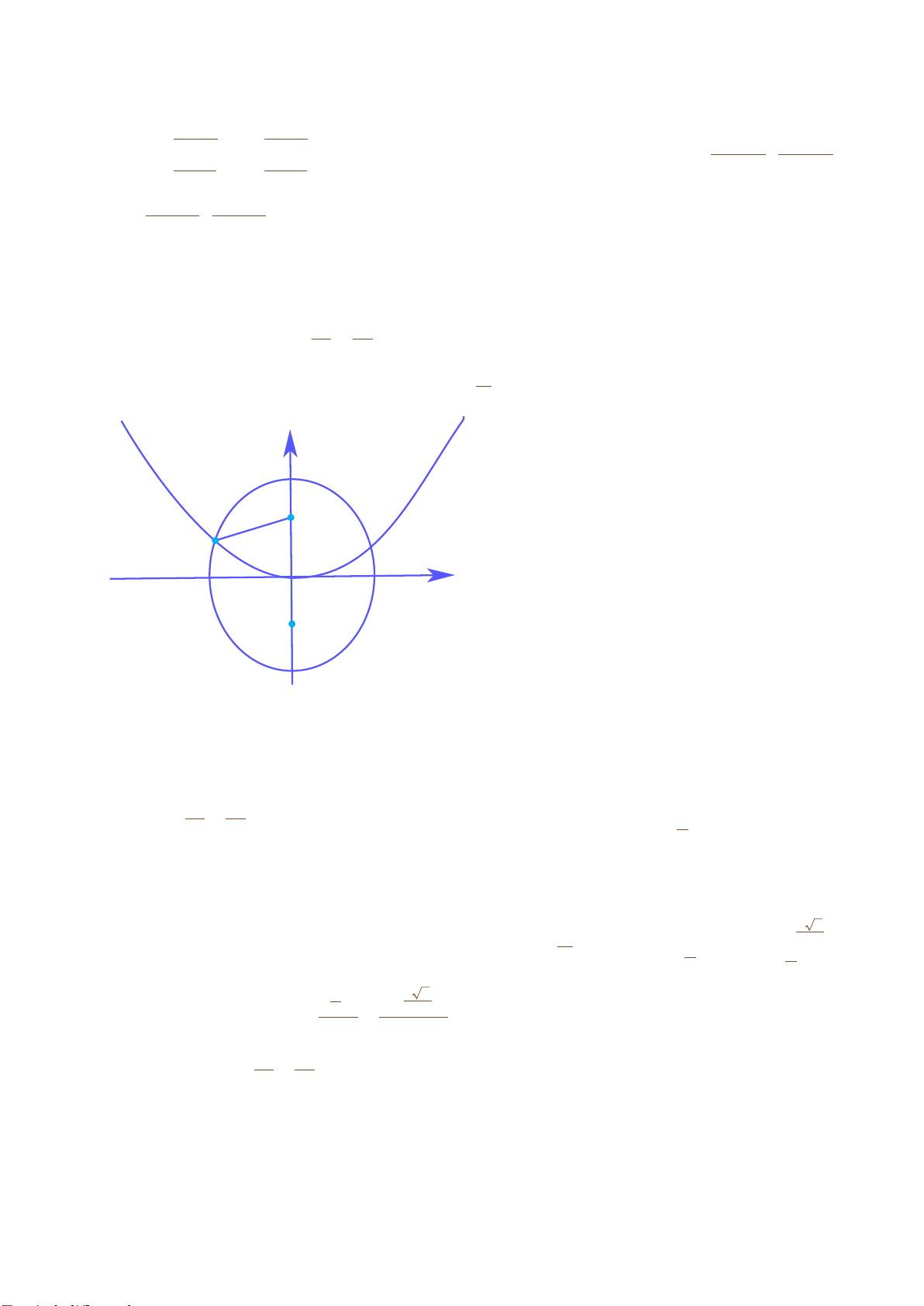
(2) 已知点 P(1,3) 和圆 O:x
2
+y
2
= b
2
,过点 P 的动直线 l 与圆 O 相交于不同的两点 A,B,在线段 AB 上
取一点 Q,满足:AP
=-λPB
,AQ
= λQB
,(λ ≠ 0 且 λ ≠±1).求证:点 Q 总在某定直线上.
【答案】(1)
y
2
4
+
x
2
3
= 1;(2)x + 3y = 3 析】(1) 设 M x
0
,y
0
,由已知得
x
0
2
= 4y
0
y
0
+1 =
5
3
,可求得点 M 的坐标,
代入椭圆的方程中可求得 a,b,c,可得椭圆 C
1
的方程;(2) 由向量的坐标运算和向量相等的条件,以及
点在圆上可得出点 Q 所在的直线.
【解析】(1) 设 M x
0
,y
0
,因为点 M 在抛物线 C
2
上,且 |MF
1
| =
5
3
,所以
x
0
2
= 4y
0
y
0
+1 =
5
3
,解得
x
0
=-
2 6
3
y
0
=
2
3
,
又点 M 在抛物线 C
1
上,所以
2
3
2
a
2
+
-
2 6
3
2
b
2
= 1,且 c = 1,即 b
2
= a
2
-1,解得 a
2
= 4,b
2
= 3,
所以椭圆 C
1
的方程
y
2
4
+
x
2
3
= 1;
(2) 设 A x
1
,y
1
,B x
2
,y
2
,Q x,y
,因为 AP
=-λPB
,所以 1 - x
1
,3 - y
1
=-λ x
2
-1,y
2
-3
,即有
x
1
-λx
2
= 1 - λ, 1
y
1
-λy
2
= 3 1 - λ
, 2
,

又 AQ
= λQB
,所以 x - x
1
,y - y
1
= λ x
2
-x,y
2
-y
,即有
x
1
+λx
2
= x 1 + λ
, 3
y
1
+λy
2
= y 1 + λ
, 4
,
所以 1
× 3
+ 2
× 4
得:x
1
2
+y
1
2
-λ
2
x
2
2
+y
2
2
= x + 3y
1 - λ
2
,
又点 A、B 在圆 x
2
+y
2
= 3 上,所以 x
1
2
+y
1
2
= 3,x
2
2
+y
2
2
= 3,又 λ ≠±1,所以 x + 3y = 3,
故点 Q 总在直线 x + 3y = 3 上.
O
P
Q
A
B
x
y
【评注】本题考查椭圆和抛物线的简单几何性质,以及直线与圆的交点问题,属于较难题.
例3. 在平面直角坐标系 xOy 中,已知椭圆 C :
x
2
a
2
+
y
2
b
2
= 1 a > b > 0
的离心率为
1
2
,以椭圆上的一点和
长轴的两个端点为顶点的三角形面积最大值为 2 3.
(1) 求 a,b 的值;
(2) 当过点 P 6,0
的动直线 l 与椭圆 C 交于不同的点 A,B 时,在线段 AB 上取点 Q,使得 AP
⋅ BQ
+
AQ
⋅ BP
= 0,问点 Q 是否总在某条定直线上?若是,求出该直线方程,若不是,说明理由.
【答案】(1)a = 2,b = 3;(2) 直线 Q 恒在定直线 x =
2
3
上析】(1) 利用椭圆 a,b,c 关系、离心率和三角
形面积可构造方程求得结果;
(2) 根据四点的位置关系可知
AP
AQ
=
BP
BQ
,由此可得 Q x
0
,y
0
中 y
0
=
2y
1
y
2
y
1
+y
2
,将直线 AB 方程代入
椭圆方程,得到韦达定理形式,整理可求得 y
0
,代入直线方程可知 x
0
=
3
2
恒成立,由此可确定结论.
【解析】(1) 以椭圆上的一点和长轴的两个端点为顶点的三角形面积最大时,三角形另一顶点为椭圆短
轴的端点,∴
a
2
= b
2
+c
2
e =
c
a
=
1
2
1
2
× 2a × b = ab = 2 3
,解得:a = 2,b = 3.
(2) 设 A x
1
,y
1
,B x
2
,y
2
,Q x
0
,y
0
,AP
⋅ BQ
=- AP
⋅ BQ
,AQ
⋅ BP
= AQ
⋅ BP
,
∴- AP
⋅ BQ
+ AQ
⋅ BP
= 0,即
AP
AQ
=
BP
BQ
,即
y
1
-0
y
1
-y
0
=
y
2
y
0
-y
2
,整理可得:y
0
=
2y
1
y
2
y
1
+y
2
,
剩余15页未读,继续阅读
资源评论

小鸭文库
- 粉丝: 196
- 资源: 5900
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 处理定时器和消息的队列.7z
- 基于netty3.5的游戏服务器端框架 消息封装,编解码结构提供扩展,请求消息队列处理,基于protobuf的实例已经完成.7z
- 一个服务器处理框架,包括 协议处理,消息处理,持久层数据处理.7z
- matlab实现粒子群算法综合线阵低副瓣方向图设计-粒子群算法-天线阵列-PSO算法-matlab
- 动态规划算法详解及应用实例分析
- fscan一款内网资产排查工具提高工作效率
- 800高压脱泡机.STEP全套设计资料100%好用.zip
- 动态规划算法详解及Python代码实现
- 50kg双向单立柱堆垛机step全套设计资料100%好用.zip
- BBR12包装机卷包机热熔编带机sw12可编辑+cad全套设计资料100%好用.zip
- SQLAlchemy 基础用法完整示例
- X射线平板探测器架车step全套设计资料100%好用.zip
- TE-桁架机械手sw12全套设计资料100%好用.zip
- Z2021-4-顶升移栽机sw18可编辑全套设计资料100%好用.zip
- 2024注册测绘师《综合能力》讲义-第3章-工程测量(3)城乡规划与建筑工程测量.pdf
- 点胶贴合机step全套设计资料100%好用.zip
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功