直接转矩控制外文资料资源-CSDN文库

5星 · 超过95%的资源需积分: 10 147 浏览量 2012-12-03 23:09:19 上传评论收藏 1.03MB PDF 举报

直接转矩控制（Direct Torque Control，简称DTC）是一种应用于交流电机驱动系统中的控制策略，尤其在永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）的控制中表现突出。DTC的核心优势在于其高动态响应能力，能够实现快速、精确的扭矩调节。与传统的矢量控制技术相比，DTC不依赖于复杂的数学模型和坐标变换，而是通过直接检测和控制电机的磁通和扭矩来实现目标。 ### 直接转矩控制的关键概念 #### 1. **磁通和扭矩的直接控制** 在DTC中，电机的磁通和扭矩是直接被测量和控制的参数，而非像矢量控制那样通过电流的间接控制。这种直接控制方式简化了控制系统的设计，同时提高了系统的响应速度。 #### 2. **滞环控制器的应用** DTC采用滞环控制器（Hysteresis Controller）来调节电机的磁通和扭矩。滞环控制器基于预设的滞环带宽（Hysteresis Bands），当实际值与参考值之间的偏差超过这个带宽时，控制器会采取行动，改变逆变器的开关状态，从而调整电机的运行状态。 #### 3. **开关频率的控制** 逆变器的开关频率对电机的效率和电磁兼容性有着直接影响。在DTC中，开关频率主要由磁通和扭矩控制器的输出开关计数决定。随着运行点的变化，固定滞环带宽下的开关频率也会随之变化。然而，通过适应性地调整滞环带宽，可以保持开关频率的恒定，这对于优化电机性能至关重要。 ### 优化滞环带宽的方法为了实现最优控制，需要从众多可能的磁通和扭矩滞环带宽组合中选择最合适的那一个。文献提出了一种基于最小电流谐波失真（Total Harmonic Distortion，THD）的准则来选择滞环带宽。这种方法考虑了在特定开关频率下，如何使电机电流的谐波失真最小化，从而优化电机的运行效率和电磁兼容性。 ### 分析过程与验证文献中提供了一套分析程序，用于计算PMSM在DTC模式下的最优滞环带宽。这一理论结果通过仿真研究得到了验证，并通过详细的实验测试进行了确认。为了防止计算延迟对控制性能的影响，文献采用了基于现场可编程门阵列（Field-Programmable Gate Array，FPGA）的控制平台进行实施，确保了控制的实时性和准确性。 ### 结论直接转矩控制作为一种先进的电机控制策略，已经在工业应用中展现出其独特的优势，特别是在追求高动态响应和简化控制系统设计的场景中。通过对滞环带宽的优化选择，不仅可以提高电机的效率和性能，还能减少电磁干扰，提升系统的整体可靠性。未来，随着硬件技术的进步和算法的不断优化，DTC在电机控制领域的应用将更加广泛，为工业自动化和智能制造带来更大的潜力。

资源推荐

资源详情

资源评论

IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 60, NO. 3, MARCH 2013 885

Analytical and Ofﬂine Approach to Select Optimal

Hysteresis Bands of DTC for PMSM

Shashidhar Mathapati and Joachim Böcker, Member, IEEE

Abstract—The switching frequency of an inverter under direct

torque control is mainly decided by the ﬂux- and torque-controller

output switching counts. It is known that, with ﬁxed hysteresis

bands, the switching frequency varies as the operating point

changes. It is possible, however, to keep the switching frequency

constant by the adaptation of hysteresis bands. The switching

frequency is a function of both torque and ﬂux bands. Different

combinations of ﬂux and torque bands can be used to achieve

a desired switching frequency. However, for optimal control, one

among the many available combinations has to be chosen. In

this contribution, it is proposed to select the hysteresis bands

based on the criterion of the minimum harmonic distortion in the

motor currents for the required switching frequency. An analytical

procedure is presented to calculate these optimal bands for the

permanent-magnet synchronous motor. The analytical results

were cross checked with simulation studies and validated by

detailed experimentation. In order not to degrade the control

performance by computational delay, a ﬁeld-programmable-gate-

array-based control platform is being used for implementation.

Index Terms —Direct torque control (DTC), ﬁeld-

programmable gate array (FPGA), optimal control, permanent-

magnet synchronous motor (PMSM), total harmonic distortion

(THD).

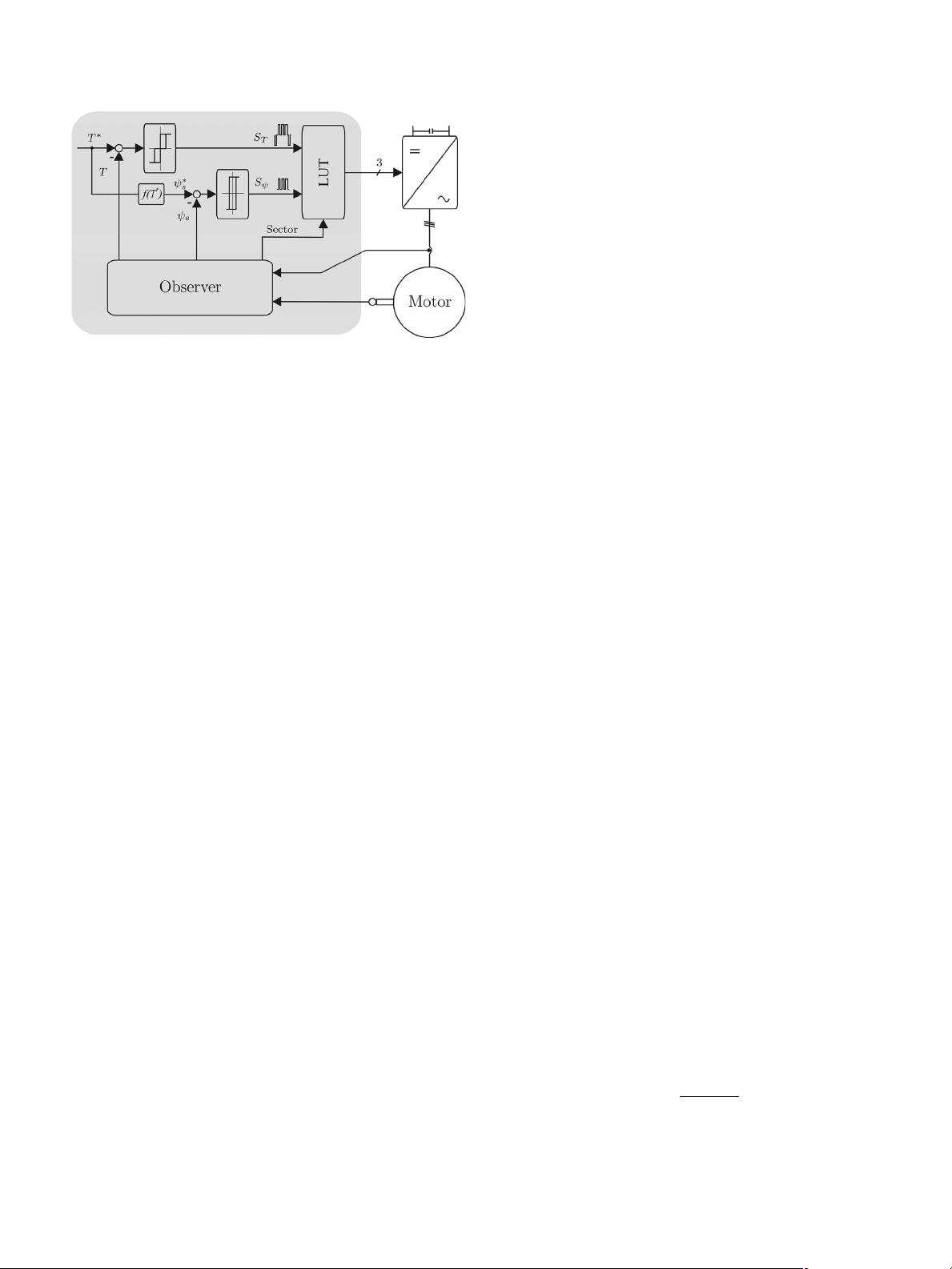
I. INTRODUCTION

HE direct torque control (DTC) [1] of ac motor drives

has been known in the drives industry for more than two

decades. Another control similar to the DTC is the direct self-

control (DSC) [2]. Both inventions had been published around

the same time in the mid-80s. These controls are known for their

highest control dynamics of torque regulation, and both of them

utilize hysteresis controllers to regulate the torque and the ﬂux

of the motor. The main difference exists in the trajectory of the

ﬂux control; the DSC guides the ﬂux vector along a hexagonal

trajectory (or 18 corners), whereas with the DTC, it is circular.

The application of the DSC is mainly seen in traction drives

because it can cope with rather low switching frequencies. The

DTC is utilized with low and medium power drives due to its

better total harmonic distortion (THD) and higher switching

frequency [3], [4]. Our discussion in this paper is limited only

to the DTC.

The DTC however has the i nherent problem of varying

switching frequency with constant hysteresis bands, which is

undesired for some applications. In order to improve this,

Manuscript received July 22, 2010; revised November 11, 2010 and

February 23, 2011; accepted September 22, 2011. Date of publication

February 29, 2012; date of current version October 16, 2012.

S. Mathapati is with the Delta India Electronics, Bangalore 560068, India

(e-mail: Mathapati.Shashidhar@googlemail.com).

J. Böcker is with the University of Paderborn, 33098 Paderborn, Germany

(e-mail: boecker@lea.upb.de).

Digital Object Identiﬁer 10.1109/TIE.2012.2189530

researchers have worked on different approaches. Contributions

[5] and [6] present a similar control s tructure, which had the

similar concept for torque control as in [1] and [2] but combined

with space-vector modulation (SVM). That indeed ensures the

constant switching frequency; however, the inherent robustness

and dynamics of the original DTC or DSC is lost with this ap-

proach. Extensive research has been seen in this direction; a de-

tailed survey on the DTC for induction machines can be found

in [7]. The research on the SVM-DTC of the permanent-magnet

synchronous motor (PMSM) is also intensively covered; some

of the recent references can be found in [8] and [9]. In [10]

and [11], some additional modiﬁcations of the basic DTC are

proposed to improve the switching frequency performance.

Very few publications worked on detailed analytical approaches

to analyze the DTC. In [12], an evaluation of the switching fre-

quency as a function of the hysteresis bands is given with a fo-

cus on the reduction of iron loss due to the higher ﬂux ripple. A

similar analysis is also presented in [13], where analytical cal-

culations of the ﬂux- and torque-controller switching are dealt

to evaluate the switching frequency. Both publications [12] and

[13] state that the switching frequency is not linearly related

to the THD and suggest that the ﬂux-controller band should be

small in comparison with the torque-controller band. Similarly,

a prediction technique is employed to improve the conventional

DTC’s torque and ﬂux ripple performance in [14] and [15]. In

spite of many such developments in the DTC, they have not

been able to make a signiﬁcant impact in capturing the market

of standard and servodrives. In fact, this is still dominated by

pulsewidth-modulation ( PWM) controls; the reasons lie in their

lower THD and the constant switching frequency of the inverter.

None of the publications from the literature survey has

proposed a strategy to select the hysteresis bands in order

to keep the switching frequency constant and/or to aim for

the optimal THD design. In this paper, the main focus is to

present a completely analytical and ofﬂine approach to evaluate

the optimal hysteresis bands, which ensure constant switching

frequency for the whole operating region of the drive. The

criterion for the selection of the hysteresis bands is based on

the minimum harmonics in the motor currents. In the course

of the proposed method’s evaluation procedure, comparisons

with simulation results are given at every step. After the ofﬂine

evaluation of the optimal hysteresis bands, experiments are

carried out for the validation.

It is well known that the performance of the hysteresis

controllers depends very much on the computational delay

or the dead time of the control. In order to ensure that the

control realization behaves very close to the continuous-time

performance, a ﬁeld-programmable gate array (FPGA) is used

886 IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 60, NO. 3, MARCH 2013

Fig. 1. Block diagram of the DTC.

for control implementation. As the analysis of continuous-time

systems is much simpler compared with sampled systems, this

circumstance also provides a greater ﬂexibility for the control

behavior analysis.

FPGA is not new for drives industry, they are known in

this ﬁeld for more than a decade, and very recent utilization

can be seen in [16]–[18]. A decade ago, their application was

limited to few custom drives due to their high cost and lack of

development tools. In the last few years, the cost of the FPGA

logic has drastically reduced and is still reducing. Advanced

development tools are available from the FPGA producers and

from third parties. Some of these tools can be also used in

conjunction or with the MATLAB–Simulink platform [19],

[20], which makes the development process faster. Some of the

development tools from FPGA manufacturers are available for

free, which are adequate for our purposes [21], [22].

This paper is organized as follows: In Section II, the an-

alytical evaluation of the torque- and ﬂux-controller output

frequencies, the inverter switching frequency, and the THD

of motor current as function of speed and load are evaluated.

These analytical ﬁndings are compared with simulation results

at every step. The criterion for the selection of optimal hys-

teresis bands depending on the operating point of the motor

is also presented in the same section. The implementation

details of the FPGA platform for the proposed control structure

are presented in Section III. Experimental results are given

in Section IV, which also include detailed comparison with

analytical ﬁndings, followed by conclusions in Section V.

II. A

NA LYT I C A L ANA LY S I S O F DTC

A. Basics of DTC

Henceforth, wherever DTC i s mentioned, it is referred to the

original conventional hysteresis type [1]. The common realiza-

tion of ac motor controls is on a digital signal processor (DSP).

Such a realization incorporates computational delay and, hence,

a dead time in the control loop, which is typically in the range

of 25–100 μs. With such a realization, the DTC performance

cannot be accurately predicted. To have an accurate analysis,

it is necessary to assume continuous-time realization or very

small sampling time, which can be approximated to continuous.

The block diagram representation of the DTC is shown in

Fig. 1. For the analysis, the intention was to use a high-

speed and dynamic motor; hence, commercially available new-

age concentrated winding servo PMSM with surface-mounted

magnets is chosen (for motor details, see the Appendix).

The idea of torque control in the DTC is to control the angle

between the stator- and rotor-ﬂux vectors, which is known as

the torque angle δ

. The position of the stator-ﬂux vector in the

hexagon (as marked in Fig. 2) needs to be determined in order to

control the torque angle. With this information, to increase the

torque, the ﬂux vector is accelerated from the present position

in the direction of the rotation with the help of appropriate

active voltage vectors. For example, in sector 1, the voltage

vectors v

and v

are used (see Fig. 2); v

increases both

the ﬂux magnitude and the torque, whereas v

increases the

torque but reduces the ﬂux magnitude. Similarly, for sector-2

vectors (v

), sectors 3 (v

),4(v

),5(v

), and 6

) are used. The torque produced increases with the sine

of the angle between the s tator- and rotor-ﬂux vectors. At lower

speeds, the stator-ﬂux vector can be moved away from the rotor

ﬂux very quickly, which implies faster torque increase. This

behavior slows down as the speed increases because the rotor-

ﬂux vector is following up with higher speed.

The torque produced in a PMSM is the result of the inter-

action between the rotor ﬂux, i.e., the permanent ﬂux of the

magnets, and the stator current. The stator-ﬂux linkage consists

of rotor-ﬂux linkage and the part contributed by the stator cur-

rent via the armature inductance. Therefore, unlike the case of

induction machines (with ﬁeld oriented control (FOC)), in the

PMSM, the ﬂux-magnitude reference is a function of the torque

reference, depicted in Fig. 1. To keep the switching frequency

low, active vectors are used to increase the torque, whereas

for reducing the torque, the zero-voltage vector is applied in

case of positive speed. In case of negative speed, the strategy is

opposite. The angle and the magnitude of the ﬂux assumed to

be unchanged during the application of zero-voltage vector be-

cause of the negligible resistive drop. Hence the ﬂux-controller

output is expected to remain unchanged during this period.

From the basic understanding of hysteresis controllers, it is

evident that the switching signals will not periodically change

like in case of PWM controls. Hence, one can deﬁne switching

frequency as the number of pulses (two switch changeovers in

opposite directions count as one pulse) within a time interval.

The time interval should be long enough for better averaging.

The following notations are used for the different frequencies

of the control:

frequency of ﬂux-controller output;

frequency of torque-controller output;

. switching frequency of the inverter (the number of

switch changes of S

or S

, respectively).

The switching frequency of the inverter can be approximated

to the torque- and ﬂux-controller output frequencies as

≈

+ F

(1)

because the switching commands are distributed among the

three phases. From (1), it is evident that F

can be controlled

by controlling F

or F

, or both. Hence it is essential to have

a theoretical analysis on how these individual frequencies vary

with the operating point of the motor.

剩余10页未读，继续阅读

评论收藏

内容反馈

sofiakai

2014-10-15

不错的分享，外面有点难找

ZuoTaiDao

粉丝: 0
资源: 1

直接转矩控制外文资料

直接转矩控制

矿井提升机双馈电动机的直接转矩控制

论文外文资料

单片机软起动控制器的设计附外文翻译.doc

永磁同步电动机外文翻译范文.doc

感应电机控制

PMSM直接转矩控制

直接转矩控制讲座

直接转矩控制_直接转矩控制_

异步电动机直接转矩控制

单片机软起动控制器的设计（附外文翻译）.doc

风力发电机外文文献翻译.docx

步进电机控制器种类用途

机械毕业设计——纯电动汽车电控调速系统设计.zip

SRM的直接转矩控制

异步电机直接转矩控制

直接转矩控制仿真

DTC_直接转矩控制_

直接转矩控制_直接转矩_永磁同步电机_直接转矩控制_

串口助手工具合集.zip

OLED显示温度和时间-STM32F103C8T6（完整程序工程+原理图+相关资料）.zip

最新资源