
Introduction:
The aim of the ECG simulator is to produce the typical ECG waveforms of different
leads and as many arrhythmias as possible. My ECG simulator is a matlab based
simulator and is able to produce normal lead II ECG waveform.
The use of a simulator has many advantages in the simulation of ECG waveforms.
First one is saving of time and another one is removing the difficulties of taking real
ECG signals with invasive and noninvasive methods. The ECG simulator enables us
to analyze and study normal and abnormal ECG waveforms without actually using
the ECG machine. One can simulate any given ECG waveform using the ECG
simulator.
Significant features of ECG waveform:
A typical scalar electrocardiographic lead is shown in Fig. 1, where the significant
features of the waveform are the P, Q, R, S, and T waves, the duration of each wave,
and certain time intervals such as the P-R, S-T, and Q-T intervals.
fig 1.Typical ECG signal

Main features of this simulator:
• Any value of heart beat can be set
• Any value of intervals between the peaks (ex-PR interval) can be set
• Any value of amplitude can be set for each of the peaks
• Fibrillation can be simulated
• Noise due to the electrodes can be simulated
• Heart pulse of the particular ECG wave form can be represented in a separate
graph
Principle:
Fourier series
Any periodic functions which satisfy dirichlet’s condition can be expressed as a
series of scaled magnitudes of sin and cos terms of frequencies which occur as a
multiple of fundamental frequency.
∞ ∞
f (x) = (a /2) + Σ a
o n
cos (nπx / l) + Σ b
n
sin (nπx / l),
n=1 n=1
a = (1/ l ) ∫ f (x) dx , T = 2l --Æ (1)
o
T
a = (1/ l ) ∫ f (x) cos (nπx / l) dx , n = 1,2,3…. --Æ (2)
n
T
b = (1/ l ) ∫ f (x) sin (nπx / l) dx , n = 1,2,3…. --Æ (3)
n
T
ECG signal is periodic with fundamental frequency determined by the heart beat. It
also satisfies the dirichlet’s conditions:
• Single valued and finite in the given interval
• Absolutely integrable
• Finite number of maxima and minima between finite intervals
• It has finite number of discontinuities
Hence fourier series can be used for representing ECG signal.
Calculations:
If we observe figure1, we may notice that a single period of a ECG signal is a
mixture of triangular and sinusoidal wave forms. Each significant feature of ECG
signal can be represented by shifted and scaled versions one of these waveforms as
shown below.
• QRS, Q and S portions of ECG signal can be represented by triangular
waveforms
• P, T and U portions can be represented by triangular waveforms
Once we generate each of these portions, they can be added finally to get the ECG
signal.
Lets take QRS waveform as the centre one and all shiftings takes place with respect
to this part of the signal.
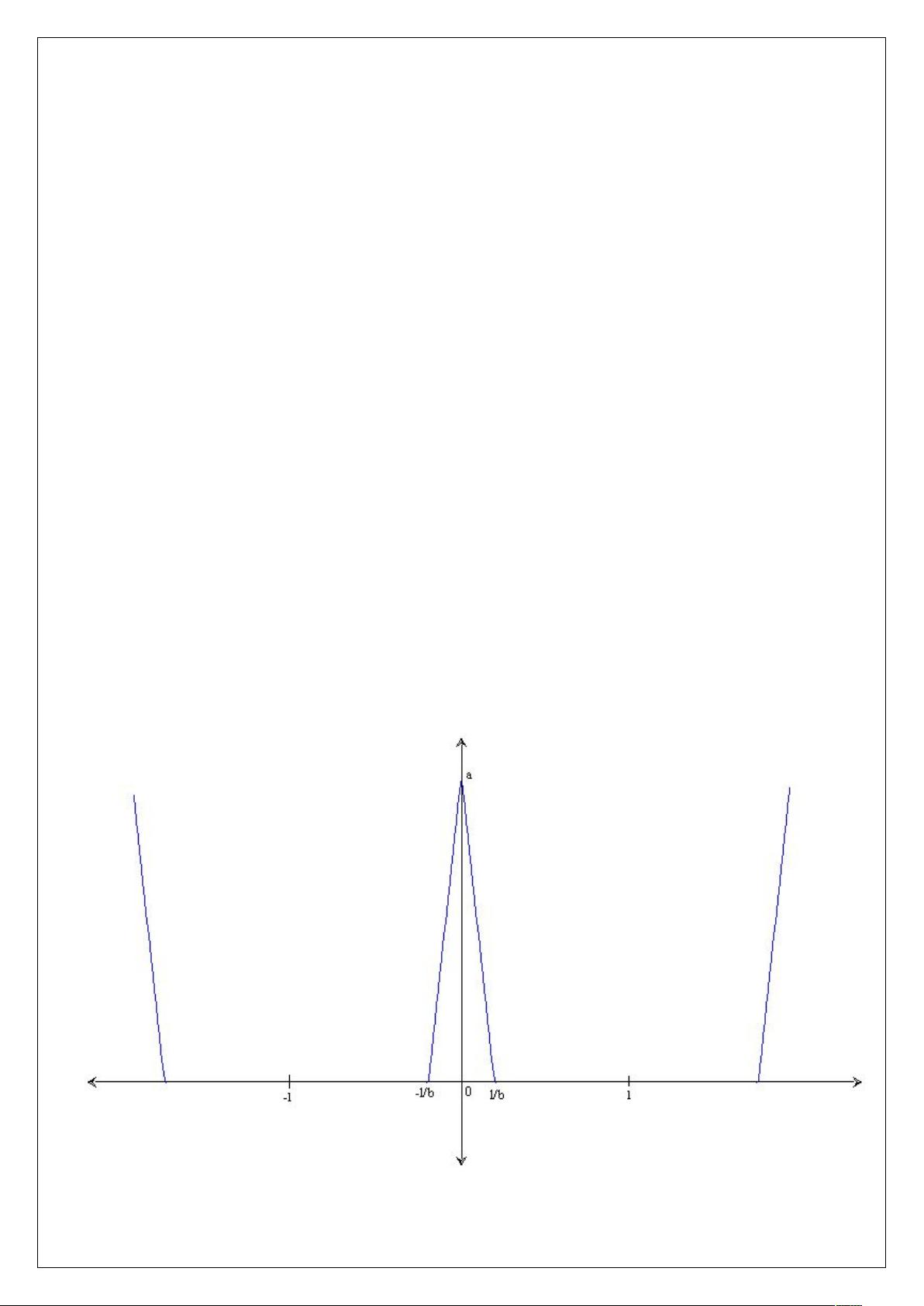
How do we generate periodic QRS portion of ECG signal
Fig 2. generating QRS waveform




















- 1
- 2
- 3
前往页