在土木工程设计和绘图中,掌握二维图形的绘制与三维空间概念的理解是一项基础而关键的工作,这是由《画法几何及土木工程制图》这一课程来实现的。画法几何作为工程制图的理论基础,其核心在于直线的投影及其相关概念。直线的投影不仅是学习画法几何的起点,也是深入理解工程图纸绘制方法的关键。
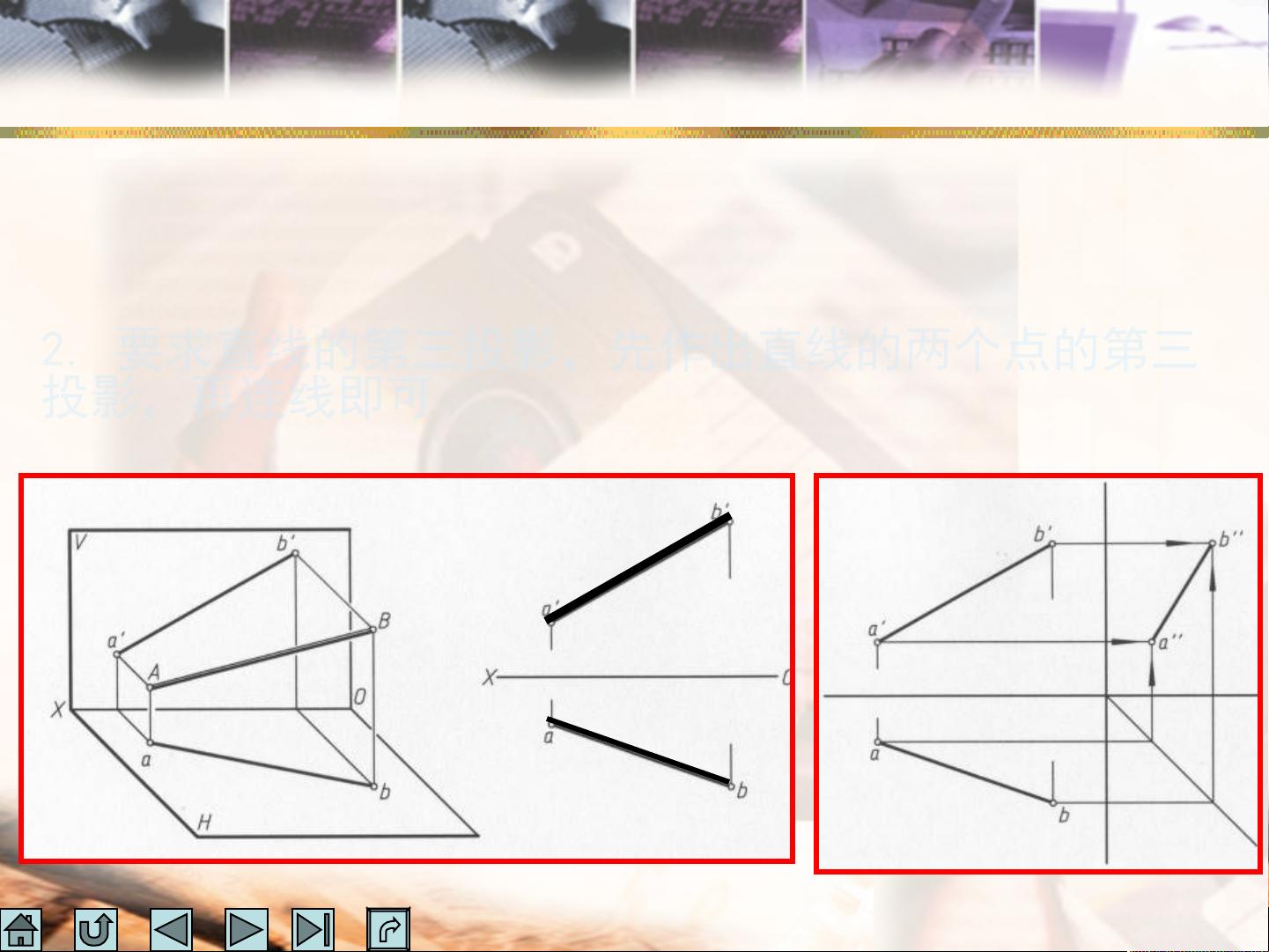
直线的投影基于画法几何中一个重要的原理:任何一条直线都可以看作是无数个点的集合。因此,当我们谈论直线的投影时,实际上是讨论这些点在不同投影面上的投影所形成的图形。在实际操作中,如果需要绘制一条直线的投影,只需要知道其上两个点的投影位置,连接这两个点的投影即可得到整条直线的投影。
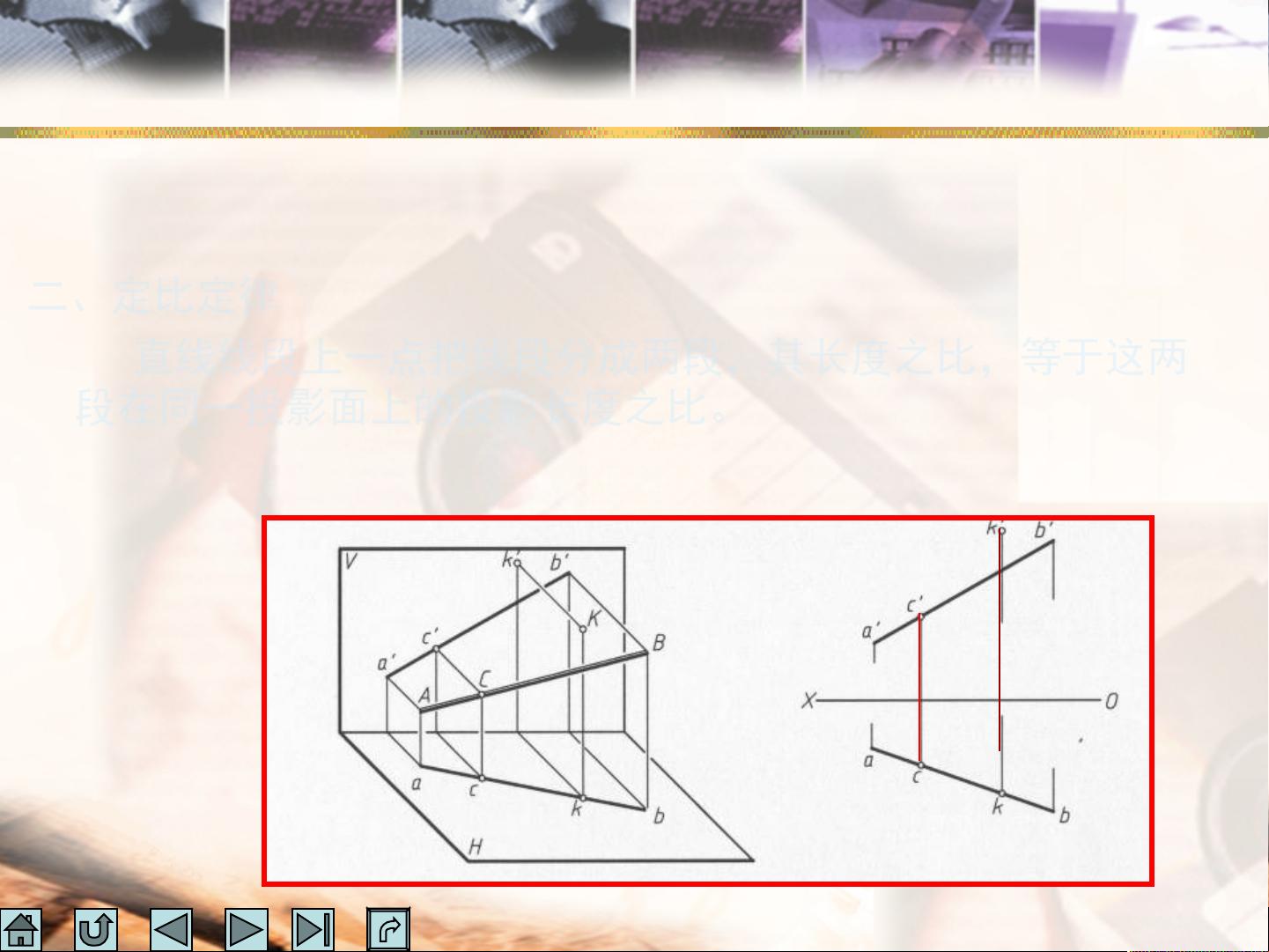
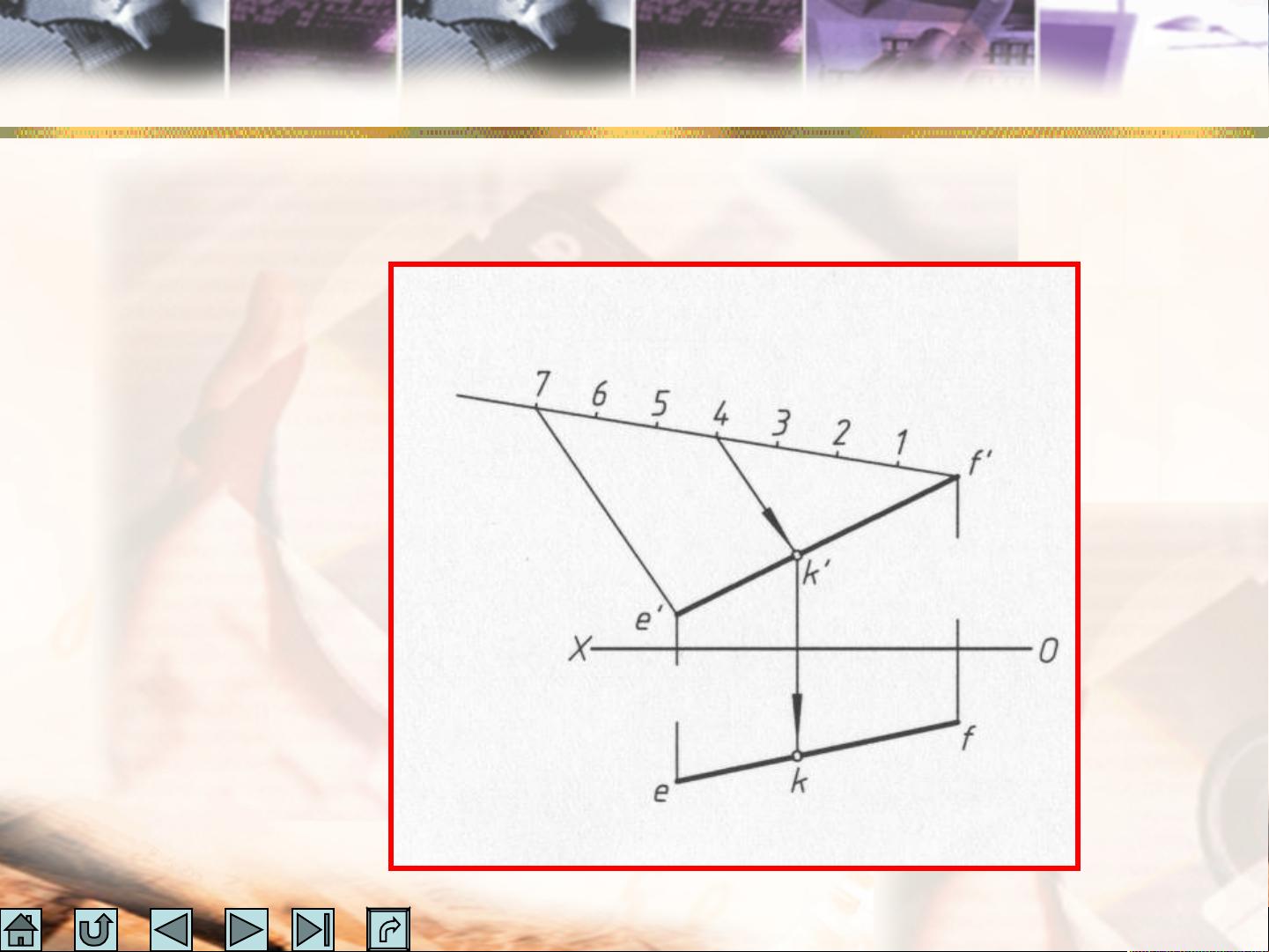
在此基础上,我们要特别关注迹点的概念。迹点是指直线与投影面交点的位置,根据直线与投影面的相对位置关系,迹点可细分为水平迹点、正面迹点和侧面迹点。迹点之所以重要,是因为它们在相应的投影面上的投影是迹点本身,而在其他投影面上则会表现为直线投影与投影轴的交点。了解迹点的这些特性,有助于我们在复杂的工程图纸中快速而准确地定位直线元素。
此外,直线的倾角和实长是分析直线在不同投影面中表现的两个重要参数。倾角是指直线与投影面之间的夹角,实长则是直线在空间中的实际长度。要解决倾角和实长的问题,常用的工具是直角三角形法,通过这种作图方法,可以在已知一个投影和倾角的情况下,求出直线的其他投影和实长。
在工程图中,直线可以有不同的位置关系,包括投影面平行线、投影面垂直线以及处于一般位置的直线。每种位置关系的直线在投影时都有其特定的属性。例如,投影面垂直线在相应的投影面上积聚为一点,而其他两个投影则与投影轴垂直,且能直接反映线段的实际长度。而投影面平行线在某个特定的投影面上表现为平行线,在其他两个投影面上则表现为直线段。这些不同的投影特性让我们能够在二维图纸上准确表达三维空间中的直线关系。
《画法几何及土木工程制图》课程所教授的这些基础理论和规则,是土木工程师在进行结构设计、绘制施工图和解决工程问题时所不可或缺的。掌握画法几何的知识能使得工程师在表达和沟通设计理念时更加准确,确保设计意图得到完整而精确的实施。画法几何的知识能够帮助工程师在图纸上更加清晰地表达复杂的几何关系,为建筑施工提供详实的依据。
在土木工程实践中,绘图技术是沟通工程师与建筑者之间的桥梁。良好的绘图技能可以减少误解和错误,提高工程效率,降低施工成本。因此,无论是对于工程教育还是实际工程应用,深入学习《画法几何及土木工程制图》都是提升工程师专业能力的重要途径。通过系统学习直线投影、三维空间的分析以及图纸表达等画法几何的基本原理,工程师能够更好地把握工程设计的全局,从而在土木工程领域做出更科学、更有效的贡献。