
概念、性质、定理、公式必须清楚,解法必须熟练,计算必须准确
:全体 维实向量构成的集合 叫做 维向量空间.
1

√ 关于 :
①称为 的标准基, 中的自然基,单位坐标向量 ;
② 线性无关;
③ ;
④ ;
⑤任意一个 维向量都可以用 线性表示.
行列式的定义
√ 行列式的计算:
①行列式按行(列)展开定理:行列式等于它的任一行(列)的各元素与其对应的代数余子式的乘积之和.
2

推论:行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零.
②若 都是方阵(不必同阶),则 (拉普拉斯展开式)
③上三角、下三角、主对角行列式等于主对角线上元素的乘积.
④关于副对角线: (即:所有取自不同行不同列的 个元素的乘积的代数和)
⑤范德蒙德行列式:
矩阵的定义 由 个数排成的 行 列的表 称为 矩阵.记作: 或
3
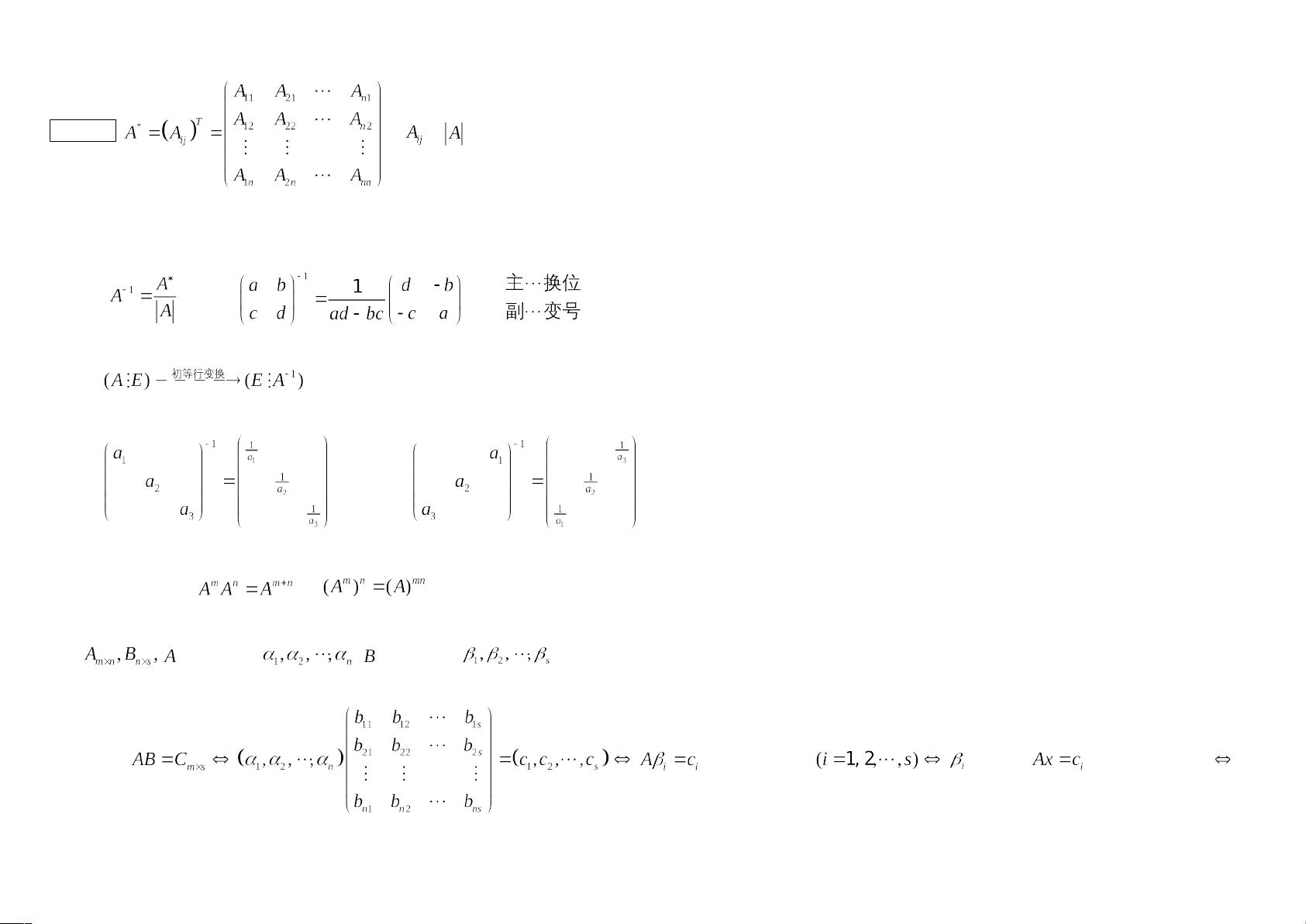
伴随矩阵 , 为 中各个元素的代数余子式.
√ 逆矩阵的求法:
① :
②
③
√ 方阵的幂的性质:
√ 设 的列向量为 , 的列向量为 ,
则 , 为 的 解
4

可由 线性表示.即: 的列向量能由 的列向量线性表示, 为系数矩阵.
同理: 的行向量能由 的行向量线性表示, 为系数矩阵.
即:
√ 用对角矩阵 乘一个矩阵,相当于用 的对角线上的各元素依次乘此矩阵的向量;
用对角矩阵 乘一个矩阵,相当于用 的对角线上的各元素依次乘此矩阵的向量.
√ 两个同阶对角矩阵相乘只用把对角线上的对应元素相乘.
√ 分块矩阵的转置矩阵:
分块矩阵的逆矩阵:
分块对角阵相乘: ,
5















