FastandRobustMulti-FrameSuper-Resolution_multiframe资源-CSDN文库

需积分: 10 45 浏览量 2014-02-28 09:51:54 上传评论收藏 5.07MB PDF 举报

This paper propose an alternate approach using L1 norm minimization and robust regularization based on a bilateral prior to deal with different data and noise models. 本文的主题是多帧超分辨率重构技术的研究，重点关注的是如何从一系列低分辨率的图像中重建出一个或一组高分辨率的图像。文章提出了一种新的方法，通过L1范数最小化和基于双边先验的鲁棒正则化来处理不同数据和噪声模型的问题。该方法具有计算成本低，能够抵御运动和模糊估计中的误差，并能够生成边缘锐利的图像。在详细讨论之前，我们先来解释几个关键词汇： 1. 超分辨率重构（Super-Resolution Reconstruction）：这一术语指的是利用一系列低分辨率图像通过某些计算方法得到一个或多个高分辨率图像的过程。 2. L1范数最小化（L1 Norm Minimization）：在数学中，L1范数通常是指向量元素绝对值之和。在图像处理中，通过最小化L1范数，可以找到一个最接近原始图像的估计。 3. 鲁棒性（Robustness）：指的是算法或模型对于输入数据的微小变化、噪声或其他不确定因素的不敏感性，即鲁棒性好的模型能较好地保持性能。 4. 双边滤波（Bilateral Filter）：一种图像滤波算法，它在进行滤波时考虑了像素间的空间距离和像素值的相似度，因此可以在保持边缘信息的同时平滑图像。 5. 正则化（Regularization）：在数学和计算机科学中，正则化是一种改进算法性能的手段，通过加入额外的规则或约束来避免模型过于复杂（过拟合）。现在，我们来具体分析文章中提到的知识点：文章开篇提到了超分辨率技术在过去二十年中发展迅速，提出了多种方法。这些方法通常对所假设的数据和噪声模型非常敏感，这限制了它们的实用性。作者提出了一种新的方法，这种方法使用双边先验的鲁棒正则化，能够有效处理不同的数据和噪声模型。文章中提到的双边滤波是一种非线性的滤波技术，与传统的线性滤波方法不同，双边滤波能够同时考虑空间上的邻近性和像素值的相似性。在超分辨率重建中，使用双边滤波可以有效减少图像噪声同时保持图像边缘清晰。在引入所提方法之前，文章先介绍了成像设备在理论和实践上都存在一定的分辨率限制。成像过程可以看作是连续强度分布的动态场景，因为相对运动，场景会在相机镜头前变形。图像会因为大气湍流和相机镜头的点扩散函数而变得模糊。然后，图像会在CCD上被离散化，最终得到数字化的噪声帧。作者使用了一种前向模型来表示这一过程。在提出新的方法后，作者强调了此方法的计算成本低廉，对于运动估计和模糊估计中的误差具有鲁棒性，并且能够产生具有锐利边缘的图像。文章最后通过仿真结果验证了所提方法的有效性，并与其他超分辨率方法相比显示出了优越性。所提到的索引项包含双向滤波、去模糊、增强、图像恢复、多帧、正则化、鲁棒估计和全变分（TV）等。这表明文章的技术涉及到了图像处理的多个方面，并结合了多帧处理技术、鲁棒性以及图像增强等方法。整体而言，这篇文章对超分辨率图像重建技术领域提供了重要的理论和实际贡献，特别是通过提出一种新的基于双边滤波的鲁棒正则化方法，大大提高了超分辨率重建的质量和鲁棒性，具有很好的应用前景。

资源推荐

资源详情

资源评论

IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 13, NO. 10, OCTOBER 2004 1327

Fast and Robust Multiframe Super Resolution

Sina Farsiu, M. Dirk Robinson, Student Member, IEEE, Michael Elad, and Peyman Milanfar, Senior Member, IEEE

Abstract—Super-resolution reconstruction produces one or a set

of high-resolution images from a set of low-resolution images. In

the last two decades, a variety of super-resolution methods have

been proposed. These methods are usually very sensitive to their

assumed model of data and noise, which limits their utility. This

paper reviews some of these methods and addresses their short-

comings. We propose an alternate approach using

norm min-

imization and robust regularization based on a bilateral prior to

deal with different data and noise models. This computationally in-

expensive method is robust to errors in motion and blur estimation

and results in images with sharp edges. Simulation results conﬁrm

the effectiveness of our method and demonstrate its superiority to

other super-resolution methods.

Index Terms—Bilateral ﬁlter, deblurring, enhancement, image

restoration, multiframe, regularization, robust estimation, super

resolution, total variation (TV).

I. INTRODUCTION

HEORETICAL and practical limitations usually constrain

the achievable resolution of any imaging device. A dy-

namic scene with continuous intensity distribution

seen to be warped at the camera lens because of the relative mo-

tion between the scene and camera. The images are blurred both

by atmospheric turbulence and camera lens by continuous point

spread functions

and . Then, they will

be discretized at the CCD resulting in a digitized noisy frame

. We represent this forward model by the following:

(1)

in which

is the two-dimensional convolution operator, is

the warping operator,

is the discretizing operator, is

the system noise, and

is the resulting discrete noisy and

blurred image. Fig. 1 illustrates this equation.

Super resolution is the process of combining a sequence of

low-resolution (LR) noisy blurred images to produce a higher

resolution image or sequence. The multiframe super-resolution

Manuscript received July 21, 2003; revised January 13, 2004. This work

was supported in part by the National Science Foundation under Grant

CCR-9984246, in part by the U.S. Air Force under Grant F49620–03-1-0387,

and in part by the National Science Foundation Science and Technology Center

for Adaptive Optics, managed by the University of California, Santa Cruz,

under Cooperative Agreement AST-9876783. The associate editor coordinating

the review of this manuscript and approving it for publication was Prof. Robert

D. Nowak.

S. Farsiu, M. D. Robinson, and P. Milanfar are with the Electrical Engi-

neering Department, University of California, Santa Cruz, CA 95064 USA

(e-mail: farsiu@ee.ucsc.edu; dirkr@ee.ucsc.edu; milanfar@ee.ucsc.edu).

M. Elad is with the Computer Science Department, The Technion–Israel In-

stitute of Technology, Haifa, Israel (e-mail: elad@cs.technion.ac.il).

Digital Object Identiﬁer 10.1109/TIP.2004.834669

Fig. 1. Block diagram representation of (1), where

(

x; y

)

is the continuous

intensity distribution of the scene,

[

m; n

]

is the additive noise, and

[

m; n

]

is the resulting discrete low-quality image.

problem was ﬁrst addressed in [1], where they proposed a fre-

quency domain approach, extended by others, such as [2]. Al-

though the frequency domain methods are intuitively simple and

computationally cheap, they are extremely sensitive to model er-

rors [3], limiting their use. Also, by deﬁnition, only pure trans-

lational motion can be treated with such tools and even small

1328 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 13, NO. 10, OCTOBER 2004

deviations from translational motion signiﬁcantly degrade per-

formance.

Another popular class of methods solves the problem of reso-

lution enhancement in the spatial domain. Non-iterative spatial

domain data fusion approaches were proposed in [4]–[6]. The

iterative back-projection method was developed in papers such

as [7] and [8]. In [9], the authors suggested a method based on

the multichannel sampling theorem. In [10], a hybrid method,

combining the simplicity of ML with proper prior information

was suggested.

The spatial domain methods discussed so far are generally

computationally expensive. The authors in [11] introduced a

block circulant preconditioner for solving the Tikhonov regular-

ized super-resolution problem formulated in [10] and addressed

the calculation of regularization factor for the under-determined

case by generalized cross validation in [12]. Later, a very fast

super-resolution algorithm for pure translational motion and

common space invariant blur was developed in [5]. Another

fast spatial domain method was recently suggested in [13],

where LR images are registered with respect to a reference

frame deﬁning a nonuniformly spaced high-resolution (HR)

grid. Then, an interpolation method called Delaunay trian-

gulation is used for creating a noisy and blurred HR image,

which is subsequently deblurred. All of the above methods

assumed the additive Gaussian noise model. Furthermore,

regularization was either not implemented or it was limited to

Tikhonov regularization. Considering outliers, [14] describes a

very successful robust super-resolution method, but lacks the

proper mathematical justiﬁcation ( limitations of this robust

method and its relation to our proposed method are discussed

in Appendix B). Finally, [15] and [16] have considered quan-

tization noise resulting from video compression and proposed

iterative methods to reduce compression noise effects in the

super-resolved outcome.

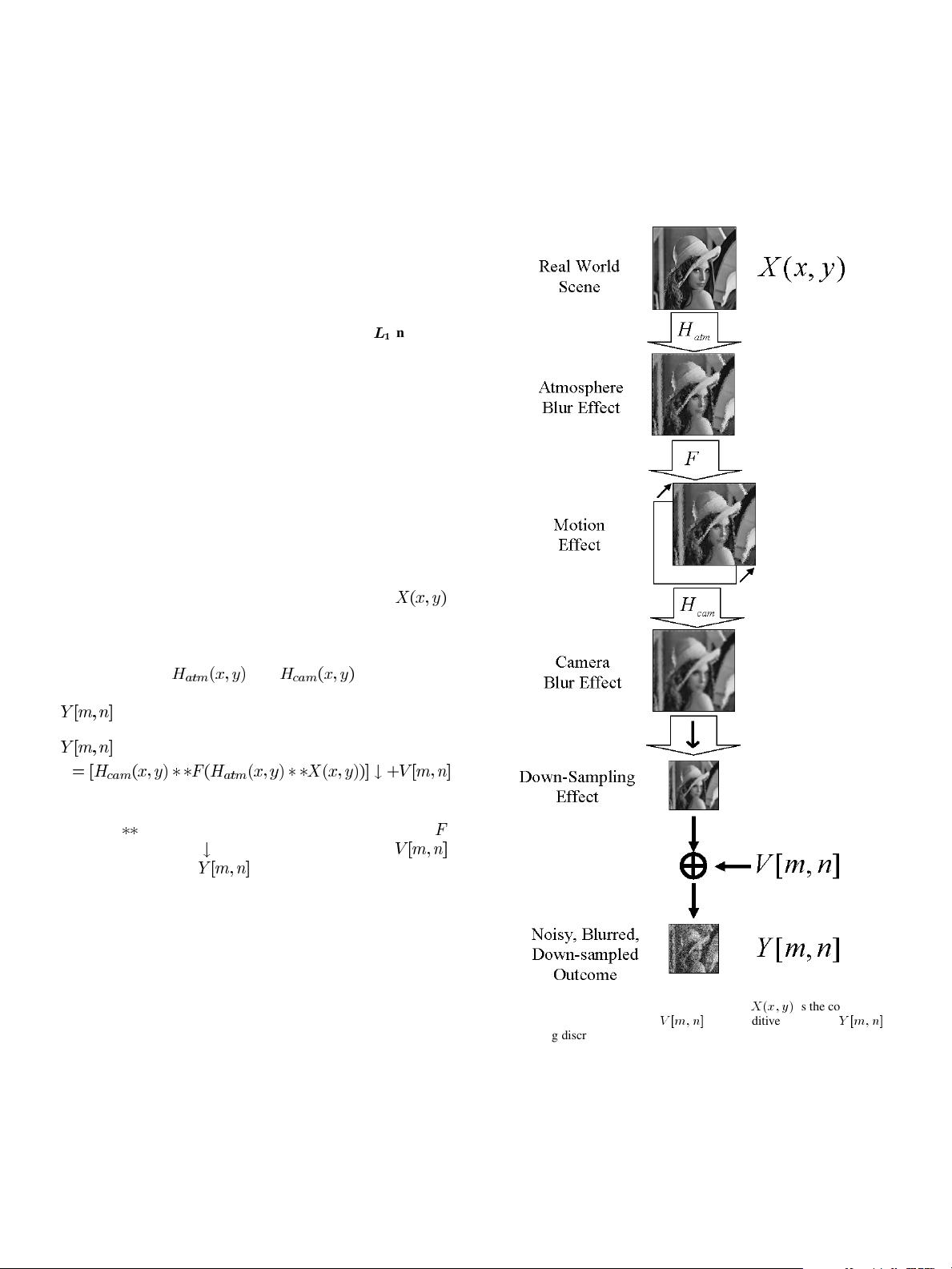
The two most common matrix notations used to formulate the

general super-resolution model of (1) represent the problem in

the pixel domain. The more popular notation used in [5], [11],

and [14] considers only camera lens blur and is deﬁned as

(2)

where the

matrix is the geometric motion

operator between the HR frame

(of size ) and the

th LR frame (of size ) which are rearranged in

lexicographic order and

is the resolution enhancement factor.

The camera’s point spread function (PSF) is modeled by the

blur matrix , and matrix

represents the decimation operator. The vector

is the system noise and is the number of available LR frames.

Considering only atmosphere and motion blur, [13] recently

presented an alternate matrix formulation of (1) as

(3)

In conventional imaging systems (such as video cameras),

camera lens blur has a more important effect than the atmo-

spheric blur (which is very important for astronomical images).

In this paper, we use the model (2). Note that, under some

assumptions which will be discussed in Section II-B, blur and

motion matrices commute and the general matrix super-resolu-

tion formulation from (1) can be rewritten as

(4)

Deﬁning

merges both models into a form

similar to (2).

In this paper, we propose a fast and robust super-resolution al-

gorithm using the

norm, both for the regularization and the

data fusion terms. Whereas the former is responsible for edge

preservation, the latter seeks robustness with respect to motion

error, blur, outliers, and other kinds of errors not explicitly mod-

eled in the fused images. We show that our method’s perfor-

mance is superior to what was proposed earlier in [5], [11], [14],

etc., and has fast convergence. We also mathematically justify a

noniterative data fusion algorithm using a median operation and

explain its superior performance.

This paper is organized as follows. Section II explains the

main concepts of robust super resolution. Section II-B justiﬁes

using the

norm to minimize the data error term; Section II-C

justiﬁes using our proposed regularization term. Section II-D

combines the results of the two previous sections and explains

our method and Section II-E proposes a faster implementation

method. Simulations on both real and synthetic data sequences

are presented in Section III, and Section IV concludes this paper.

II. R

OBUST SUPER

RESOLUTION

A. Robust Estimation

Estimation of an unknown HR image is not exclusively based

on the LR measurements. It is also based on many assumptions

such as noise or motion models. These models are not supposed

to be exactly true, as they are merely mathematically convenient

formulations of some general prior information.

From many available estimators, which estimate a HR image

from a set of noisy LR images, one may choose an estimation

method which promises the optimal estimation of the HR frame,

based on certain assumptions on data and noise models. When

the fundamental assumptions of data and noise models do not

faithfully describe the measured data, the estimator performance

degrades. Furthermore, existence of outliers, which are deﬁned

as data points with different distributional characteristics than

the assumed model, will produce erroneous estimates. A method

which promises optimality for a limited class of data and noise

models may not be the most effective overall approach. Often,

suboptimal estimation methods which are not as sensitive to

modeling and data errors may produce better and more stable

results (robustness).

To study the effect of outliers, the concept of a breakdown

point has been used to measure the robustness of an algorithm.

The breakdown point is the smallest percentage of outlier con-

tamination that may force the value of the estimate outside some

range [17]. For instance, the breakdown point of the simple

mean estimator is zero, meaning that one single outlier is sufﬁ-

cient to move the estimate outside any predicted bound. A robust

estimator, such as the median estimator, may achieve a break-

down equal to 0.5, which is the highest value for breakdown

FARSIU et al.: FAST AND ROBUST MULTIFRAME SUPER RESOLUTION 1329

points. This suggests that median estimation may not be affected

by data sets in which outlier contaminated measurements form

less that 50% of all data points.

A popular family of estimators are the ML-type estimators (M

estimators) [18]. We rewrite the deﬁnition of these estimators

in the super resolution context as the following minimization

problem:

(5)

or by an implicit equation

(6)

where

is measuring the “distance” between the

model and measurements and

. The ML estimate of

for an assumed underlying family of exponential

densities

can be achieved when

To ﬁnd the ML estimate of the HR image, many papers such

as [2], [5], and [11] adopt a data model such as (2) and model

(additive noise) as white Gaussian noise. With this noise

model, least-squares approach will result in the ML estimate

[19]. The least-squares formulation is achieved when

is the

norm of residual

(7)

For the special case of super resolution, based on [5], we will

show in the next section, that least-squares estimation has the

interpretation of being a nonrobust mean estimation. As a result,

least squares-based estimation of a HR image, from a data set

contaminated with non-Gaussian outliers, produces an image

with visually apparent errors.

To appreciate this claim and study the visual effects of dif-

ferent sources of outliers in a video sequence, we set up the

following experiments. In these experiments, four LR images

were used to reconstruct a higher resolution image with two

times more pixels in vertical and horizontal directions [a resolu-

tion enhancement factor of two using the least-squares approach

(7)]. Fig. 2(a) shows the original HR image and Fig. 2(b) shows

one of these LR images which has been acquired by shifting

Fig. 2(a) in vertical and horizontal directions and subsampling

it by factor of two (pixel replication is used to match its size with

other pictures).

In the ﬁrst experiment one of the four LR images contained

afﬁne motion with respect to the other LR images. If the model

assumes translational motion, this results in a very common

source of error when super resolution is applied to real data se-

quences, as the respective motion of camera and the scene are

seldom pure translational. Fig. 2(c) shows this outlier image.

Fig. 2(d) shows the effect of this error in the motion model

(shadows around Lena’s hat) when the non robust least-squares

approach [5] is used for reconstruction.

To study the effect of non-Gaussian noise models, in the

second experiment all four LR images were contaminated with

salt and pepper noise. Fig. 2(e) shows one of these LR images

and Fig. 2(f) is the outcome of the least-squares approach for

reconstruction.

As the outlier effects are visible in the output results of least-

squares-based super-resolution methods, it seems essential to

ﬁnd an alternative estimator. This new estimator should have

the essential properties of robustness to outliers and fast imple-

mentation.

B. Robust Data Fusion

In Section II-A, we discussed the shortcomings of least

squares-based HR image reconstruction. In this subsection,

we study the family of

, norm estimators. We

choose the most robust estimator of this family and show how

implementation of this estimator requires minimum memory

usage and is very fast.

The following expression formulates the

minimization

criterion:

(8)

Note that if

, then (8) will be equal to (7).

Considering translational motion and with reasonable as-

sumptions such as common space-invariant PSF, and similar

decimation factor for all LR frames (i.e.,

and

which is true when all images are acquired with a

unique camera), we calculate the gradient of the

cost. We

will show that

norm minimization is equivalent to pixelwise

weighted averaging of the registered frames. We calculate these

weights for the special case of

norm minimization and show

that

norm converges to median estimation which has the

highest breakpoint value.

Since

and are block circulant matrices, they commute

(

and ). Therefore, (8) may be

rewritten as

(9)

We deﬁne

. So, is the blurred version of the ideal

HR image

. Thus, we break our minimization problem in two

separate steps:

1) ﬁnding a blurred HR image from the LR measurements

(we call this result

);

2) estimating the deblurred image

from .

Note that anything in the null space of

will not converge by

the proposed scheme. However, if we choose an initialization

that has no gradient energy in the null space, this will not pose

a problem (see [5] for more details). As it turns out, the null

space of

corresponds to very high frequencies, which are not

part of our desired solution. Note that addition of an appropriate

regularization term (Section II-C) will result in a well-posed

problem with an empty null space. To ﬁnd

, we substitute

with

(10)

剩余17页未读，继续阅读

评论收藏

内容反馈

zhaoxunjie

粉丝: 0
资源: 9

Fast and Robust Multi-Frame Super-Resolution

最新资源

Fast and Robust Multi-Frame Super-Resolution

三次样条插值代码matlab-MultiFrameSuperResolution:基于Matlab的多帧超分辨率工具

Multi-Frame Video Super-Resolution Using Convolutional Neural Networks

Fast-a-Robust-Super-Resolution(BTV).zip_BTV_TV super resolution

Single Image Super Resolution Based on Multi-scale Self-Similarity Structure in The CS Frame

论文1_Fast Direct Super-Resolution by Simple Functions ICCV 20131

Registration-Reliability Based Strategy to EnhanceMulti-Frame Super-Resolution Algorithms

Bidirectional Recurrent Convolutional Networks for Multi-Frame Super-Resolution

讲稿_Robust Multi-Modality Multi-Object Tracking.docx

演示-Robust Multi-Modality Multi-Object Tracking.pptx

Robust Multi-Exposure Image Fusion: A Structural Patch Decomposition Approach

robust multi-period portfolio selection .pdf

A Practical and Robust Bump-mapping Technique for Today's GPUs

2018(FRVSR)Frame Recurrent Video Super Resolution.pdf

A Fast Image Super-Resolution Algorithm Using an Adaptive Wiener Filter.pdf

Robust Multi-Resolution Pedestrian Detection in Traffic Scences

论文研究-Fast Video Stream Super Resolution Reconstruction based on CUDA.pdf

FREE A Fast and Robust End-to-End Video Text Spotter个人论文解读

FRSR_Fast and robust multiframe super resolution 多帧超分辨率重建_退化图像获得

Simple, Accurate, and Robust Projector-Camera Calibration.pdf

A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms

Complete and robust no-fit polygon generation for the irregular stock cutting problem

Discriminatively Trained Particle Filters for Complex Multi-Object Tracking

Hybrid-MVS Robust Multi-View Reconstruction With Hybrid.pdf

几篇CVPR关于multi-task的整理

5-Robust multi-period portfolio model based on prospect theory.pdf

Robust Real-time Object Detection 论文 整理ppt 及一篇相关中文论文

Robust Optimization-Directed Design

最新资源

Robust Real-time Object Detection 论文整理ppt 及一篇相关中文论文