
安徽建筑工业学院
课 程 设 计 报 告
课程名称: 数值分析
题 目: 用三次样条插值设计中英文签名
院 系: 数理系
专 业: 信息与计算科学
班 级: 07
信息 2 班
学 号: 07207010223
姓 名: 赵双祥
时 间: 2010-01- 03 — 2010-01- 11
目 录

数值分析课程设计报告——中英文设计签名
一、 理论分析 2
1.1 问题分析..........................................................................................................................................2
1.2 理论依据..........................................................................................................................................2
1.3 求解对策..........................................................................................................................................3
二、 算法设计(推导、求解) 4
2.1 三次样条插值函数的定义.............................................................................................................4
2.2 三次样条插值算法推导、求解......................................................................................................4
三、 程序设计(分析、程序框图)9
3.1 GINPUT()程序分析...........................................................................................................................9
3.2 三次样条插值程序分析.................................................................................................................9
3.3 图像(签名)输出程序分析........................................................................................................11
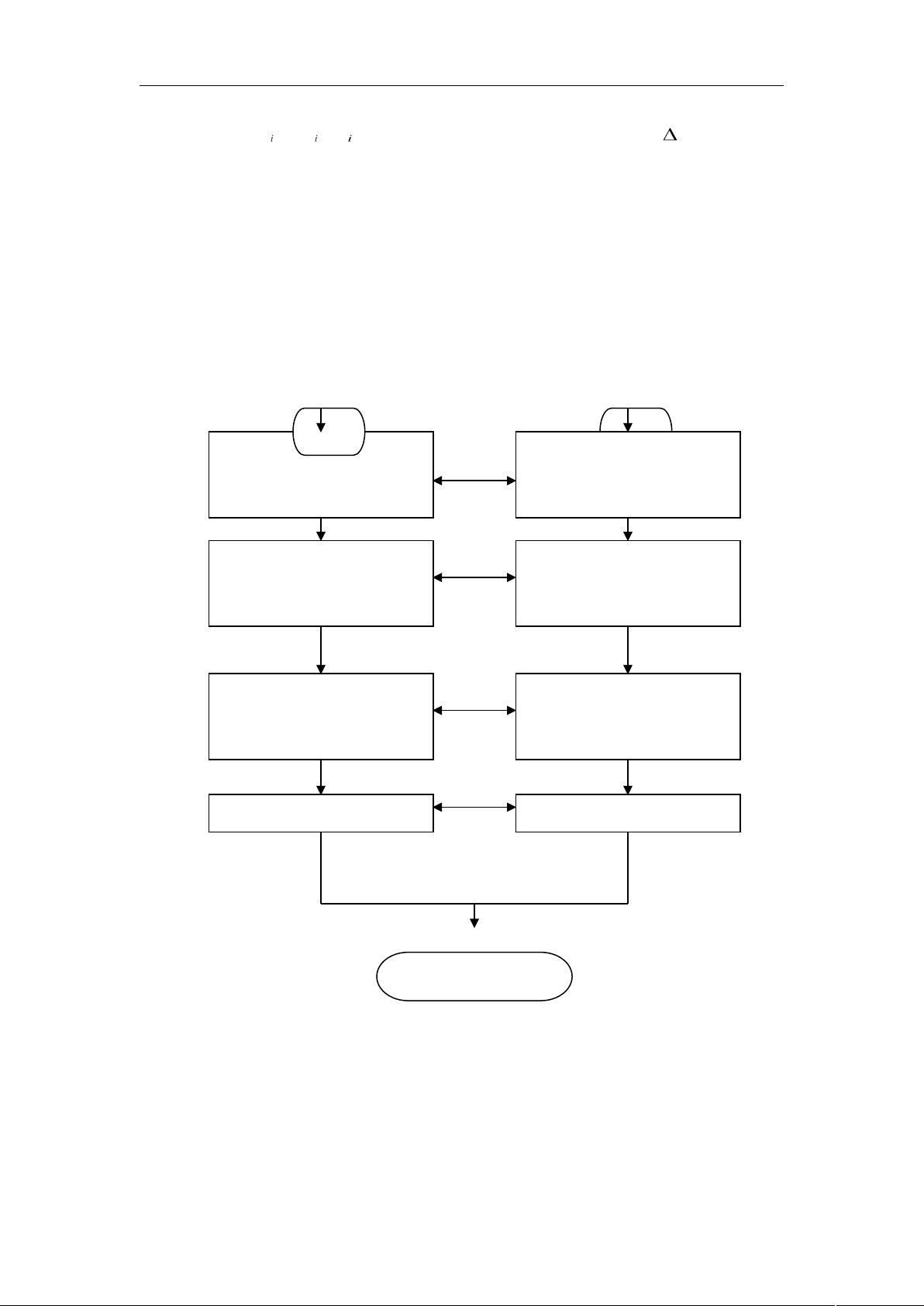
3.4 程序框图........................................................................................................................................11
四、 签名验证(应用实例) 12
4.1 程序清单.......................................................................................................................................12
4.2 图形演示.......................................................................................................................................12
4.3 计算结果输出...............................................................................................................................15
五、 效果分析 17
5.1 效果对比........................................................................................................................................19
5.2 结果解释........................................................................................................................................20
六、 附录 21
6.1 第一种方法程序............................................................................................................................21
6.2 第二种方法程序............................................................................................................................22
1

数值分析课程设计报告——中英文设计签名
一、 理论分析
1.1 问题分析
1.1.1 问题描述
(1)设计自己的英文签名,给出一组数据点,用三次样条曲线画出所设计的英文签
名的字体。
(2)设计你的草体汉字签名,给出一组数据点,分别用三次样条曲线画出所设计的中文
签字的字体.
(3)如果设计出的三次样条不满意,怎么改进算法?
1.1.2 分析思想
要设计出英(中)文签名,首先、要获得与自己英(中)文签名相似的一组数据点 ,
最好这组数据点的获取可因名字的改变而改变且简单易行,以适应不同的签名;其次 、
要选用合适的算法,才能设计出较美观的签名,问题要求用三次样条插值做,若效果
不满意,改进时可选择其他算法;最后、选择合适数学工具和备用改进算法,合适的
数学工具能大大简化我们的工作量,获得满意结果。备用的改进算法的提出可以引导
我们在下面的课程设计中注意基本算法的不足,多思考,勤探究。
1.2 理论依据
1.2.1 交互式界面
交互式界面即窗口、光标、按键、菜单、文字说明等对象(Objects)构成的一个
用户界面。用户通过一定的方法(如鼠标或键盘)选择、激活这些图形对象,使计
算机产生某种动作或变化,比如实现获取数据、计算、绘图等。要使数据点可因名
字的改变而改变且简单易行,以适应不同的签名,可采用交互式界面进行操作。如
我们可以用鼠标点击获取名字大致的数据点,显然,不同名字可以实现能得到不同
数据点。在 MATLAB 中,可以用 ginput()函数轻松实现这一功能。
1.2.2 三次样条插值算法
在区间[a,b]上给定有 n+1 个节点的分割 :a=x <x <…<x ]=b。若在
[a,b]上定义的函数 s(x)满足:
(1)在子区间[x ,x ]上 s(x)是最高为三次的多项式,i=0,1,… n-1;
(2)在[a,b]上 s(x)是二阶连续可微函数,即 s(x) C [a.b]。则称 s(x)为
[a,b]上关于分割 的三次样条函数。S(x)对应的曲线称为三次样条曲线。若
s(x)还满足
2
数值分析课程设计报告——中英文设计签名
(3)S(x )=y =f ,i=0,1,…,n 则称 s(x)为[a,b]上关于分割 的三次样条插
值函数,f(x)称为被插函数。
三次样条插值函数对应的曲线称为三次样条插值曲线。
我们知道分段低次插值的优点是具有收敛性与稳定性,缺点是光滑性较差,不能
满足实际需要.例如高速飞机的机翼形线、船体放样形值线、精密机械加工等都要
求有二阶光滑度,即二阶导数连续,通常三次样条(Spline)函数即可满足要求。所
以对于签名,三次样条插值算法完全能够在给定的一组数据点下实现签名效果。
1.3 求解对策
3
获得与签名相似的一组数据
点,最好可因名字的改变而
改变
问题 对策
采用交互式界面进行操作,
用鼠标点击获取名字大致的
数据点
选用合适的算法
三次样条插值算法:可产生
二阶光滑度,即二阶导数连
续签名图样
选用改进算法 双三次插值算法
选用合适的数学工具
MATLAB7.0
实 现英 (中 ) 文签
名

数值分析课程设计报告——中英文设计签名
二、 算法设计(推导、求解)
2.1 三次样条插值函数的定义
样条(Spline)是绘图员用来描绘光滑曲线的均匀有弹性的细长木条(或有机玻
璃条)。
用压铁将木条加以固定使它通过各型值点,最后沿着这根木条画出光滑曲线,作用
与曲线板和云形规相似。我们称这条光滑的曲线为样条曲线,样条曲线对应的函数称
为样条函数。它是连续的光滑的,具有连续变化的曲率,实际上就是一条三次样条曲
线。
定义:在区间[a,b]上给定有 n+1 个节点的分割 :a=x <x <…<x ]=b。
若在[a,b]上定义的函数 s(x)满足:
(1)在子区间[x ,x ]上 s(x)是最高为三次的多项式,i=0,1,… n-1;
(2)在[a,b]上 s(x)是二阶连续可微函数,即 s(x) C [a.b]。则称 s(x)为[a,b]上
关于分割 的三次样条函数。S(x)对应的曲线称为三次样条曲线。若 s(x)还
满足
(3)S(x )=y =f ,i=0,1,…,n 则称 s(x)为[a,b]上关于分割 的三次样条插值函
数,f(x)称为被插函数。三次样条插值函数对应的曲线称为三次样条插值曲线。
同时我们还可以通过计算三次样条函数 s(x)在节点上的一阶导数 m =s (x )或
二阶导数 M =s (x ),i=0,1,…,n 的值来求过型值点。(x ,y ),i=0,1,…,n 的三
次样条函数。对应地可以导出称之为 m 关系式和关系式,它们分别是关于 m 和 M
的代数方程组。
2.2 三次样条插值算法推导、求解
记 h =x ,i=0,1,…,n-1。根据三次样条函数的定义,当 x [ x ,x ]时,
它是一个三次多项式,所以 s (x)是线性函数,可以表示为:
s (x)= M + M
从 x 到 x 对其积分两次,得
s (x)= - M + M +A
s (x)= M + M + A (x-x )+B
这里 A ,B 是积分常数,可由插值条件,即 s(x )= y ,s(x )=y ,来确定。
4
















