
求用 matlab 编 BP 神经网络预测程序
求一用 matlab 编的程序
P=[。。。];输入 T=[。。。];输出
% 创建一个新的前向神经网络
net_1=newff(minmax(P),[10,1],{'tansig','purelin'},'traingdm')
% 当前输入层权值和阈值
inputWeights=net_1.IW{1,1}
inputbias=net_1.b{1}
% 当前网络层权值和阈值
layerWeights=net_1.LW{2,1}
layerbias=net_1.b{2}
% 设置训练参数
net_1.trainParam.show = 50;
net_1.trainParam.lr = 0.05;
net_1.trainParam.mc = 0.9;
net_1.trainParam.epochs = 10000;
net_1.trainParam.goal = 1e-3;
% 调用 TRAINGDM 算法训练 BP 网络
[net_1,tr]=train(net_1,P,T);
% 对 BP 网络进行仿真
A = sim(net_1,P);
% 计算仿真误差
E = T - A;
MSE=mse(E)
x=[。。。]';%测试
sim(net_1,x)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
不可能啊 我 2009
28
对初学神经网络者的小提示

第二步:掌握如下算法:
2.最小均方误差,这个原理是下面提到的神经网络学习算法的理论核心,
入门者要先看《高等数学》(高等教育出版社,同济大学版)第 8 章的
第十节:“最小二乘法”。
3.在第 2 步的基础上看 Hebb 学习算法、SOM 和 K-近邻算法,上述算
法都是在最小均方误差基础上的改进算法,参考书籍是《神经网络原理》
(机械工业出版社,Simon Haykin 著,中英文都有)、《人工神经网络
与模拟进化计算》(清华大学出版社,阎平凡,张长水著)、《模式分类》
(机械工业出版社, Richard O. Duda 等著,中英文都有)、《神
经网络设计》(机械工业出版社,Martin T. Hargan 等著,中英文都
有)。
4.ART(自适应谐振理论),该算法的最通俗易懂的读物就是《神经网络设
计》(机械工业出版社,Martin T. Hargan 等著,中英文都有)的第 15
和 16 章。若看理论分析较费劲可直接编程实现一下 16.2.7 节的
ART1 算法小节中的算法.
4.BP 算法,初学者若对误差反传的分析过程理解吃力可先跳过理论分
析和证明的内容,直接利用最后的学习规则编个小程序并测试,建议看
《机器学习》(机械工业出版社,Tom M. Mitchell 著,中英文都有)
的第 4 章和《神经网络设计》(机械工业出版社,Martin T. Hargan 等
著,中英文都有)的第 11 章。
BP 神经网络 Matlab 实例(1)
分类:Matlab 实例
采用 Matlab 工具箱函数建立神经网络,对一些基本的神经网络参数进
行了说明,深入了解参考 Matlab 帮助文档。
% 例 1 采用动量梯度下降算法训练 BP 网络。
% 训练样本定义如下:
% 输入矢量为
% p =[-1 -2 3 1
% -1 1 5 -3]
% 目标矢量为 t = [-1 -1 1 1]
close all
clear
clc
% ---------------------------------------------------------------
% NEWFF——生成一个新的前向神经网络,函数格式:
% net = newff(PR,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF)
takes,
% PR -- R x 2 matrix of min and max values for R input
elements

% (对于 R 维输入,PR 是一个 R x 2 的矩阵,每一行是相应输入的边
界值)
% Si -- 第 i 层的维数
% TFi -- 第 i 层的传递函数, default = 'tansig'
% BTF -- 反向传播网络的训练函数, default = 'traingdx'
% BLF -- 反向传播网络的权值/阈值学习函数, default = 'learngdm'
% PF -- 性能函数, default = 'mse'
% ---------------------------------------------------------------
% TRAIN——对 BP 神经网络进行训练,函数格式:
% train(NET,P,T,Pi,Ai,VV,TV),输入参数:
% net -- 所建立的网络
% P -- 网络的输入
% T -- 网络的目标值, default = zeros
% Pi -- 初始输入延迟, default = zeros
% Ai -- 初始网络层延迟, default = zeros
% VV -- 验证向量的结构, default = []
% TV -- 测试向量的结构, default = []
% 返回值:
% net -- 训练之后的网络
% TR -- 训练记录(训练次数及每次训练的误差)
% Y -- 网络输出
% E -- 网络误差
% Pf -- 最终输入延迟
% Af -- 最终网络层延迟
% ---------------------------------------------------------------
% SIM——对 BP 神经网络进行仿真,函数格式:
% [Y,Pf,Af,E,perf] = sim(net,P,PiAi,T)
% 参数与前同。
% ---------------------------------------------------------------
%
% 定义训练样本
% P 为输入矢量
echo on
P=[-1, -2, 3, 1;
-1, 1, 5, -3];
% T 为目标矢量
T=[-1, -1, 1, 1];
% 创建一个新的前向神经网络
net=newff(minmax(P),[3,1],{'tansig','purelin'},'traingdm')
% ---------------------------------------------------------------
% 训练函数:traingdm,功能:以动量 BP 算法修正神经网络的权值
和阈值。
% 它的相关特性包括:
% epochs:训练的次数,默认:100
% goal:误差性能目标值,默认:0
% lr:学习率,默认:0.01

% max_fail:确认样本进行仿真时,最大的失败次数,默认:5
% mc:动量因子,默认:0.9
% min_grad:最小梯度值,默认:1e-10
% show:显示的间隔次数,默认:25
% time:训练的最长时间,默认:inf
% ---------------------------------------------------------------
% 当前输入层权值和阈值
inputWeights=net.IW{1,1}
inputbias=net.b{1}
% 当前网络层权值和阈值
layerWeights=net.LW{2,1}
layerbias=net.b{2}
% 设置网络的训练参数
net.trainParam.show = 50;
net.trainParam.lr = 0.05;
net.trainParam.mc = 0.9;
net.trainParam.epochs = 1000;
net.trainParam.goal = 1e-3;
% 调用 TRAINGDM 算法训练 BP 网络
[net,tr]=train(net,P,T);
% 对 BP 网络进行仿真
A = sim(net,P)
% 计算仿真误差
E = T - A
MSE=mse(E)
echo off
figure;
plot((1:4),T,'-*',(1:4),A,'-o')
1 B P神经网络的原理及算法的基本步骤
理 论上已证 明 ,一个 3层的 B P网络能够实现任意的连续映射 ,
可以任意 精度逼近任何给定的连续函数 。
1. 1 B P神经网络的原理
B P
(
B ack P rop aga tion
)
神经网络通常由具有多个节点的 输入层
(
inp u t laye r
)
、隐含层
(
h idden laye r
)
和多个 或一个输 出节点的输出
层
(
ou tp u t laye r
)
组成 ,其学习过程分为信息的 正向传播过程和误
差的反向传播过程两个阶段 。外部输入 的信号经输入层 、隐含层为
止 。的神经元逐层处理 ,向前传播到输 出层 ,给出结果 。如果在
输出层得不到期望输出 ,则转入逆 向传播过程 ,将实际值与网络输
出之间的误差沿原连接通路 返回 ,通过修改各层神经元的连接权重 ,
减少误差 ,然后再转 入正向传播过程 ,反复迭代 ,直到误差小于给定
的值
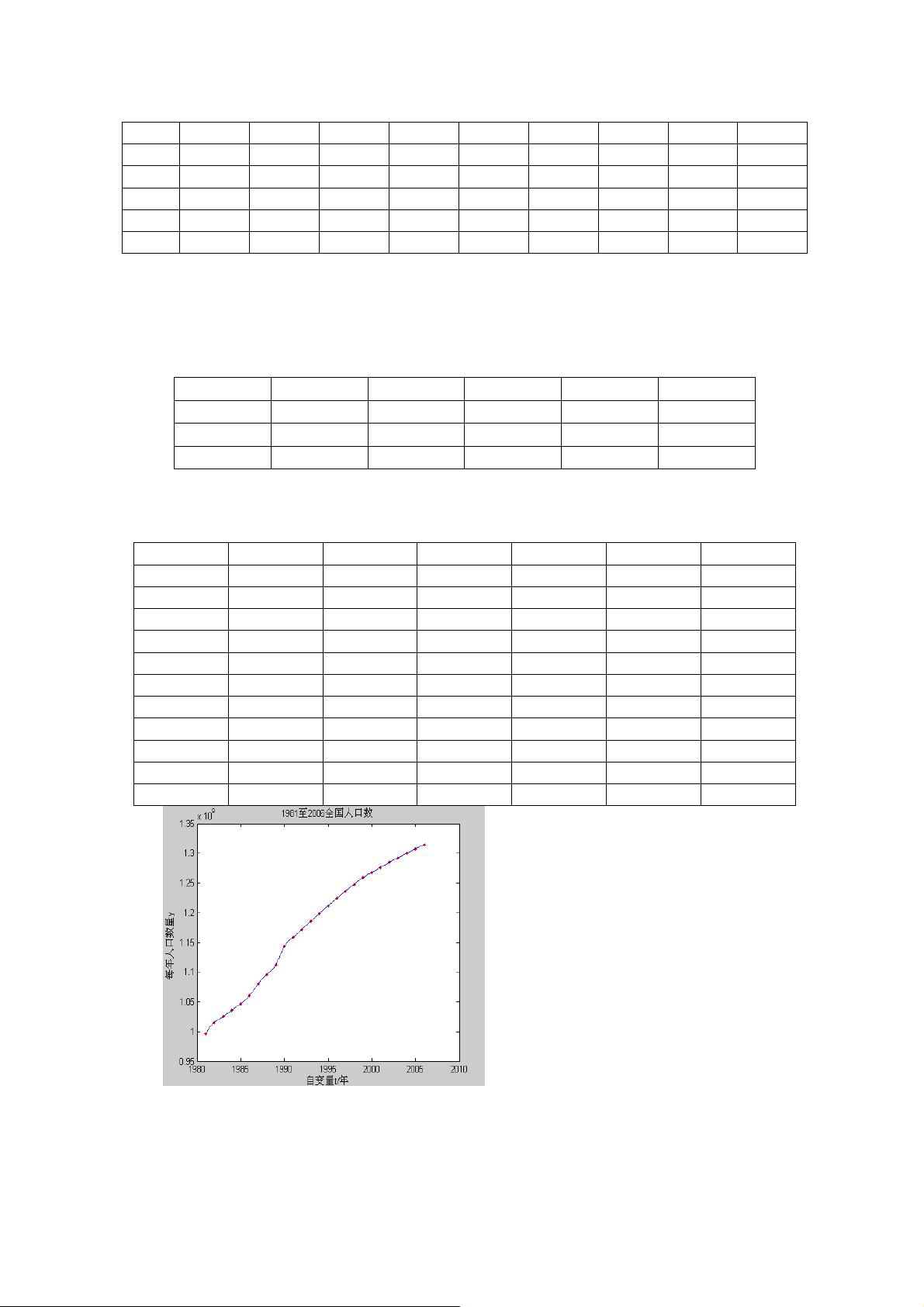
表 1 1981~2005 年全国总人口(单位:万人)
年份
1981
1982
1983
1984
1985
1986
1987
1988
1989
人口
99622
101541
102495
103604
104639
106008
108000
109614
111191
年份
1990
1991
1992
1993
1994
1995
1996
1997
1998
人口
114333
115823
117171
118517
119850
121121
122389
123626
124810
年份
1999
2000
2001
2002
2003
2004
2005
人口
125909
缺省
127627
128453
129227
129988
130756
模型二预测 2001 年~2010 年全国总人口(单位:万人)
年份
2001
2002
2003
2004
2005
人口
127699
128457
129220
129987
130758
年份
2006
2007
2008
2009
2010
人口
131534
132315
133100
133890
134685
模型
���
预测的全国总人口(1981 年至 2016 年)(单位:万人)
年份
1981
1982
1983
1984
1985
1991
人口
99266
101308
102967
104600
106203
115172
年份
1992
1993
1994
1995
2001
2002
人口
116550
117895
119205
120480
127403
128436
年份
2003
2004
2005
2006
2007
2008
人口
129437
130405
131340
132244
133116
133958
年份
2009
2010
2015
2020
2025
2030
人口
134770
135552
139049
141921
144257
146144
年份
2035
2040
2045
2050
2060
2070
人口
147659
148869
149832
150596
151678
152352
年份
2080
2090
2100
2105
2110
2120
人口
152769
153026
153185
153240
153283
153344





















