遗传算法及其MATLAB程序.doc.zip

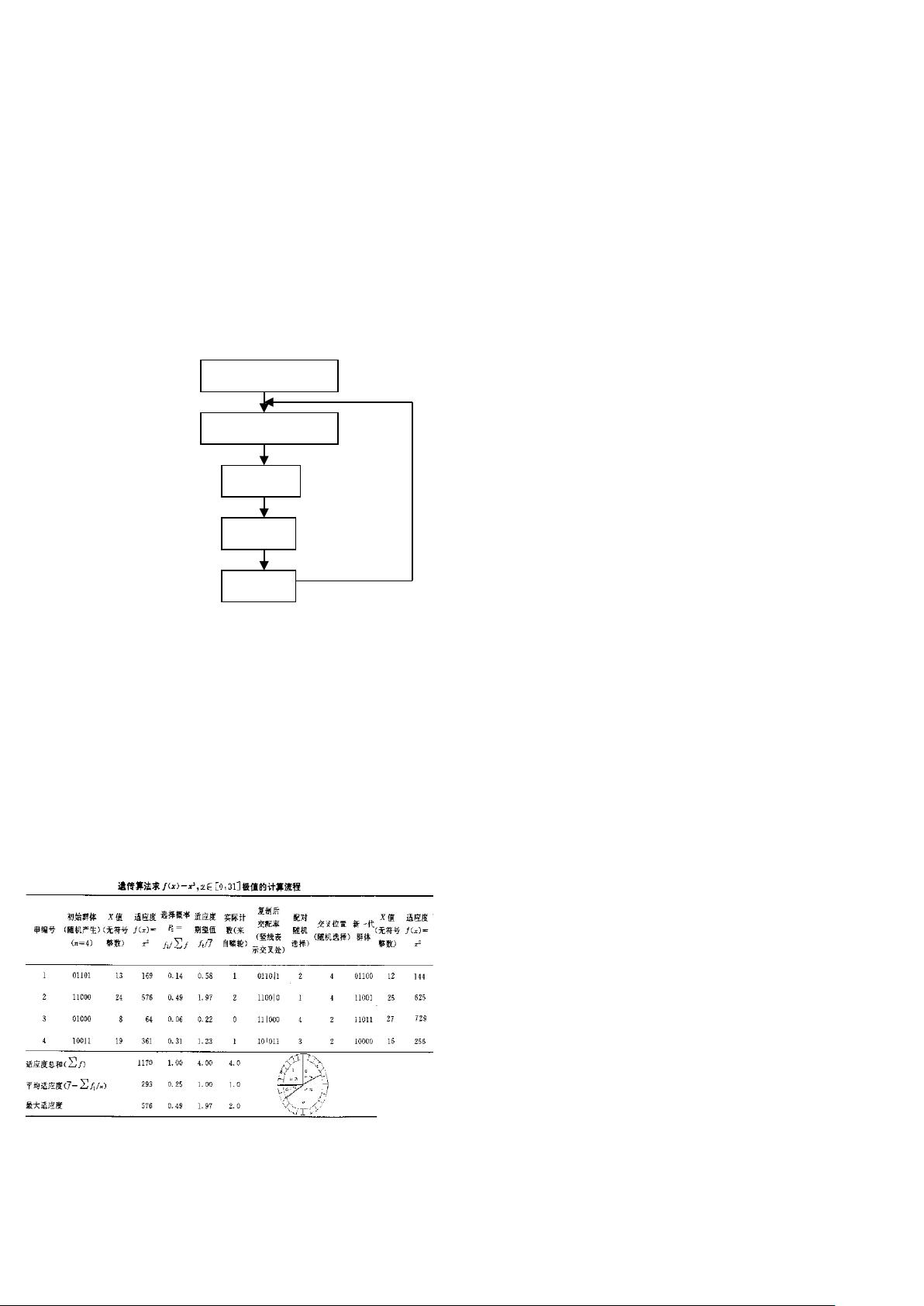
遗传算法是一种模拟生物进化过程的优化方法，由John Henry Holland在20世纪60年代提出。它是计算智能领域的重要组成部分，常用于解决复杂问题的全局优化。这种算法模仿了自然界中的适者生存、遗传和突变等机制，通过迭代过程寻找问题的最优解。 在遗传算法中，首先需要定义一个解决方案的编码方式，这通常被称为个体或染色体。这些个体由一系列基因组成，代表可能的解空间的一部分。例如，在设计问题中，基因可能代表结构参数的值；在旅行商问题中，基因可能表示城市之间的顺序。 算法流程如下： 1. **初始化种群**：随机生成一定数量的初始个体，形成初始种群。 2. **适应度评估**：根据问题的具体目标函数，计算每个个体的适应度值。适应度值越高，代表个体的解质量越好。 3. **选择操作**：依据适应度值进行选择，常用的选择策略有轮盘赌选择、锦标赛选择等。这个步骤确保优秀个体有更大的概率被保留下来。 4. **交叉操作**（Crossover）：选择的个体之间进行配对，通过某种方式交换基因，生成新的个体，模拟生物的遗传过程。常见的交叉操作有单点交叉、多点交叉、均匀交叉等。 5. **变异操作**（Mutation）：对一部分个体进行随机改变，引入新的遗传信息，防止群体过早收敛到局部最优。 6. **替换操作**：新生成的个体替换掉部分旧种群，形成新一代种群。 7. **迭代**：重复上述步骤，直到满足停止条件（如达到最大迭代次数、适应度阈值等）。 MATLAB是一种广泛使用的数学计算和数据分析环境，其强大的矩阵运算能力和丰富的工具箱使其成为实现遗传算法的理想平台。在MATLAB中，可以编写自定义的遗传算法函数，或者利用MATLAB的Global Optimization Toolbox中的内置遗传算法函数`ga`。 编写MATLAB遗传算法程序时，需要定义以下几个关键部分： 1. **编码方案**：定义个体的结构，例如用向量表示染色体。 2. **适应度函数**：定义计算适应度值的函数，返回值越高表示解越优。 3. **选择、交叉和变异函数**：可自定义或使用MATLAB提供的标准函数。 4. **设置参数**：如种群大小、最大迭代次数、交叉概率、变异概率等。 5. **调用`ga`函数**：传入适应度函数、编码方案和其他参数，运行遗传算法。 以下是一个简单的MATLAB遗传算法示例： ```matlab % 定义适应度函数 fitnessFcn = @(x) -x(1)^2 - x(2)^2; % 求最小值，目标函数为-x1^2 - x2^2 % 设置参数 options = gaoptimset('PopulationSize', 50, ... % 种群大小 'Generations', 100, ... % 最大迭代次数 'CrossOverFcn', 'uniform', ... % 交叉函数 'MutationFcn', 'binomial'); % 变异函数 % 初始化问题 lb = [-10; -10]; % 限制下界 ub = [10; 10]; % 限制上界 x0 = lb + (ub - lb).*rand(1, 2); % 随机生成初始解 % 调用ga函数 [x, fval] = ga(fitnessFcn, 2, [], [], [], [], lb, ub, [], options); % 输出最优解和适应度值 fprintf('最优解: (%f, %f)\n', x); fprintf('适应度值: %f\n', -fval); ``` 这个例子是求解二维函数的最小值，遗传算法可以扩展到更高维度和更复杂的优化问题。 遗传算法是一种强大的全局优化工具，通过MATLAB的编程能力，我们可以灵活地应用它来解决各种工程和科学问题。理解和掌握遗传算法及其MATLAB实现对于优化问题的求解具有重要的实践价值。