Matlab重叠相加法.zip

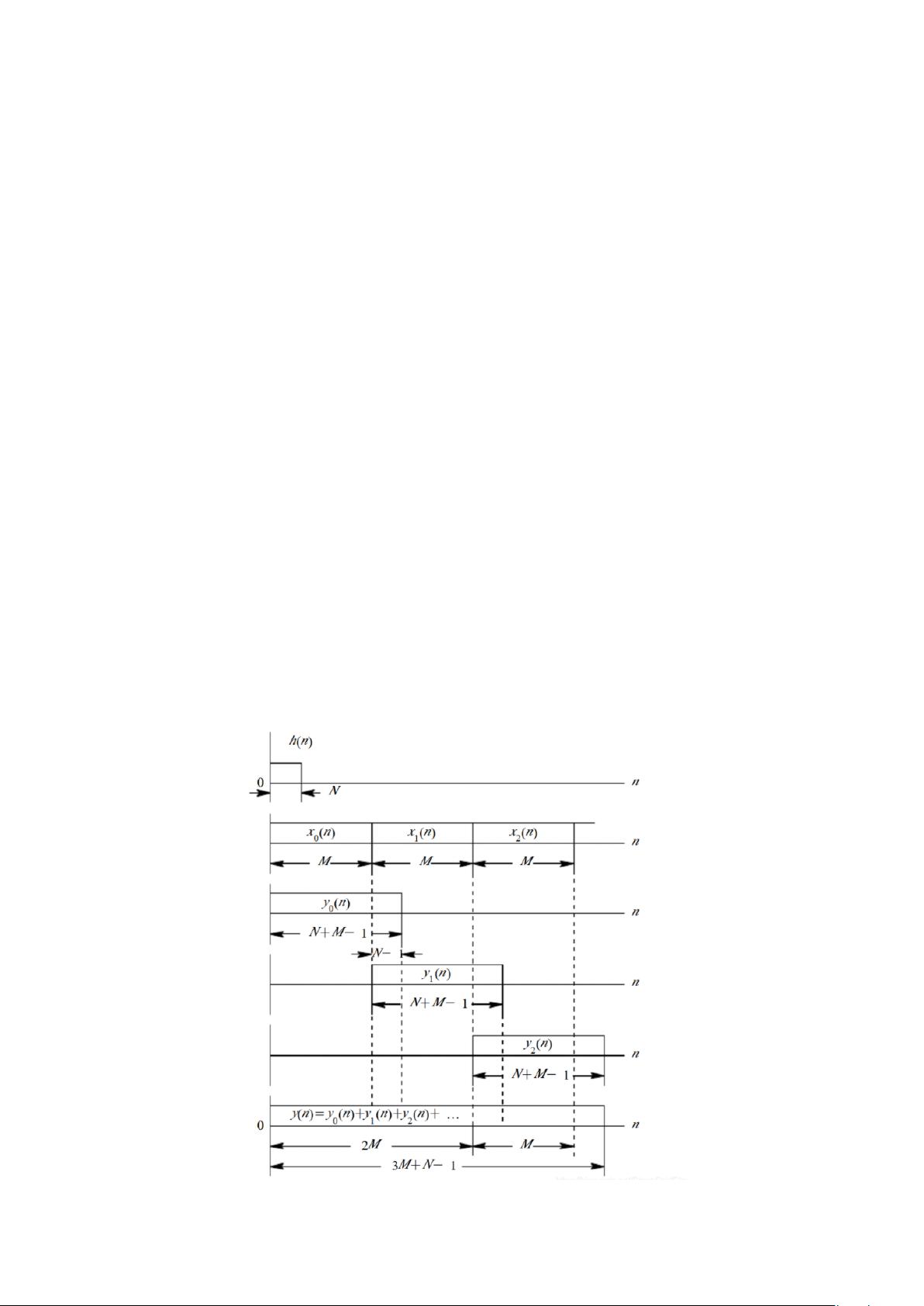
在MATLAB中，重叠相加法（Overlap-Add，OLA）是一种常见的信号处理技术，主要用于连续时间信号的离散表示，特别是在傅立叶变换（FFT）和谱分析中非常有用。它通过将长信号分割成重叠的小段，然后对每一段进行快速傅立叶变换，并将结果相加以重构原始信号。这种方法在处理长序列数据时能够提高计算效率，尤其在音频信号处理、滤波器设计以及多分辨率分析等领域中应用广泛。 理解重叠相加法的基本原理是关键。假设我们有一个长度为N的信号x[n]，我们需要将其分为M段，每段长度为L，重叠部分的长度为W。那么，L必须大于W，通常选择W=L/2，以便在频域有足够的分辨率。对于第k段信号x[kL : (k+1)L-1]，我们可以执行一个N点的FFT，得到X[k]。然后，我们将这M个频谱X[k]相加，但每个频谱在重叠区域需要乘以适当的权重以抵消重复部分的影响。这个权重通常是一个窗函数，例如汉明窗或哈特莱窗，目的是减少边界效应。 接下来，我们将详细解释MATLAB中实现这一过程的步骤： 1. **数据分段**：使用索引来分割信号，例如，对于第一段，可以使用x[1:L]，第二段为x[L+1:2L]，以此类推。 2. **窗函数应用**：在每一段信号上应用窗函数，这可以通过简单的元素乘法完成，比如`win = hamming(L); x_segmented = x .* win;`。 3. **快速傅立叶变换**：对每个分段后的信号执行FFT，如`X_k = fft(x_segmented);`。 4. **相加处理**：将每个频谱X_k在重叠区域乘以权重，然后相加。权重通常是窗函数的逆，即`overlap_weight = hann(W)';`，并乘以窗函数的长度，因为窗函数在重叠部分的值会重复计算。 5. **重构信号**：使用IFFT（逆快速傅立叶变换）将频域的结果转换回时域，`x_reconstructed = ifft(accumarray(fftshift(find(overlap_weight)), X .* overlap_weight, [N 1]));`。`accumarray`函数用于处理重叠部分的累加。 在提供的压缩包文件中，可能包含了一个介绍文章，详细阐述了上述概念和方法，以及可能的实例应用。`a.txt`可能是额外的说明或者代码的注释，而`代码`文件很可能是MATLAB代码示例，展示了如何实际操作这些步骤。 MATLAB中的重叠相加法是一种有效的信号处理工具，它利用了FFT的并行计算能力，减少了计算量，并且通过窗函数的使用改善了频谱分析的精度。理解并熟练掌握这一技术，对于在MATLAB环境中进行高效的数据处理和分析至关重要。