Lecture 07
Hill Climbing(爬山法):梯度下降
Recall from CSPs lecture: simple, general idea
Start wherever
Repeat: move to the best neighboring state
If no neighbors better than current, quit
What’s particularly tricky(难办的) when hill-climbing for multiclass logistic regression(倒退)?
Optimization over a continuous space
Infinitely many neighbors!
How to do this efficiently?
Lecture 08
决策树:ID3、C4.5
• Advantage of attribute-decrease in uncertainty
• Entropy(熵) of Y before you split
• Entropy after split: Weighted by probability of following each branch,
• Information gain is difference:
ID3:
Maximize information gain
C4.5
ID3 tends to split on attributes with more values
Maximize information gain ratio
ID3 步骤:
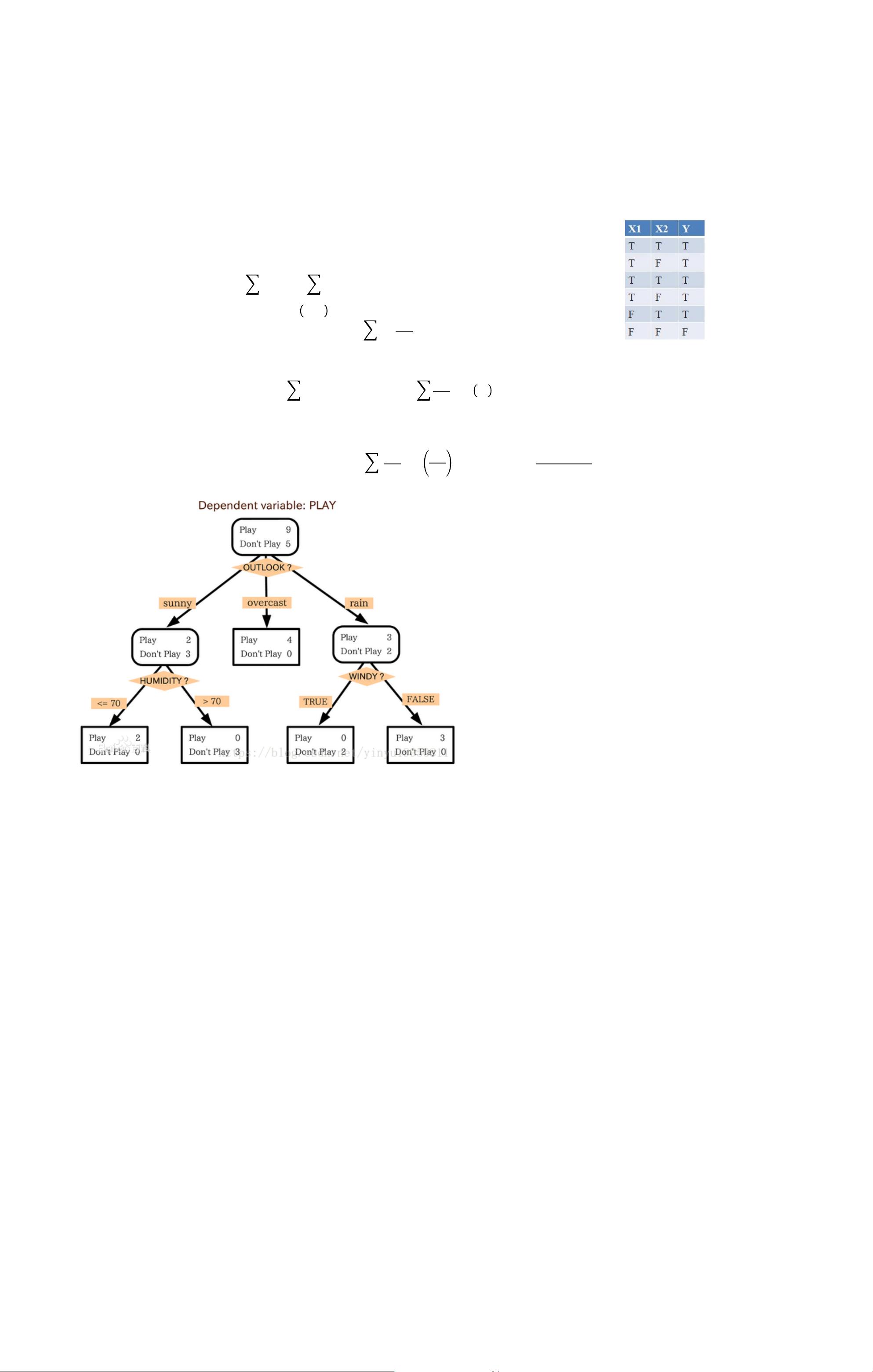
1. Start with a training data set, which we'll call S. It should have attributes(属性) and classifications(类别). The attributes of PlayTennis are outlook,
temperature humidity, and wind, and the classificationis whether or not to play tennis. There are 14 observations.
2. Determine the best attribute in the data set S. The first attribute ID3 picks in our example is outlook. We'll go over the definition of “best attribute” shortly.
3. Split S into subsets that correspond to the possible values of the best attribute. Under outlook, the possible values are sunny, overcast, and rain, so the data is split into
three subsets(rows 1, 2, 8, 9, and 11 for sunny; rows 3, 7, 12, and13 for overcast; and rows 4, 5, 6, 10, and 14 for rain).
4. Make a decision tree node that contains the best attribute. The outlook attribute takes its rightful place at the root of the PlayTennis decision tree.
5. Recursively(递归) make new decision tree nodes with the subsets of data created in step #3. Attributes can't be reused. If a subset of data agrees on the
classification, choose that classification. If there are no more attributes to split on, choose the most popular classification. The sunny data is split further on humidity
because ID3 decides that within the set of sunny rows(1, 2, 8, 9, and 11), humidity is the best attribute.The two paths result in consistent classifications——sunny/high
humidity always leads to no and sunny/normal humidity always leads to yes——so the tree ends after that. The rain data behaves in a similar manner, except with the
wind attribute instead of the humidity attribute. On the other hand, the overcast data always leads to yes without the help of an additional attribute, so the tree ends
immediately.
决策树问题:overfitting(过度拟合)
Overfitting:
When you stop modeling the patterns in the training data (which generalize)
And start modeling the noise (which doesn’t)
如何避免
How can we avoid overfitting?
stop growing when data split not statistically significant
grow full tree, then post-prune(修剪后)
如何控制
Limit the hypothesis(假设) space
E.g. limit the max depth of trees
Easier to analyze
Regularize the hypothesis selection
E.g. chance cutoff
Disprefer most of the hypotheses unless data is clear
Usually done in practice
Lecture 09
Classification from similarity
Case-based(基于实例) reasoning
Predict an instance’s label using similar instances
Nearest-neighbor classification
1-NN: copy the label of the most similar data point
K-NN: vote the k nearest neighbors (need a weighting scheme(方案))
Key issue: how to define similarity
Trade-offs: Small k gives relevant neighbors, Large k gives smoother functions
K-Means(欧氏距离)
An iterative(迭代) clustering algorithm
Pick K random points as cluster centers (means)
Alternate:
Assign data instances to closest mean
Assign each mean to the average of its assigned points