基于双卡尔曼的soc和soh联合估计资源-CSDN文库

共6个文件

pdf：2个

mat：2个

txt：1个

版权申诉

66 浏览量 2023-11-23 14:58:57 上传评论收藏 4.87MB ZIP 举报

标题中的“基于双卡尔曼的soc和soh联合估计”是指使用双卡尔曼滤波算法来同时估计电池的剩余荷电状态（State of Charge, SOC）和健康状态（State of Health, SOH）。SOC是衡量电池当前电量与满电状态之间比例的一个指标，而SOH则是反映电池相对于新电池性能退化的程度。在电动汽车、储能系统等领域，精确估计这两个参数对于电池管理和优化系统性能至关重要。描述中提到的“包括matlab代码以及充放电数据”，意味着提供的资源包含用MATLAB编程语言实现的双卡尔曼滤波算法，以及用于测试和验证算法的电池充放电实验数据。MATLAB是一种广泛使用的数值计算和编程环境，特别适合于信号处理、控制理论和滤波器设计等应用，因此非常适合处理这种类型的问题。双卡尔曼滤波算法是一种扩展的卡尔曼滤波方法，通常用于处理具有多个状态变量和不确定性的动态系统。在这个特定的应用中，它被用来同时估计电池的SOC和SOH，两个状态相互影响，且都受到测量噪声和系统噪声的影响。卡尔曼滤波器通过预测和更新步骤来逐步接近真实的系统状态，同时考虑了系统模型和观测数据的不确定性。在压缩包中，“新建文本文档.txt”可能包含了算法的详细说明、实验设置、数据解释或其他相关文本信息。而“DEKF”可能是“Discrete Extended Kalman Filter”的缩写，即离散扩展卡尔曼滤波器，这是卡尔曼滤波的一种形式，适用于离散时间系统的状态估计，特别是在存在非线性的情况下，如电池模型的非线性特性。具体来说，双卡尔曼滤波过程可能包括以下步骤： 1. 初始化：设定滤波器的初始状态估计和协方差矩阵。 2. 预测：根据电池模型（通常是基于电池的物理特性的数学模型）预测下一时刻的SOC和SOH。 3. 更新：利用实际的充放电数据，校正预测值，得到更准确的SOC和SOH估计。 4. 重复以上步骤，不断迭代，以获得更精确的估计。电池的充放电数据通常包含电流、电压、温度等随时间变化的测量值，这些数据将被用来更新滤波器的状态，并评估算法的性能。通过对不同充放电循环的数据进行处理，可以分析电池性能的变化趋势，从而更好地理解和预测其寿命。这个项目的核心是利用MATLAB实现的双卡尔曼滤波算法，通过对电池充放电数据的处理，实时估计并追踪电池的SOC和SOH，这对于电池管理系统的设计和优化具有重要的实际意义。

资源推荐

资源详情

资源评论

收起资源包目录

DEKF.zip （6个子文件）

新建文本文档.txt 0B

DEKF

参考文献

1-s2.0-S0306261913006284-main.pdf 1.72MB

1-s2.0-S0360544219307595-main.pdf 1.45MB

discharge.mat 2.75MB

DEKF.m 5KB

OCV_SOC.mat 533B

A data-driven multi-scale extended Kalman ﬁltering based parameter

and state estimation approach of lithium-ion polymer battery in electric

vehicles

Rui Xiong

a,b,

⇑

, Fengchun Sun

, Zheng Chen

, Hongwen He

National Engineering Laboratory for Electric Vehicles, School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China

DOE GATE Center for Electric Drive Transportation, Department of Electrical and Computer Engineering, University of Michigan, Dearborn, MI 48128, USA

highlights



A data-driven multi-scale extended Kalman ﬁltering is developed for battery system.



A lumped parameter battery model against different aging levels has been proposed.



The proposed approach has less computation efﬁciency but higher estimation accuracy.



The proposed approach can estimate battery parameter, capacity and SoC concurrently.



The robustness of the proposed approach against different aging levels is evaluated.

article info

Article history:

Received 28 April 2013

Received in revised form 19 July 2013

Accepted 27 July 2013

Available online 23 August 2013

Keywords:

Electric

vehicles

Lithium-ion polymer

battery

Data-driven

State-of-Charge

Battery capacity

Multi-scale

abstract

Accurate estimations of battery parameter and state play an important role in promoting the commer-

cialization of electric vehicles. This paper tries to make three contributions to the existing literatures

through advanced time scale separation algorithm. (1) A lumped parameter battery model was improved

for achieving accurate voltage estimate against different battery aging levels through an electrochemical

equation, which has enhanced the relationship of battery voltage to its State-of-Charge (SoC) and capac-

ity. (2) A multi-scale extended Kalman ﬁltering was proposed and employed to execute the online mea-

sured data driven-based battery parameter and SoC estimation with dual time scales in regarding that the

slow-varying characteristic on battery parameter and fast-varying characteristic on battery SoC, thus the

battery parameter was estimated with macro scale and battery SoC was estimated with micro scale. (3)

The accurate estimate of battery capacity and SoC were obtained in real-time through a data-driven

multi-scale extended Kalman ﬁltering algorithm. Experimental results on various degradation states of

lithium-ion polymer battery cells further veriﬁed the feasibility of the proposed approach.

1. Introduction

To address the two urgent goals nowadays of protecting the

environment and achieving

energy sustainability, it is of strategic

signiﬁcance on a global scale to replace oil-dependent vehicles with

electric vehicles. Battery, as an important on-board electric energy

storage, has been widely used in various electric vehicles. However,

to satisfy the operation voltage and traction power requirements of

electric vehicles, battery packs have to be made up of hundreds

of cells connected in series or parallel to overcome the limitations

of low energy density, low cell capacity and low cell voltage. But

how to avoid the adverse effect of cell inconsistency on battery pack

performanc

e and

prolong the service life of both the pack and the

cells are posing tremendous technological challenges to battery

State-of-Charge (SoC) and capacity estimation techniques. Its

accurate estimation is not only beneﬁcial for the efﬁcient vehicular

energy management, but also for the diagnosis and prognosis of the

battery behavior.

A wide variety of SoC estimation methods have been put forward

to improve battery SoC determination [1–16], each one has its own

advantage. The most commonly used methods fall into two major

categories: the lumped parameter battery model including equiva-

lent circuit models [1–9] and electrochemical model [10] based

SoC estimation method and the ‘‘black box’’ based methods, such

as artiﬁcial neural networks based methods [11–13], fuzzy logic

based methods [14,15] and support vector regression (SVR) based

http://dx.doi.org/10.1016/j.apenergy.2013.07.061

⇑

Corresponding author at: National Engineering Laboratory for Electric Vehicles,

School of Mechanical Engineering, Beijing Institute of Technology, No. 5 South

Zhongguancun Street, Haidian District, Beijing 100081, China. Tel./fax: +86 10 6891

4842.

E-mail addresses: rxiong6@gmail.com, rxiong@ieee.org (R. Xiong).

Applied Energy 113 (2014) 463–476

Contents lists available at ScienceDirect

Applied Energy

journal homepage: www.elsevier.com/locate/apenergy

method [16]. The authors in [1] presented a comparative study of the

equivalent circuit model-based SoC estimation approaches algo-

rithms including Luenberger observer, extended Kalman ﬁltering

(EKF) and sigma point Kalman ﬁltering (SPKF) to monitor the SoC

of a LiFePO

lithium-ion battery (LiB) cell, and the results showed

that the SPKF was an optimal choice to estimate dynamic SoC behav-

ior. The authors in [2–4] presented an equivalent circuit battery

model-based method for real time battery cell SoC estimation using

linear parameter varying (LPV) system and reduced order EKF tech-

niques. Xiong et al. [5,6] proposed an equivalent circuit model based

SoC estimation method using adaptive Extended Kalman Filter

(AEKF) to estimate battery SoC through the measurements of battery

current and voltage. The authors in [10] proposed a reduced order

electrochemical model to estimate internal battery potentials, con-

centration gradients, and SoC from external current and voltage

measurements. The authors in [11] presented a novel approach

using adaptive artiﬁcial neural network and neuron-controller for

online cell SoC determination. The authors in [16] presented v-Sup-

port Vector Regression algorithm based method to estimate the SoC.

A common drawback of the above SoC estimation methods is

that

the model

parameters are identiﬁed with ofﬂine data or the

training data for ‘‘black-box’’ models is built by previously mea-

surement; as a result, the battery model parameters variances fol-

lowing with its degradation and varied operation conditions are

ignored. Thus, the reliability and applicable of these SoC estimators

were not sufﬁciently discussed. In order to overcome these draw-

backs, online parameter identiﬁcation methods were proposed to

track the real-time behavior of the battery. The authors in

[17,18] used the method of recursive least square with an optimal

forgetting factor to carry out the online battery parameters identi-

ﬁcation and state estimation. However, both the model parameters

and capacity are important battery parameters, while the above

method fails to estimate the battery capacity and model parame-

ters concurrently. The reliable capacity estimate is indispensable

for an accurate SoC estimate, and which is of paramount impor-

tance for battery State-of-Health (SoH) indication.

A number of research methods have been proposed for estimat-

ing

the cell

capacity and then to calculate the SoH with the estimated

capacity taking the SoH is the ratio of estimated capacity over its

nominal value, most of them are carried out with lumped parameter

models [5,19–26]. The authors in [19] presented a neural-network

model online estimation method for SoH of valve-regulated lead

acid batteries on the basis of the relationship between the estimated

SoC and the battery open circuit voltage. The authors in [20] pre-

sented a probabilistic neural network (PNN) based SoH estimation

method for LiB, where the PNN was trained using 100 pieces of bat-

teries. The authors in [21] presented an experiment data based SoC

and SoH estimation method with fuzzy logic system, while the

experiment data were provided from electrochemical impedance

spectroscopy (EIS) measurements on new and aged cells. However,

for electric vehicles application, it is not easy to obtain the overall

data for training, which leads to the inaccuracy prediction in com-

plex variable practical application. On the contrary, the dynamic

battery model-based method can provide a cheap alternative in esti-

mation or it can be used along with a sensor-based data-driven

scheme to provide some redundancy. The authors in [22–26] pre-

sented battery model-based dual/joint Kalman ﬁlters method to

estimate the battery SoC and capacity concurrently. However, their

model parameters were identiﬁed by ofﬂine data and the inﬂuence

of the battery degradation or operation conditions over model

parameters are not discussed, as a result, their performance are

not veriﬁed adequately. Furthermore, the authors in [22–25] used

dual EKF or dual SPKF to execute the capacity and SoC joint estima-

tion with one time scale. However, in considering the system param-

eter inclines to change slowly over time while system state is prone

to fast variation over time, it is not an optimal choice to use the same

calculated time scale for battery parameter and state calculation; on

the contrary, it will largely increase the computational burden of

battery

management

system (BMS). Thus the time scale separation

based method, which uses macro scale to calculate the battery

parameter and uses micro scale to calculate the battery state, will

lower the computation cost of BMS. The authors in [26] used the

two time scales to estimate the battery capacity and SoC concur-

rently, and the difference of estimated SoC with dual scales was used

as an innovation to update the Kalman gain to correct the capacity.

But it is very hard to obtain the ‘‘true’’ SoC, thus it is not easy and reli-

able to obtain accurate capacity by the estimated SoC especially

when the estimated SoC is not stable.

The purpose of this paper is to establish general battery param-

eter

and state

dual estimation method using data-driven multi-

scale EKF algorithm, which is a key technique to safeguard the

optimal and safe use of battery – energy source in various electric

vehicles and promote the commercialization of electric vehicles.

The description of the research system and the data-driven mul-

ti-scale EKF algorithm are presented in Section 2. Section 3 de-

scribes the implementation ﬂowchart of the proposed approach.

To evaluate the proposed approach, four different health status of

lithium-ion polymer battery (LiPB) cells are used to carry out the

veriﬁcation are shown in Section 4. The experiment, simulation re-

sults and evaluation of the proposed method are reported in Sec-

tion 5 before conclusions are drawn in Section 6.

2. Data-driven multi-scale extended Kalman ﬁltering

To make the discussion more convenient, ﬁrstly the section con-

structs

a very

general framework for discrete-time lumped dy-

namic system with dual scales. Afterwards, based on the review

of dual EKF, the implementation process of online measured data

driven based multi-scale EKF is built.

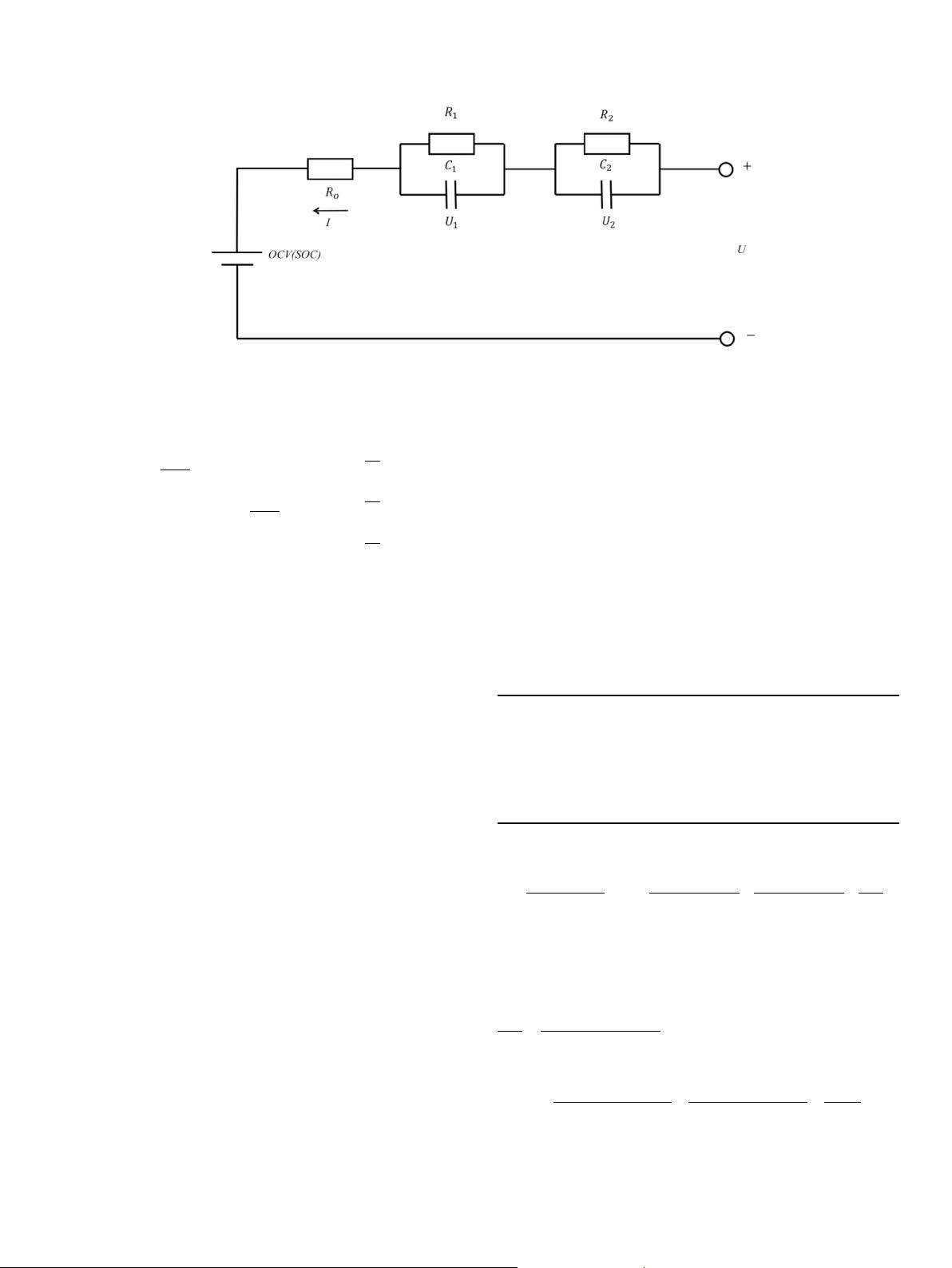
2.1. System description

In regarding that the slow-varying characteristic on battery

paramete

r and

fast-varying characteristic on battery state, we

use multi-scale method to construct the discrete time state-space

equation, where the system parameter and system state are pre-

dicted with the macro and micro scale separately. To be more spe-

ciﬁc, we consider the problem of learning both the hidden states

and parameters h of a very general framework for discrete-time

nonlinear dynamical system as:

k;lþ1

¼ Fð

k;l

; h

; u

k;l

Þþ

k;l

; h

kþ1

¼ h

k;l

¼ Gð

k;l

; h

; u

k;l

Þþ

k;l

(

ð1Þ

where

k,l

is the system state matrix at the time t

k,l

= t

k,0

+l T

(1 6 l 6 L), herein the T is a ﬁxed sampling interval between two adja-

cent measurement points, k and l being the two time-scales indices

for system parameter with macro scale and system state with micro

scale respectively; u

k,l

is the exogenous input matrix at time t

k,l

; y

k,l

the system observation (or measurement) matrix at time t

k,l

;

k,l

and

are the process noise matrix for state and model parameter respec-

tively,

k,l

is the measurement noise matrix. Note that L represents the

level of time-scale separation and that

k,0

k1,L

. h

is the parame-

ters matrix under the kth macro scale, and h

= h

k,0:L1

. With the de-

ﬁned system, we aim at estimating both the system state

and

model parameter h from the noisy observations Y.

2.2. Review of dual EKF method

The EKF provides an efﬁcient approach for generating approxi-

mate maximum-likelihood

estimates of the state of a discrete-time

nonlinear dynamical system. However, the prediction precision of

464 R. Xiong et al. / Applied Energy 113 (2014) 463–476

the EKF largely depends on the predetermined parameter values

used in the system model. Therefore, the dual estimation for the bat-

tery parameter and state is very important. Furthermore, to make

the estimation accuracy of the researched system state more reli-

able, the system parameter is continuously requiring periodic cali-

bration, otherwise the estimation accuracy may be reduced

greatly and even leads to invalid. In other words, when the accurate

system model is not available, a dual estimation approach is re-

quired to achieve reliable and accurate system parameter and state

dual estimation. In this case, the dual EKF, in which both the state of

the dynamical system and parameter are estimated simultaneously,

is proposed to achieve a better prediction precision [25–28].

In this section, we ﬁrstly review the dual EKF algorithm, which

combines

the Kalman

state and parameter ﬁlter. It is noted that its

goal is to predict both the state and model parameter from only

noisy observations. Essentially, two EKF are run concurrently. At

each calculation time, an EKF state ﬁlter-EKF

estimates the state

using the present model estimate h

, while the EKF parameter ﬁl-

ter-EKF

estimates the parameters using the present state estimate

. The system is shown schematically in Fig. 1.

Since the dual EKF does not take into account the time-scale

separation, we use

the notations

to replace

k,l

. In this case,

the measurement is replaced with Y

. It is noted that the system

state matrix



and parameter matrix



are the priori estimates

before the measurement Y

is taken into account; the system state

matrix

and parameter matrix

are the posteriori estimates after

the measurement y

is taken into account.

From Fig. 1, we

ﬁnd that the dual EKF algorithm consists of two

EKF that run concurrently. The top EKF generates state estimate,

and requires



for its time update, thus the ﬁrst step of the dual

EKF operation is time-update for the system parameter, afterwards

the system state is estimated with the



. The bottom EKF gener-

ates parameter estimate, and requires

for the measurement up-

date. The detail numerical formulation of is presented in [28].

2.3. Data-driven multi-scale extended Kalman ﬁltering

To reduce the computation cost of the BMS, a multi-scale EKF

algorithm is proposed

and expected to employ the macro scale to

identify the system parameter of slowly time-varying and employ

the micro scale to estimate the system state of fast time-varying,

and provide more stable estimates of system parameter and state.

The algorithm of the multi-scale EKF for the system described in

Eq. (1) is

summarized in Table

Where h

is the initial system parameter and

is its guess va-

lue;

0,0

is the initial system state and

0;0

is its guess value. The

algorithm is initialized by providing the model parameters and

states to the best guesses based on the prior information, the

covariance matrices are also initialized based on the prior informa-

tion, which is shown in Eq. (2).

Additionally, the computation of C

involves a total derivative of

the measurement function with respect to the parameters as Eq.

(10). In considering that the system state maybe the function of

system parameter, we should decompose the total derivative into

partial derivatives by the following recursive equations.

dGð

k;0

; h; u



h¼



@Gð

k;0

;



; u



@Gð

k;0

;



; u

k;0



k;0



ð11Þ

Then,

k;0



dFð

k1;L1

;



k1;L1



@Fð

k1;L1

;



k1;L1



@Fð

k1;L1

;



k1;L1



ð12Þ

k1;L1



k1;L1

þ K

k1;L1

ðY

k1;L1

 Gð



k1;L1

;



; u

k1;L1

ÞÞÞ ð13Þ



ðK

k1;L1

Þ¼Y

k1;L1



ð14Þ



k1;L1

Gð



k1;L1

;



; u

k1;L1



¼ K

k1;L1

dGð



k1;L1

;



; u

k1;L1



k1;L1



k1;L1

;



; u

k1;L1



ð15Þ

Fig. 1. The dual extended Kalman ﬁlters.

R. Xiong et al. / Applied Energy 113 (2014) 463–476

465

Table 1

Algorithm of multi-scale extended Kalman ﬁltering.

Initialization

¼ E ½h

;

¼ E ðh



Þðh



;

0;0

¼ E ½

0;0

;

0;0

¼ E ½ð

0;0



0;0

Þð

0;0



0;0

ð2Þ

For k

{1, , 1},calculation:

Step 1: Time-update equations for parameters ﬁlter



with macro scale



k1

;

¼

k1

ð3Þ

For l

{1, ..., L}, calculate the state ﬁlter at each micro scale

Step 2: Time-update equations for state



k;l

with micro scale



k1;l

¼ Fð

k1;l1

;



; u

k;l1

Þ;

k1;l

¼A

k1;l1

ð4Þ

Step 3: Measurement-update equations for state

k;l

with micro scale

k1;l

ðC

k1;l

ðC

k1;l



k1;l

þ K

k1;l

½Y

k;l

 Gð



k1;l

;



; u

k1;l

Þ

k1;l

¼ðI  K

k1;l



ð5Þ

Step 4: For time-series calculation l =1:L (l ? L)



k1;L

¼ Fð

k1;L1

;



; u

k1;L1

Þ;

k1;L

¼A

k1;L1

k1;L

k1;l

ðC

k1;L

½C

k1;L

ðC

k1;L



k1;L



k1;L

þ K

k1;L

½Y

k;L

 Gð



k1;L

;



; u

k1;L

Þ

k1;L

¼ðI  K

k1;L



ð6Þ

Step 5: Time scale transform

k;0

k1;L

;

k;0

k1;L

; y

k;0

¼ y

k1;L

; u

k;0

¼ u

k1;L

ð7Þ

For k

{1, ... , 1}, calculation:

Step 6: Measurement-update equations for state ﬁlter

with macro scale

ðC

½C

ðC





þ K

½Y

k;0

 Gð

k;0

;



; u

k;0

Þ

¼ðI  K



ð8Þ

where

k1;l1

@Fð

;



; u

k1;l1

:; C

k1;l

@Gð

;



; u

k1;l



k1;l

ð9Þ

dGð

k;0

; h; u

k;0

h¼



ð10Þ

466 R. Xiong et al. / Applied Energy 113 (2014) 463–476

3. Application to battery system

Section 3.1 presents the discrete-

time cell dynamic model used

in this study. Section 3.2 presents the implementation ﬂowchart of

the proposed approach.

3.1. Lumped parameter battery model

In order to execute the parameter and system estimation with

multi-scale

EKF algorithm,

we need a ‘‘discrete-time cell dynamic

model’’ that relates the battery parameter and SoC to its voltage.

As shown in Fig. 2, it is very important to correctly identify the

model parameter, including the open circuit voltage (OCV) which

is used to describe the voltage source, series resistance (R

) which

is used to describe the electrical resistance of various battery com-

ponents or with the accumulation and dissipation of charge in the

electrical double layer, diffusion resistance (R

Diff

) and diffusion

capacitance (C

Diff

) which consist of a RC network to describe the

mass transport effects and dynamic voltage performances.

Where i

is the load current (assumed positive for discharge,

negative for charge), U

is the terminal voltage, U

describes the

diffusion voltage over the RC network. The battery OCV is replaced

with g(z, Q) in this study, which describes the OCV under different

aging levels and SoCs. Where the z is the abbreviation for battery

SoC, Q denotes the present maximum available capacity of the LiPB

cell. It is noted that the relationship of battery SoC and capacity

with its voltage behavior has been enhanced through the g(z, Q),

which is very important for improving the capacity and SoC predic-

tion precision. The electrical behavior of the lumped parameter

university cell model can be expressed as:

¼

Diff

¼ gðz; QÞU

 i

(

ð16Þ

Herein, we use an electrochemical equation to describe the OCV,

which is from [5].

gðz; Q Þ¼K

þ K

z þ K

þ K

=z þ K

lnðzÞþK

lnð1  zÞ

ð17Þ

where K

(i =0,1,..., 6) are seven polynomial coefﬁcients to accu-

rately ﬁt the OCVs under different SoCs and aging levels.

Considering that the slow-varying behavior in model parame-

ter, we assume that the battery is a time-invariant system and

the load current keeps constant at each sampling interval. After-

wards, we can obtain the analytical solution of Eq. (16) as:

ððk þ 1ÞTÞ¼exp 

Diff



ðkTÞ

exp 

Diff



dt 

ðkTÞ

Diff

ð18Þ

Then we can calculate the diffusion voltage by:

ððk þ 1ÞTÞ¼exp 

Diff



ðkTÞ

þ R

Diff

ðkTÞ 1  exp 

Diff



ð19Þ

Afterwards we can rewrite the diffusion voltage with the sys-

tem equation in Eq. (1).

k;l

¼ exp 

Diff



 U

k;l1

þ 1  exp 

Diff



 i

k;l1

Diff

ð20Þ

where U

k;l

is the diffusion voltage U

at time t

k,l

, i

k,l1

is the load cur-

rent at time t

k,l1

On the other hand, the SoC is the equivalent of a fuel gauge for

the battery in electric vehicles. The basis for SoC state-equation is

developed as follows: If z

k,l

= SoC, we know that

k;l

¼ z

0;0



k;l

0;0

ði

ÞÞi

ð21Þ

where z

0,0

is the initial SoC, i

(

) is the cell current at time

, and

(

)) is the Coulombic efﬁciency of the battery [6]. Herein Q is

the cell maximum available capacity and not the cell nominal capac-

ity, the nominal capacity is the maximum total electrical charge that

can be stored in a cell. It is not a function of temperature and aging

level. The maximum available capacity (discharge capacity) is the

product of the nominal discharge current and discharge time with

the nominal current, thus a shorter discharge times mean a lower

discharge capacity. This indicates that the maximum available

capacity is inﬂuenced by the operation condition and aging level

of battery, thus the Q is a function of temperature and aging level.

A discrete-time approximate recurrence may then be written

as:

k;l

¼ z

k;l1



ði

k;l1

Þi

k;l1

ð22Þ

From Eqs. (16), (20), and (22), we can get:

k;l

exp 

Diff



k;l1

1 exp 

Diff



Diff



ði

k;l

ÞT

k;l1

ð23Þ

We then obtain the state transition and measurement equations as:

k;lþ1

¼ Fðv

k;l

Þ¼

exp 

Diff



k;l

1exp 

Diff



Diff



ði

k;l

ÞT

k;l

¼ Gðv

k;l

Þ¼gðz

k;l

ÞU

k;l

R

k;l

ð24Þ

where

k;l

¼ R

Diff

Q½

k;l

¼ U

k;l

¼ i

k;l

ð25Þ

where U

k;l

is the measured battery voltage at time t

k,l

3.2. Implementation ﬂowchart for advanced multi-scale approach

In accordance with the dual EKF based estimation method

shown in Fig. 1,

we intend to build a multi-scale EKF based estima-

tion method and which allows for a separation of time scale in

state and parameter estimation. To be more speciﬁc, we use macro

Fig. 2. Lumped parameter battery model.

R. Xiong et al. / Applied Energy 113 (2014) 463–476

467

评论收藏

内容反馈

版权申诉

手把手教你学AI

粉丝: 9499
资源: 4844

基于双卡尔曼的soc和soh联合估计

基于卡尔曼滤波的soc估计程序

基于扩展卡尔曼神经网络算法估计电池SOC

BatteryManagementSystem_SOCSOH_soh_SOC_SOH估计_UKFSOC_

【滤波估计】基于matlab双卡尔曼滤波SOC和SOH联合估计【Matlab仿真 2335期】.zip

【滤波估计】基于matlab双卡尔曼滤波SOC和SOH联合估计【含Matlab源码 2335期】.mp4

双卡尔曼SOC估计

功率型锂离子电池双无迹卡尔曼滤波算法（DUKF）soc和soh联合估计，估计欧姆内阻，内阻表征SOH matlab代码 DST

基于扩展卡尔曼神经网络算法估计电池SOC.pdf

卡尔曼滤波估测电池SOC_SOC估计_SOC估计_simulinksoc_电池simulink_soc卡尔曼

基于无迹卡尔曼的分布式电动汽车状态估计.pdf

kftry.rar_卡尔曼 估计_卡尔曼 辨识_基于 最小 二乘法 系统辨识_最小二乘法_辨识代码

【滤波估计】双卡尔曼滤波SOC和SOH联合估计【含Matlab仿真 2335期】.zip

基于双卡尔曼滤波算法DEKF锂离子电池荷电状态SOC与健康状态SOH联合估计 算法具有很好的鲁棒性与估计精度 可提供相关方面的参

双扩展卡尔曼滤波(DEKF)下电池的SOC与SOH联合仿真

动力电池SOC和SOH估计.docx

Klaman.zip_Labview 电池_卡尔曼 soc_卡尔曼滤波 soc_卡尔曼滤波SOC_电池SOC

基于方向和距离的扩展卡尔曼状态估计maltba仿真

【赠送您】UKF 电池SOC估计_SOC估计_soc卡尔曼_电池估计_电池SOC估算_电池

卡尔曼滤波估测电池SOC.rar_lithium_估计电池soc_电池估计_锂电池卡尔曼

基于卡尔曼预测估计器的输入加权预测控制算法 (2007年)

等效电路模型-SOC、SOH健康状态估计-多新息-包含完整文献、代码、数据等，EKF-MIUKF，可以直接运行

Dual and Joint EKF for Simultaneous SOC and SOH Estimation

双卡尔曼滤波法估计电动汽车电池健康状态.pdf

锂离子电池的充电状态和健康状态估计 石墨-磷酸铁锂电池的循环寿命模型 该项目的目标是设计一个强大的观测器，可以估计锂离子电池的SOC和SOH 在该项目中，等效电路模型用于电池建模，电流和环境温度作为

运用卡尔曼滤波的电池soc预测

最新资源

kftry.rar_卡尔曼估计_卡尔曼辨识_基于最小二乘法系统辨识_最小二乘法_辨识代码

基于双卡尔曼滤波算法DEKF锂离子电池荷电状态SOC与健康状态SOH联合估计算法具有很好的鲁棒性与估计精度可提供相关方面的参

锂离子电池的充电状态和健康状态估计石墨-磷酸铁锂电池的循环寿命模型该项目的目标是设计一个强大的观测器，可以估计锂离子电池的SOC和SOH 在该项目中，等效电路模型用于电池建模，电流和环境温度作为