
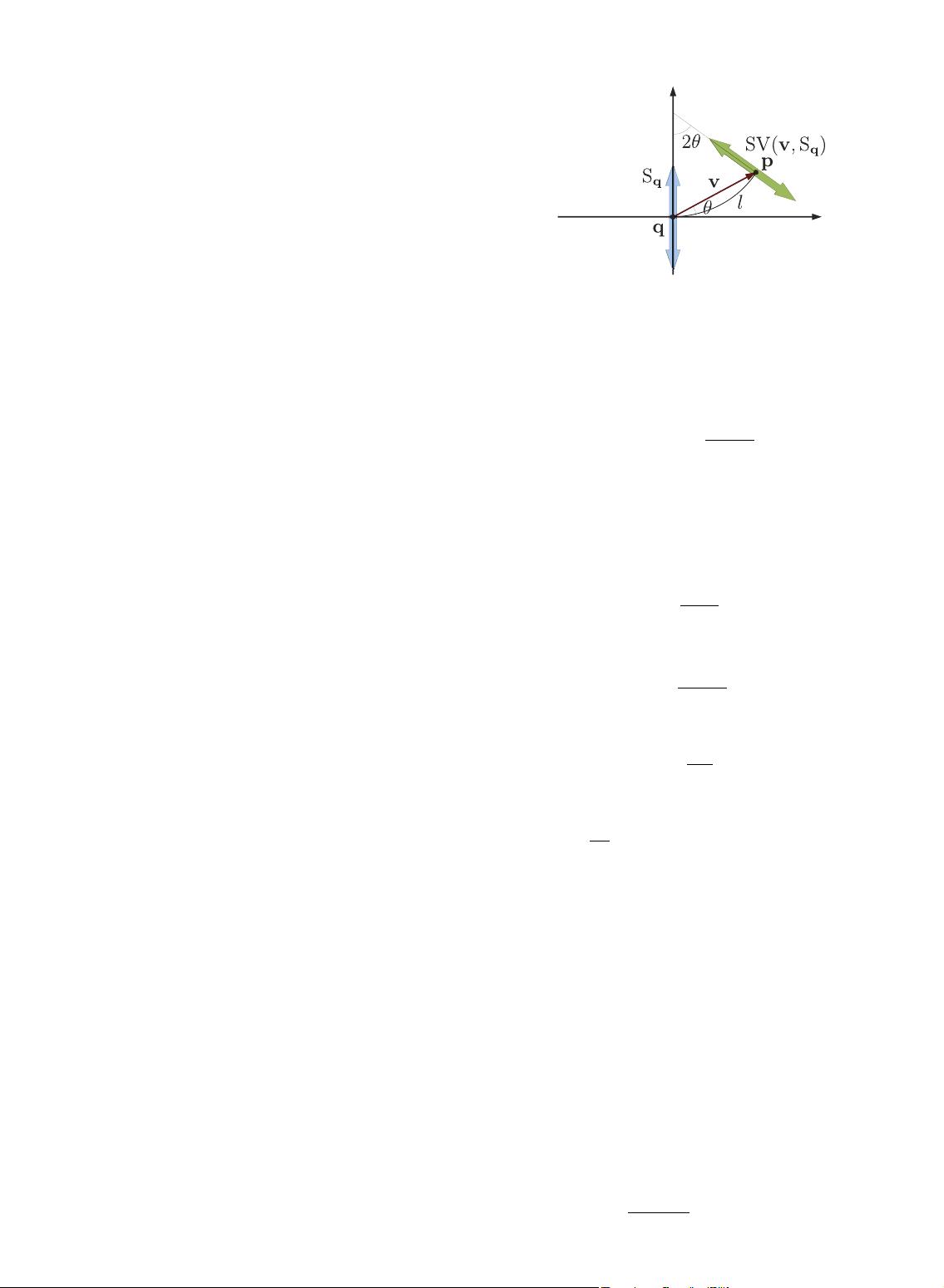
Taking into account that
1
P
¼
2
P
and that S
P
ðÞ is a stick
tensor, the plate vote is defined as the aggregation of stick
votes cast by all the stick tensors S
P
q
ðÞ that constitute P
q
.
Thus, the plate vote is defined as:
PVðv; P
q
Þ¼
1
P
q
Z
2
0
SVðv; S
P
q
ðÞÞd: ð11Þ
2.3 Ball Tensor Voting
Ball tensors are utilized by tensor voting to encode junctions
or noise. Ball tensor voting is defined similarly to plate tensor
voting, that is, in a constructive way. Let S
B
ð; Þbe a unitary
stick tensor oriented in the direction ð1;; Þ in spherical
coordinates. Then, any ball tensor B can be written as:
B ¼
1
B
þ
2
B
þ
3
B
4
Z
S
B
ð; Þd; ð12Þ
where represents the surface of the unitary sphere and
i
B
are the eigenvalues of B. Taking into account that the three
eigenvalues
i
B
are equal and using the same argument as
in the case of plate tensor voting, the ball vote is defined as:
BVðv; B
q
Þ¼
3
1
B
q
4
Z
SVðv; S
B
q
ð; ÞÞd: ð13Þ
3EFFICIENT FORMULATION FOR Plate AND Ball
V
OTES
The evaluation of stick tensor voting is inexpensive since the
rotations involved in that process can be easily avoided by
following the geometric constructions of Fig. 1. Actually,
the complexity of stick tensor voting mainly stems from the
computation of an arcsine required to calculate l and the
exponential required by (9). In addition, these computations
are not necessary for >=4.
Additional efforts have also been made to make stick
tensor voting even more efficient, for example by applying
steerable filters in 2D [6] and tensorial harmonics in 3D in
order to compute stick votes in the frequency domain [7].
Unfortunately, extensions of these methods to calculate
plate and ball votes have not been proposed so far, mainly
due to the difficulty in adapting the integrals in (11) and
(13) to the frequency domain.
On the other hand, computing plate and ball votes is
highly time consumin g since (11) and (13) cannot be
analytically simplified. Thus, researchers usually interpolate
precomputed tensor fields in order to reduce the complexity
of plate and ball tensor voting. Unfortunately, the amount of
precomputed information can grow rapidly if several values
of parameter b are used since the voting fields strongly vary
with it. In addition, the shape of the voting fields also varies
with since (9) is not scale invariant (cf. Section 3.1). In
practice, this fact involves the use of complex systems for
data access and memory management which are not always
available in many applications.
Following a different strategy, [4], [8], and [9] discard
part of the votes for the sake of efficiency. Moreover, [10]
proposed an efficient implementation of tensor voting that
avoids discarding such information through a parallel
implementation on a graphics processing unit (GPU).
However, the improvement is determined by the number
of available processing units. More recently, [11] and [12]
proposed a different weighting factor to be used instead of
(9), which aims at avoiding its discontinuity. The introduc-
tion of this weighting factor simplifies the computations,
but at a cost of yielding very different values from those
obtained through the original tensor voting.
The following sections present a numerical approach to
implement plate and ball votes e fficiently. Instead of
approximating the integrals of (11) and (13), the proposed
approach is based on the scale-invariant version of stick
tensor voting described in the following section.
3.1 Scale-Invariant Stick Tensor Voting
Although the formulation of stick tensor voting given in
Section 2 is inexpensive, it is not scale invariant. Scale
invariance, which can be thought of as invariance under
change of metric units, is a desirable property since the same
results at a particular scale can be obtained for one another
by an appropriate scaling of parameters [13]. This property,
usually followed by physics laws, has been applied to
different fields such as fractal analysis [13], economy [14],
and mathematics [15], among many others. Using scale-
invariant formulations of tensor voting is advantageous. On
the one hand, scale-invariant tensor voting reduces the
complexity of the preprocessing step by only precomputing
voting fields at a single scale, since votes at a different scale
can be interpolat ed from the precomput ed fields by
appropriately scaling spatial distances. On the other hand,
a scale-invariant version of stick tensor voting is essential for
analyzing the properties of plate and ball tensor voting, as
shown in the next sections.
Scale invariance can be defined as follows: Let g be a
function of a set of variables, x, which directly depend on
the spatial length. Function g is scale invariant if [13]:
gðxÞ¼gðh xÞ; for any h 2<: ð14Þ
This definition can be used to check the scale invariance
property of (9). Let us consider s
1s
in (9) as a function of
four variables, namely, l, , , and b. Before checking the
scale invariance of s
1s
, it is necessary to determine the
dependency of each variable on the spatial length. First, l
and directly and inversely depend on the spatial length,
respectively. Second, directly depends on the spatial
length since it is a scale parameter. Finally, b has been
chosen in the literature either as a dimensionless constant
(e.g., [3], [16]) or as a variable that (mainly) depends on the
spatial length (e.g., [17], [4], [8]). It is easy to check that (9) is
not scale invariant under these conditions.
One option to make (9) scale invariant is by making b
dependent on the fourth power of the spatial length, for
instance, with b being proportional to
4
, as proposed in [6].
The main problem with this strategy is the difficulty in
setting the parameters, since both b and determine the
influence of curvature in the votes. This paper describes an
alternative to assure the scale invariance of (9), keeping
intuitive parameter tuning.
In particular, the lack of scale invariance of stick tensor
voting is due to the exponent in (9). From dimensional
analysis [18], that exponent must be dimensionless in order
to assure scale invariance. Thus, (9) can be converted into a
MORENO ET AL.: ON IMPROVING THE EFFICIENCY OF TENSOR VOTING 2217



 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功