分治法大整数乘法课件

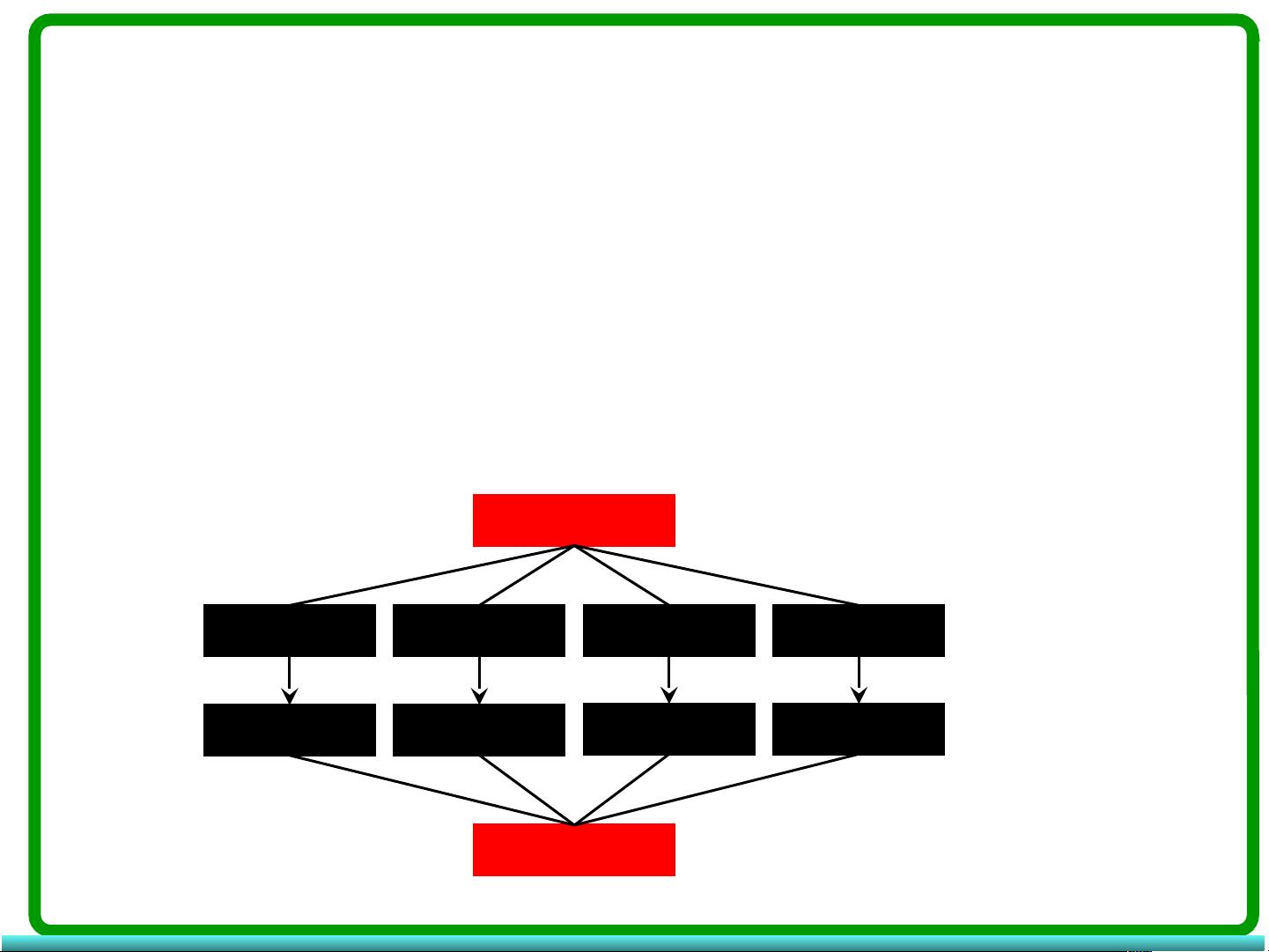
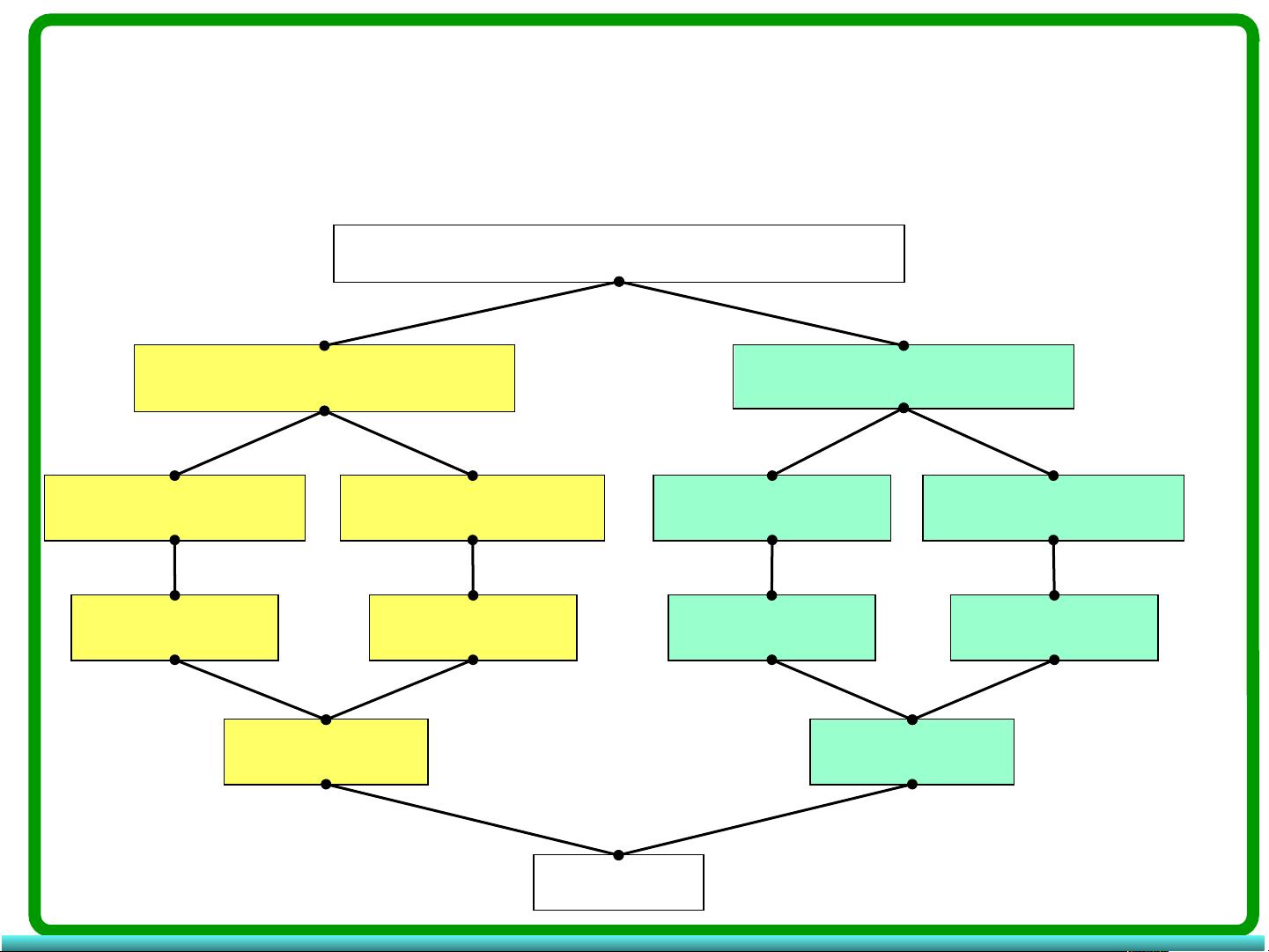
此课件是为了我的博客中写的那篇利用分治法实现大整数乘法而为大家上传的预习课件，感兴趣的朋友可以到我的CSDN博客（http://blog.csdn.net/zhanghua1816）算法设计与分析模块查看完整的利用分治法实现大整数乘法的源代码，希望对你有用！ **分治法大整数乘法** 分治法是一种经典的算法设计策略，它将一个复杂的问题分解成若干个较小的子问题，然后分别解决这些子问题，最后将子问题的解合并得到原问题的解。这种方法特别适用于那些可以通过分解来简化问题结构的问题。 **分治法的基本步骤：** 1. **分解（Divide）**：将原问题分解成若干个规模较小、相互独立、与原问题形式相同的子问题。 2. **求解（Conquer）**：如果子问题足够小，那么可以直接求解，否则递归地对每个子问题进行分治处理。 3. **合并（Combine）**：将子问题的解合并成原问题的解。在某些情况下，合并操作可能是不必要的。 **大整数乘法的应用：** 大整数乘法是分治法的一个典型应用。传统的乘法算法（如竖式乘法）对于非常大的整数可能会非常慢。而分治法可以显著优化这个过程，例如使用Karatsuba算法或Toom-Cook算法。这些算法通过分解大整数，然后对子问题进行乘法运算，最后再组合结果，降低了计算复杂度。 **Karatsuba算法**： - 将两个大整数x和y分解为x = a*2^n + b和y = c*2^n + d，其中a, b, c, d的位数小于n。 - 使用公式x * y = (a + b) * (c + d) - (a * d) - (b * c)计算乘积，避免了传统乘法中的逐位相乘。 - 这个过程可以通过递归持续应用到a, b, c, d上，直到子问题足够小，可以直接计算。 **Toom-Cook算法**： - 类似于Karatsuba，但可以处理更多的子问题，从而可能在某些情况下获得更好的性能。 - 它将两个数分解成更少的项，然后使用多项式乘法来计算乘积。 **分治法的时间效率分析：** 在分治法中，通常关注的是算法的渐进时间复杂度，也就是当输入规模n增加时，所需基本操作的数量的增长速度。例如，对于合并排序，每次分解将问题大小减半，而合并操作的时间复杂度是线性的，因此总的时间复杂度是O(n log n)。 **分治法的优点：** 1. 结构清晰，易于理解和实现。 2. 可以解决复杂问题，特别是那些可以自然分解的问题。 3. 在某些情况下，可以提供最优或接近最优的解决方案。 **分治法的缺点：** 1. 分解和合并操作可能引入额外的开销。 2. 并非所有问题都适合用分治法解决，有些问题的分解可能过于复杂，或者合并过程困难。 3. 递归可能导致大量的函数调用，消耗额外的内存。 总结来说，分治法是一种强大的算法设计工具，尤其适用于大整数乘法等计算密集型任务。通过理解并熟练掌握这种方法，可以有效地解决许多计算机科学中的复杂问题。在实际编程中，结合分治法和其他算法设计策略，往往能产生高效且优雅的解决方案。