平面直角坐标系中动点几何综合.doc

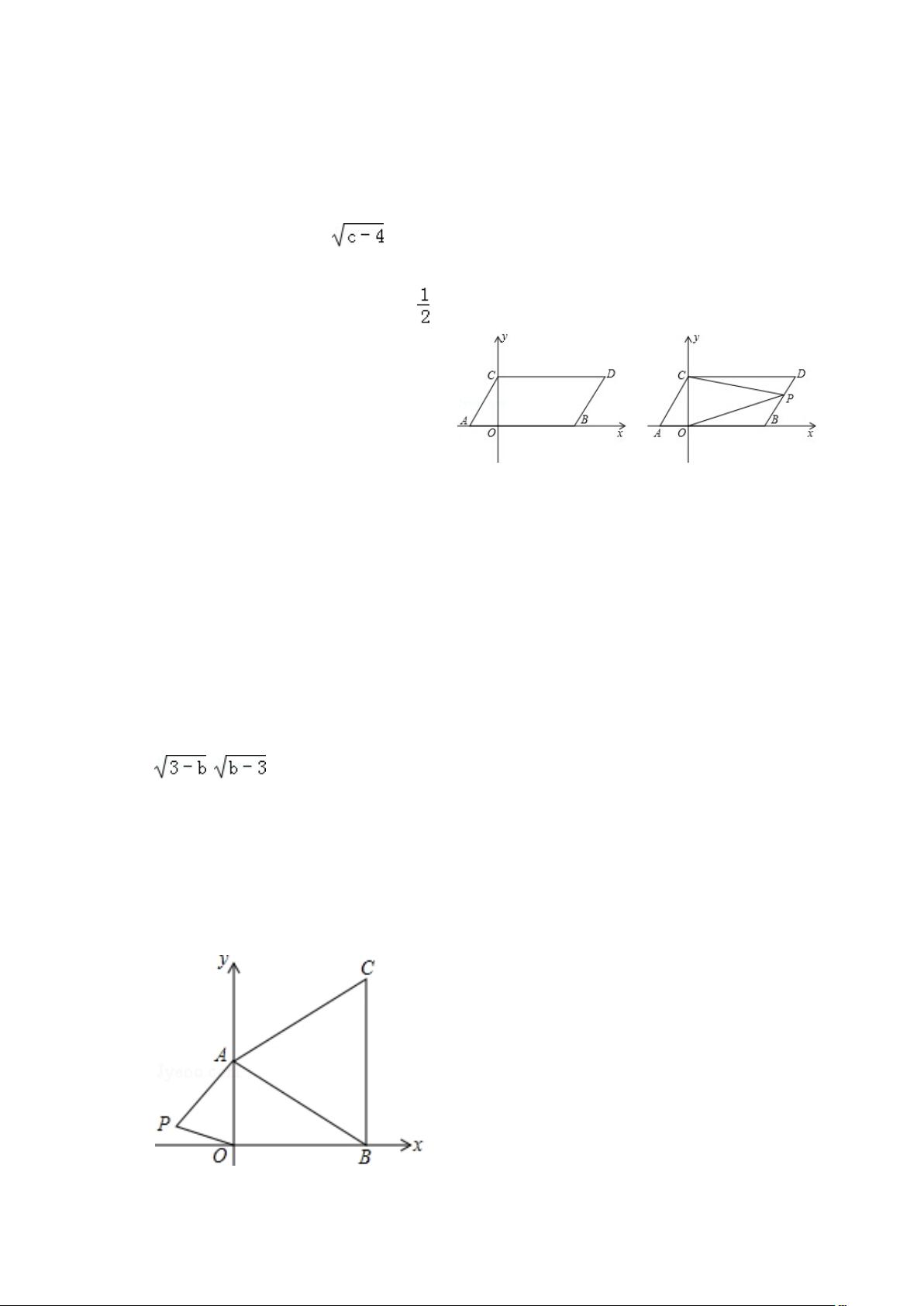
【平面直角坐标系中的动点几何综合】 在平面直角坐标系中，动点问题常常涉及到几何图形的性质、面积计算以及代数关系的综合应用。以下将根据提供的文件内容，逐一解析相关知识点。 1. **绝对值与平方的非负性** 在第一题中，|a - 2| + (b - 3)^2 = 0，这表明a = 2且b = 3。因为绝对值和平方都是非负的，它们之和为0意味着每个项都必须是0。同时，通过点C(3,c)的位置，可以推断c的值。此题考察了绝对值和平方的几何意义，以及如何利用这些性质来确定点的位置。 2. **四边形面积与三角形面积** 第二题涉及到了平移操作，平移不会改变图形的形状和大小。通过给定的线性方程求出点A和B平移后的坐标，然后计算四边形ABDC的面积。接着，假设在y轴上存在点P使得ΔPAB的面积等于四边形ABDC的面积，这需要对点P的坐标进行分析。考虑点P在线段BD上移动时，与PC和PO有关的值是否保持不变。 3. **平行线、相似三角形与角平分线** 第三题中，直线l∥PQ，利用平行线性质可推断出某些角度相等。在证明∠CEF=∠CFE时，可能需要利用到AC⊥BC这一条件。当∠ADC=∠DAC时，考虑∠ACB的平分线的性质，探讨在点B运动过程中某个量是否保持不变。 4. **线段交点、平行线与角平分线** 第四题中，点F是线段AB与y轴的交点，可以通过给定的线性关系确定点A和点B的坐标。进一步，若ED∥AB，AM和DM是∠CAB和∠ODE的平分线，可以求出∠AMD的度数。寻找坐标轴上的点P，使得ΔABP的面积等于ΔABC的面积，这需要对点P的位置进行分析。 5. **三角形面积与坐标几何** 最后一题中，点A、B的坐标满足特定的方程组，通过解这个方程组可以找到点A和点B的坐标。再利用S△ABC=6来确定点C的坐标。对于是否存在点P( t, t)使得S△PAB = S△ABC的问题，需要比较点P和点C的坐标特性。考虑四边形CMDN的特殊性质，如M是AC的中点，N与BN的关系，来确定点D的位置并计算四边形CMDN的面积。 以上知识点涵盖了平面直角坐标系中的几何图形性质、代数方程的解决、动点问题、平移变换、面积计算、三角形的相似和平行线的性质等。在解决这类问题时，需要灵活运用这些知识，结合具体条件进行推理和计算。