动态规划的技巧——阶段的划分和状态的表示

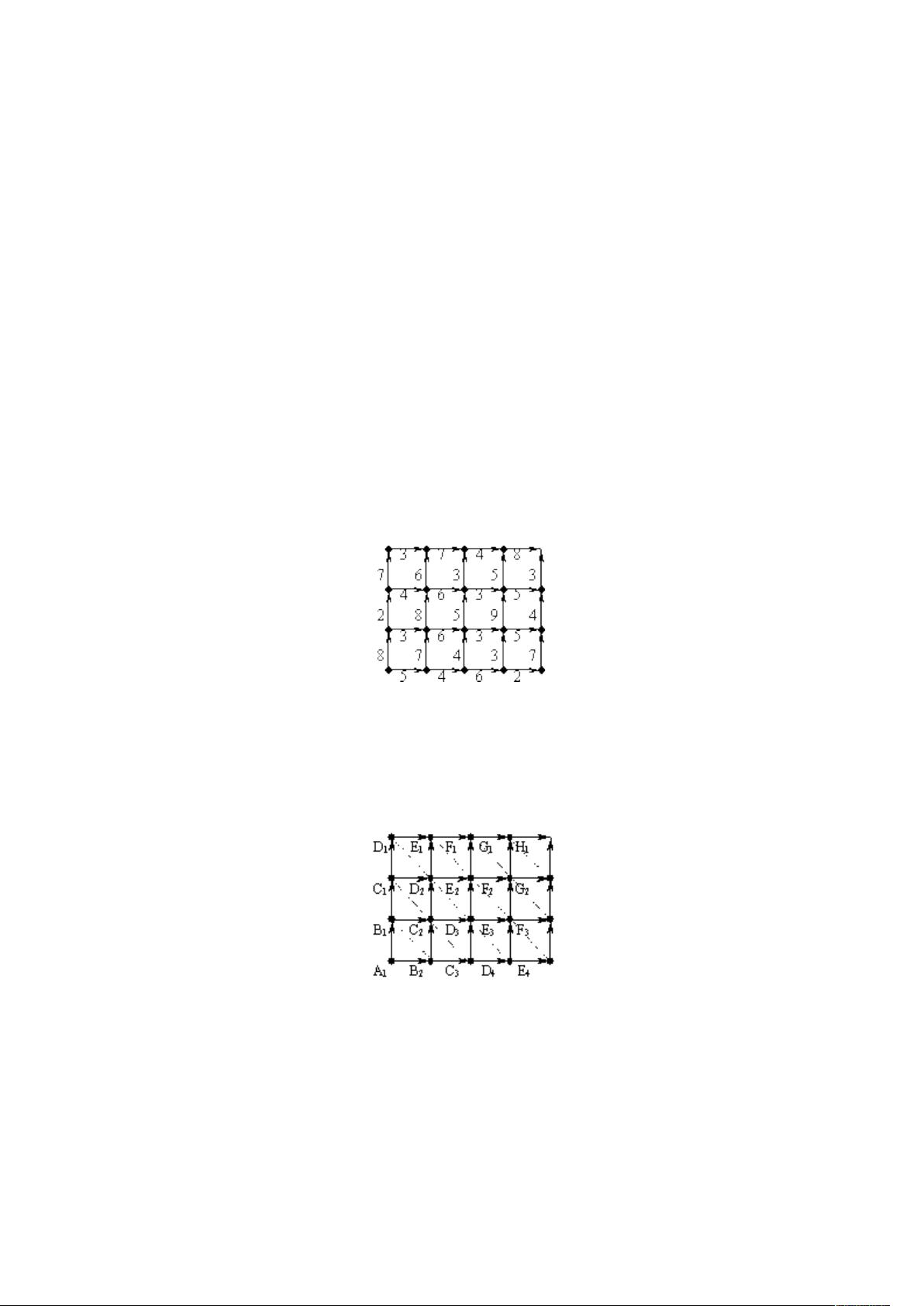
### 动态规划技巧详解：阶段划分与状态表示 #### 引言 动态规划（Dynamic Programming，简称DP）是一种在计算机科学与数学优化领域中广泛使用的算法思想和技术。其核心在于将复杂问题分解为一系列相互关联的小问题，并通过存储这些小问题的解，避免重复计算，从而达到高效求解的目的。在动态规划设计过程中，如何合理地进行**阶段的划分**与**状态的表示**尤为关键，这两个步骤直接关系到问题求解的效率和可行性。 #### 阶段划分的重要性 在动态规划中，阶段划分指的是将原问题按一定的顺序划分为若干个子问题的过程。每个子问题都可以看作是解决问题过程中的一个阶段。合理的阶段划分能够确保问题的分解既符合实际逻辑，又能有效地组织求解过程，避免不必要的计算。 例如，在“街道问题”中，我们需要找到从左下角到右上角的最短路径，每一步只能向右方或上方移动。如果按照走过步数来划分阶段，虽然逻辑清晰，但在实际应用中可能会导致状态转移方程变得复杂，增加算法实现的难度。相比之下，以地图中的行作为阶段进行划分，则更加直观有效，简化了状态转移的过程。 #### 状态表示的关键作用 状态表示是指在动态规划过程中定义各个阶段的“状态”，以便于记录每个阶段的信息。一个好的状态表示应当简洁明了，同时包含解决问题所需的所有必要信息。状态的选择直接决定了动态规划模型的复杂性和求解效率。 继续以“街道问题”为例，如果选择当前处于哪一点作为状态变量，那么就可以很好地表达出当前位置信息，为下一步的决策提供依据。然而，如果状态表示过于复杂或者不恰当，可能会导致状态空间膨胀，增加计算量，甚至使得动态规划法不再适用。 #### 实例分析 ##### 街道问题 在这个问题中，为了寻找最短路径，首先需要确定如何划分阶段以及如何表示状态。一种常见的做法是将阶段定义为走过的步数，状态定义为当前位置。但这种方法在具体实施时可能会遇到困难，因为状态转移方程需要根据不同情况分段讨论，增加了算法的复杂度。另一种更实用的方法是以地图中的行（如A、B、C、D）作为阶段，这样虽然破坏了动态规划的形式化结构，但在实际操作中更为简便。 然而，当问题扩展为寻找两条不重叠的最短路径时，简单的解决方案就不再适用了。此时，如果采用标准的动态规划方法，通过增加一维状态变量来表示两条路径的位置，状态转移时分别考虑两条路径，就能够有效地解决问题。这种方法不仅能够保证路径不重叠，还能保持动态规划的灵活性和效率。 ##### LITTLESHOPOFFLOWERS (IOI’99) 这个问题涉及花店窗户的布置，目标是最优地排列各种不同种类的花朵。假设有一系列的花瓶从左至右排列，每个花瓶具有独特的特性，且花瓶的数量不少于花束的数量。每种花束都有一个唯一的ID号，这个ID号确定了花束在花瓶中的排列顺序。此外，每个花瓶只能放置一束花。 在解决此类问题时，阶段的划分与状态的表示同样至关重要。可以将阶段定义为当前布置到第几个花瓶，状态则可以表示为已布置的花束集合。例如，如果已经布置了编号为1的花束（如azaleas），那么接下来只能布置编号大于1的花束（如begonias或carnations）。通过这种方式，可以确保花束始终按照正确的顺序排列，同时也简化了状态转移的过程。 ### 结论 动态规划作为一种强大的求解工具，在面对复杂的优化问题时表现出色。然而，要想充分发挥其潜力，合理地进行阶段划分和状态表示至关重要。通过上述实例分析可以看出，合适的阶段划分与状态表示不仅能简化问题的解决过程，还能显著提高算法的效率和可行性。因此，在设计动态规划方案时，应充分考虑问题的特点，精心设计阶段与状态，以达到最佳的求解效果。