
第一章 线性规划引论
◇ 学习重点及难点
1 、线性规划问题的建模及图解法 ( 熟练
掌握 )
2 、非标准形 LP 化成标准形 ( 重点 . 后
续内容学习的基础)

第一节 线性规划问题及其数学模型
线性规划概论:
线性规划是研究线性不等式组的理论,
线性规划是研究线性不等式组的理论,
或者说是研究(高维空间中)凸多面体的
或者说是研究(高维空间中)凸多面体的
理论,是线性代数的应用和发展。
理论,是线性代数的应用和发展。
解决两类问题:
1 、如何合理使用有限的人力,物力
和资金,使得收到最好的经济效益。
2 、如何合理使用有限的人力,物力和
资金,以达到最经济的方式,完成生产计
划的要求。

1.1 线性规划问题的实例
例 1.1 资源的合理利用问题
某厂计划在一个生产周期内生产甲,乙两
种产品,要消耗 和 三种资源,已知每件
产品对这三种资源的消耗,这三种资源的现
有数量和每件产品可获得的利润如表 1-1 所
示。问如何安排生产计划,使得即能充分利
用资源,又使总利润最大?
1 2
,A A
3
A

单件 产品
消耗
资源
甲 乙
资源限制
5 2
2 3
1 5
170
100
150
单件利润
10 18
表 1-1
1
A
3
A
2
A
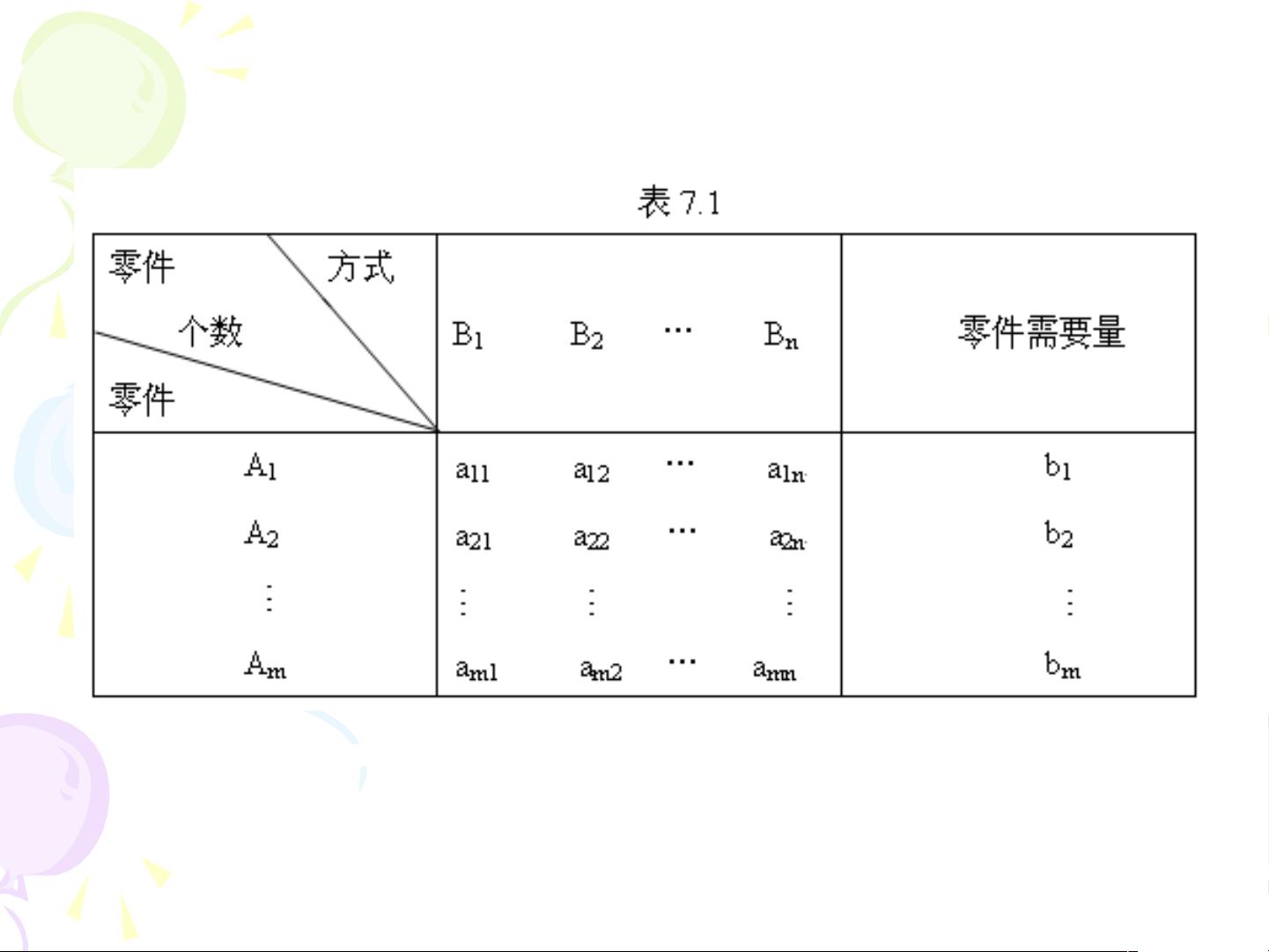
解:将这么一个实际问题转化为线性规划模型,它需要有以下
几个步骤:
1 .确定决策变量: x
1
= 生产甲产品的数量
x
2
= 生产乙产品的数量
2 .确定约束条件:
5x
1
+2x
2
170 ( A
1
资源的限制)
2x
1
+ 3x
2
100 ( A
2
资源的限制)
x
1
+ 5x
2
150 ( A
3
资源的限制)
变量取值限制:
一般情况,决策变量只取正值(非负值)
x
1
0, x
2
0
3 .确定目标函数:工厂的目标是总利润最大
max z=10x
1
+18x
2
















