本文将改进的自适应遗传算法和相结合用于0-1背包问题的求解。此算法对交叉率和变异率进行了优化,实现了交叉率和变异率的非线性自适应调整,并对不可行解进行了贪婪修复。实验结果表明,相比传统的自适应遗传方法,新算法收敛速度快,寻优能力强,具有更可靠的稳定性。 【基于的改进自适应遗传算法】是针对经典的0-1背包问题进行优化求解的一种算法。0-1背包问题是一个著名的组合优化问题,源于实际生活中的多种应用场景,如货物装载、资源分配等。该问题的基本设定是:有n个物品,每个物品有自己的重量w_j和价值v_j,而背包的最大承载重量为b。目标是在不超过背包最大重量的前提下,选择物品使得总价值最大。 传统的遗传算法是一种借鉴生物进化原理的全局优化方法,包括选择、交叉和变异等操作。然而,为了更好地适应0-1背包问题,本文提出了一种改进的自适应遗传算法。该算法主要在两个方面进行了优化: 1. **自适应交叉率和变异率调整**:在传统遗传算法中,交叉率和变异率通常是固定的,而在改进的算法中,它们被设计为非线性自适应调整。这意味着算法可以根据种群的进化状态动态改变这两个参数,从而在探索和开发之间找到更好的平衡,提高了算法的收敛速度和寻优效率。 2. **不可行解的贪婪修复**:在0-1背包问题中,某些解可能超出背包的承载限制,成为不可行解。改进的算法引入了贪婪修复策略,当发现不可行解时,算法会依据某种准则(如价值密度)进行调整,优先移除价值低的物品,确保解的可行性,并尽可能保持总价值最大化。 通过实验对比,改进的自适应遗传算法相较于传统的自适应遗传算法表现出了更快的收敛速度和更强的寻优能力,同时具备更高的稳定性。这表明,针对特定问题的优化策略可以显著提升遗传算法的性能,使之更适合解决实际问题。 此外,贪婪算法作为一种简单的启发式方法,也被用于0-1背包问题的求解。贪婪算法在每次决策时选择当前看起来最优的选项,但不保证全局最优解。相比之下,遗传算法通过种群搜索和遗传操作,能够在全局范围内寻找接近最优的解,特别是在处理大规模和复杂问题时,其优势更为明显。 改进的自适应遗传算法结合了遗传算法的全局优化能力和贪婪算法的局部优化特性,为0-1背包问题提供了一种有效且高效的求解途径。这种方法不仅可以应用于背包问题,还可以推广到其他类似的组合优化问题,展现出广泛的应用潜力。



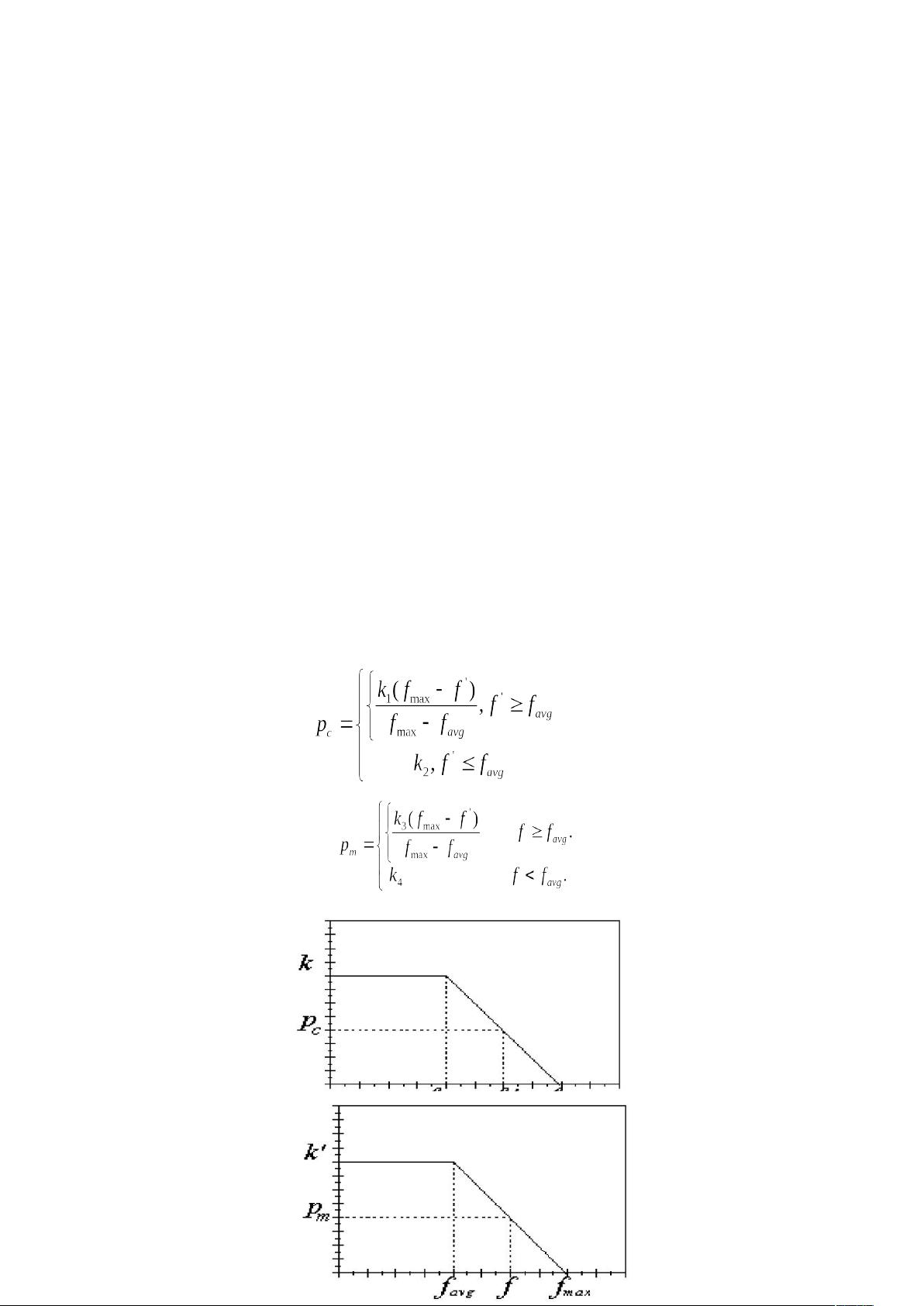

剩余31页未读,继续阅读

 wsfyl2020-04-18随便放了个论文,真坑
wsfyl2020-04-18随便放了个论文,真坑
- 粉丝: 23
- 资源: 2
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功